Знакочередующиеся ряды /qualihelpy

Знакочередующиеся ряды

Справочник / Студент / Ряды /

Справочный материал Примеры Обратите внимание! Видео Модели Пройти тесты

Знакочередующимся рядом называют ряд вида
$LaTeX formula: \sum_{n=1}^{\infty }(-1)^{n-1}a_{n}=a_{1}-a_{2}+a_{3}-a_{4}+...$ , (9.6)
где $LaTeX formula: a_{n}> 0$ .

Например, ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{(-1)^{n-1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-...$ является знакочередующимся.

Признак Лейбница : если 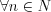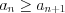$LaTeX formula: \forall n\in N$ $LaTeX formula: a_{n}\geq a_{n+1}$ и $LaTeX formula: \lim_{n \to \infty }a_{n}=0$ , то ряд 9.6 сходится.
Если ряд $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ , составленный из модулей членов ряда 9.6 , сходится, то ряд 9.6 сходится абсолютно .
Если ряд $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ расходится, а ряд 9.6 сходится, то ряд 9.6 сходится условно .

Пример 1 . Исследуйте на абсолютную и условную сходимость ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{(-1)^{n-1}}{n^{2}+1}$ .
Решение . Запишем ряд, составленный из модулей членов данного ряда: $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n^{2}+1}$ . Так как члены ряда положительны и не возрастают, то применим интегральный признак Коши:
$LaTeX formula: \int_{1}^{\infty }\frac{dn}{n^{2}+1}=arctgn\left | _{1}^{\infty }=\lim_{n \to \infty }arctgn-arctg1=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}$ .
Так как ряд, составленный из модулей членов данного ряда, сходится, то данный ряд сходится абсолютно.

Ответ : Ряд сходится абсолютно.

Пример 2. Исследуйте на абсолютную и условную сходимость ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{(-1)^{n-1}}{n}$ .
Решение. Запишем ряд, составленный из модулей членов данного ряда: $LaTeX formula: \sum_{n=1}^{\infty }\frac{1}{n}$ . Получили гармонический ряд, который расходится.
Исследуем на сходимость знакочередующийся ряд $LaTeX formula: \sum_{n=1}^{\infty }\frac{(-1)^{n-1}}{n}$ , где $LaTeX formula: a_{n}=\frac{1}{n}$ , а $LaTeX formula: a_{n+1}=\frac{1}{n+1}$ . Согласно признаку Лейбница этот ряд сходится, так как $LaTeX formula: \frac{1}{n}> \frac{1}{n+1}$ и $LaTeX formula: \lim_{n \to \infty }\frac{1}{n}=0$ .
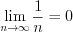Следовательно, данный ряд сходится условно.
Ответ: Ряд сходится условно.

Если ряд $LaTeX formula: \sum_{n=1}^{\infty }a_{n}$ , составленный из модулей членов ряда $LaTeX formula: \sum_{n=1}^{\infty }(-1)^{n-1}a_{n}$ , расходится, то сам ряд $LaTeX formula: \sum_{n=1}^{\infty }(-1)^{n-1}a_{n}$ может сходиться, а может и расходиться.

Программа для просмотра моделей (МК-плеер) Файлы для скачивания

Знакочередующиеся ряды