Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

 1. Площадь криволинейной трапеции (рис. 7.1) можно вычислить по формуле:
1. Площадь криволинейной трапеции (рис. 7.1) можно вычислить по формуле:
 (7.45)
(7.45) (7.46)
(7.46) (7.47)
(7.47) (7.48)
(7.48)



Площадь плоской фигуры
Криволинейной трапецией называют плоскую фигуру, ограниченную графиком непрерывной функции  , где
, где  , отрезками прямых
, отрезками прямых  и
и 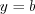 и осью
и осью 
 рис.
рис. 

 , где
, где  , отрезками прямых
, отрезками прямых  и
и 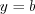 и осью
и осью 
 рис.
рис. 

 (7.45)
(7.45)2. Если криволинейная трапеция ограничена графиком непрерывной функции  , где
, где  , отрезками прямых
, отрезками прямых  и осью
и осью  (рис.
(рис.  ), то ее площадь можно вычислить по формуле:
), то ее площадь можно вычислить по формуле:
 , где
, где  , отрезками прямых
, отрезками прямых  и осью
и осью  (рис.
(рис.  ), то ее площадь можно вычислить по формуле:
), то ее площадь можно вычислить по формуле:  (7.46)
(7.46)3. Если функция  принимает отрицательные значения на отрезке
принимает отрицательные значения на отрезке ![[a;b] LaTeX formula: [a;b]](/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) (рис.
(рис.  ), то площадь фигуры, ограниченной графиком функции
), то площадь фигуры, ограниченной графиком функции  отрезками прямых
отрезками прямых  и
и  можно также вычислить с помощью определенного интеграла. Но так как в этом случае интеграл будет отрицательным, то
можно также вычислить с помощью определенного интеграла. Но так как в этом случае интеграл будет отрицательным, то
 принимает отрицательные значения на отрезке
принимает отрицательные значения на отрезке ![[a;b] LaTeX formula: [a;b]](/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) (рис.
(рис.  ), то площадь фигуры, ограниченной графиком функции
), то площадь фигуры, ограниченной графиком функции  отрезками прямых
отрезками прямых  и
и  можно также вычислить с помощью определенного интеграла. Но так как в этом случае интеграл будет отрицательным, то
можно также вычислить с помощью определенного интеграла. Но так как в этом случае интеграл будет отрицательным, то (7.47)
(7.47)4. Площадь плоской фигуры, ограниченной графиками функций  и отрезками прямых
и отрезками прямых  (рис.
(рис.  ),можно вычислить по формуле:
),можно вычислить по формуле:
 и отрезками прямых
и отрезками прямых  (рис.
(рис.  ),можно вычислить по формуле:
),можно вычислить по формуле: (7.48)
(7.48)5. Площадь плоской фигуры, ограниченной графиками функций  и
и  (рис.
(рис.  ) можно вычислить по формуле 7.48, следуя алгоритму:
) можно вычислить по формуле 7.48, следуя алгоритму:
1) найти абсциссы и
и  точек пересечения графиков функций
точек пересечения графиков функций  и
и  решая уравнение
решая уравнение  ;
;
2) записать пределы интегрирования и
и 
3) составить подынтегральную функцию
4) вычислить интеграл
5) записать
 и
и  (рис.
(рис.  ) можно вычислить по формуле 7.48, следуя алгоритму:
) можно вычислить по формуле 7.48, следуя алгоритму: 1) найти абсциссы
 и
и  точек пересечения графиков функций
точек пересечения графиков функций  и
и  решая уравнение
решая уравнение  ;
; 2) записать пределы интегрирования
 и
и 
3) составить подынтегральную функцию

4) вычислить интеграл

5) записать

Объем тела вращения
1. Объем тела вращения, образованного вращением вокруг оси  криволинейной трапеции, ограниченной графиком непрерывной функции
криволинейной трапеции, ограниченной графиком непрерывной функции  отрезками прямых
отрезками прямых  и
и  можно вычислить по формуле:
можно вычислить по формуле:
 (7.49)
(7.49)
 криволинейной трапеции, ограниченной графиком непрерывной функции
криволинейной трапеции, ограниченной графиком непрерывной функции  отрезками прямых
отрезками прямых  и
и  можно вычислить по формуле:
можно вычислить по формуле:  (7.49)
(7.49)2. Объем тела, полученного в результате вращения вокруг оси  криволинейной трапеции, ограниченной графиком непрерывной функции
криволинейной трапеции, ограниченной графиком непрерывной функции  отрезками прямых
отрезками прямых  и
и  можно вычислить по формуле:
можно вычислить по формуле:
 (7.50)
(7.50)
 криволинейной трапеции, ограниченной графиком непрерывной функции
криволинейной трапеции, ограниченной графиком непрерывной функции  отрезками прямых
отрезками прямых  и
и  можно вычислить по формуле:
можно вычислить по формуле:  (7.50)
(7.50)Длина дуги плоской кривой
1. Длину дуги кривой  где
где  находят по формуле:
находят по формуле:
 (7.51)
(7.51)
 где
где  находят по формуле:
находят по формуле:  (7.51)
(7.51)2. Длину дуги кривой, заданной параметрически  где
где  находят по формуле:
находят по формуле:
 . (7.52)
. (7.52)
 где
где  находят по формуле:
находят по формуле:  . (7.52)
. (7.52)Пример 1. Найдем площадь криволинейной трапеции, ограниченной линиями  и
и
Решение. Так как на отрезке![\left [0;0,5\pi \right ] LaTeX formula: \left [0;0,5\pi \right ]](/uploads/formulas/6084baf289e37de47f3a1589e3a0fa89d85f663a.1.1.png) функция
функция  неотрицательная (рис.
неотрицательная (рис.  ), то согласно формуле 7.45 получим:
), то согласно формуле 7.45 получим:

Ответ:
 и
и
Решение. Так как на отрезке
![\left [0;0,5\pi \right ] LaTeX formula: \left [0;0,5\pi \right ]](/uploads/formulas/6084baf289e37de47f3a1589e3a0fa89d85f663a.1.1.png) функция
функция  неотрицательная (рис.
неотрицательная (рис.  ), то согласно формуле 7.45 получим:
), то согласно формуле 7.45 получим: 
Ответ:


Пример 2. Найдем площадь криволинейной трапеции, ограниченной линиями  и
и 
Решение. Так как на отрезке![\left [\pi ;2\pi \right ] LaTeX formula: \left [\pi ;2\pi \right ]](/uploads/formulas/e23c88a2233cb347ff0eb255e3df98581550cfcb.1.1.png) функция
функция  неположительная (рис.
неположительная (рис.  ), то согласно формуле 7.47 получим:
), то согласно формуле 7.47 получим:


Ответ: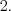
 и
и 
Решение. Так как на отрезке
![\left [\pi ;2\pi \right ] LaTeX formula: \left [\pi ;2\pi \right ]](/uploads/formulas/e23c88a2233cb347ff0eb255e3df98581550cfcb.1.1.png) функция
функция  неположительная (рис.
неположительная (рис.  ), то согласно формуле 7.47 получим:
), то согласно формуле 7.47 получим: 

Ответ:
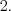
Пример 3. Найдем площадь фигуры, ограниченной линиями  и
и 
Решение. Так как на отрезке![\left [0,25\pi ;\pi \right ] LaTeX formula: \left [0,25\pi ;\pi \right ]](/uploads/formulas/8990150129775595b6cdeea75acb376b0547e705.1.1.png) функция
функция  неотрицательная, а на отрезке
неотрицательная, а на отрезке ![\left [\pi ;1,5\pi \right ] LaTeX formula: \left [\pi ;1,5\pi \right ]](/uploads/formulas/b3aef26129328f5ae85f6077d2f7747d73b33394.1.1.png) она неположительная, то согласно формулам 7.45 и 7.47 получим:
она неположительная, то согласно формулам 7.45 и 7.47 получим:
 .
.
 и
и 
Решение. Так как на отрезке
![\left [0,25\pi ;\pi \right ] LaTeX formula: \left [0,25\pi ;\pi \right ]](/uploads/formulas/8990150129775595b6cdeea75acb376b0547e705.1.1.png) функция
функция  неотрицательная, а на отрезке
неотрицательная, а на отрезке ![\left [\pi ;1,5\pi \right ] LaTeX formula: \left [\pi ;1,5\pi \right ]](/uploads/formulas/b3aef26129328f5ae85f6077d2f7747d73b33394.1.1.png) она неположительная, то согласно формулам 7.45 и 7.47 получим:
она неположительная, то согласно формулам 7.45 и 7.47 получим:  .
.Найдем интегралы:
1) ;
;
1)
 ;
;2)  .
.
Найдем площадь фигуры:
 .
.
Ответ:
 .
. Найдем площадь фигуры:
 .
. Ответ:

Пример 4. Вычислите объем тела, полученного в результате вращения вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  и
и 
Решение. Запишем уравнение гиперболы в виде Согласно формуле 7.50 получим:
Согласно формуле 7.50 получим:

Ответ:
 фигуры, ограниченной линиями
фигуры, ограниченной линиями  и
и 
Решение. Запишем уравнение гиперболы в виде
 Согласно формуле 7.50 получим:
Согласно формуле 7.50 получим: 
Ответ:

Пример 5. Вычислите длину дуги кривой  ограниченную линиями
ограниченную линиями  и
и 
Решение. Составим подынтегральную функцию:
1)
2)
3)
Согласно формуле 7.51 получим:
 .
.
 ограниченную линиями
ограниченную линиями  и
и 
Решение. Составим подынтегральную функцию:
1)

2)

3)

Согласно формуле 7.51 получим:
 .
.Ответ:  .
.
 .
.Если плоская фигура ограничена линиями  и
и  , отрезками прямых
, отрезками прямых  , то ее площадь можно вычислить по формуле:
, то ее площадь можно вычислить по формуле:

 и
и  , отрезками прямых
, отрезками прямых  , то ее площадь можно вычислить по формуле:
, то ее площадь можно вычислить по формуле:

