Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты



где – наибольшая из длин отрезков
– наибольшая из длин отрезков 
 – переменная интегрирования;
– переменная интегрирования;  – нижний,
– нижний,  – верхний пределы интегрирования.
– верхний пределы интегрирования.







 .
.
Применяя табличный интеграл и формулу Ньютона-Лейбница, получим:
и формулу Ньютона-Лейбница, получим:
 .
.
Ответ: .
. ,
,  ,
,  .
.
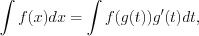 (7.24)
(7.24)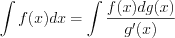 (7.25)
(7.25)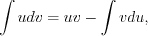 (7.26)
(7.26)
Рассмотрим непрерывную неотрицательную функцию  определенную на некотором отрезке
определенную на некотором отрезке ![[a;b], LaTeX formula: [a;b],](/uploads/formulas/0aa2795f7dda32dca20663c948a8becb27a92741.1.1.png) который разобьем на
который разобьем на  элементарных отрезков длин
элементарных отрезков длин  В каждом из этих отрезков произвольным образом выберем точку
В каждом из этих отрезков произвольным образом выберем точку  (рис. 7.1) и найдем произведения значений функции в этой точке
(рис. 7.1) и найдем произведения значений функции в этой точке  и
и  где
где 
 определенную на некотором отрезке
определенную на некотором отрезке ![[a;b], LaTeX formula: [a;b],](/uploads/formulas/0aa2795f7dda32dca20663c948a8becb27a92741.1.1.png) который разобьем на
который разобьем на  элементарных отрезков длин
элементарных отрезков длин  В каждом из этих отрезков произвольным образом выберем точку
В каждом из этих отрезков произвольным образом выберем точку  (рис. 7.1) и найдем произведения значений функции в этой точке
(рис. 7.1) и найдем произведения значений функции в этой точке  и
и  где
где 
Интегральной суммой называют выражение вида:
 .
. 
 .
. 
Определенным интегралом от функции  называют предел ее интегральной суммы:
называют предел ее интегральной суммы:
 называют предел ее интегральной суммы:
называют предел ее интегральной суммы: 

где
 – наибольшая из длин отрезков
– наибольшая из длин отрезков 
 – переменная интегрирования;
– переменная интегрирования;  – нижний,
– нижний,  – верхний пределы интегрирования.
– верхний пределы интегрирования.Связь между неопределенным и определенным интегралом выражает теорема Ньютона – Лейбница: определенный интеграл от непрерывной функции равен разности значений ее первообразной для верхнего и нижнего предела интегрирования.
Формула Ньютона–Лейбница:
 (7.40)
(7.40)
Формула Ньютона–Лейбница:
 (7.40)
(7.40)Н а п р и м е р,  а
а 
 а
а 
Основные свойства определенного интеграла:








Пример 1. Вычислите интеграл 

 .
. Применяя табличный интеграл
 и формулу Ньютона-Лейбница, получим:
и формулу Ньютона-Лейбница, получим:  .
. Ответ:
 .
.Пример 2. Вычислите интеграл 
Решение. Применим метод подстановки 7.24 и формулу 7.40 .
Полагая получим:
получим: 
Учитывая, что а
а  найдем новые пределы интегрирования:
найдем новые пределы интегрирования:
 ,
,  .
.
Найдем интеграл:
 ,
,  ,
,  ,
,
 ,
,  .
.
Ответ:

Решение. Применим метод подстановки 7.24 и формулу 7.40 .
Полагая
 получим:
получим: 
Учитывая, что
 а
а  найдем новые пределы интегрирования:
найдем новые пределы интегрирования:  ,
,  .
. Найдем интеграл:
 ,
,  ,
,  ,
,  ,
,  .
. Ответ:

Пример 3. Вычислите интеграл  .
.
Решение. Применим формулу интегрирования по частям 7.26 и формулу 7.40 .
 .
. Решение. Применим формулу интегрирования по частям 7.26 и формулу 7.40 .
Положим  а
а  откуда
откуда  ,
,  .
.
Найдем интеграл:
 ,
,  ,
,
 а
а  откуда
откуда  ,
,  .
. Найдем интеграл:
 ,
,  ,
,  ,
,  ,
,  .
.Ответ: 

1. Чтобы вычислить определенный интеграл, необходимо найти соответствующий неопределенный интеграл и применить формулу Ньютона-Лейбница.
2. Методы интегрирования неопределенного и определенного интегралов не различаются.
Подстановка выполняется по формуле:
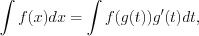 (7.24)
(7.24)где 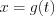 – дифференцируемая функция переменной
– дифференцируемая функция переменной 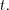
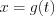 – дифференцируемая функция переменной
– дифференцируемая функция переменной 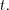
Преобразовать дифференциал можно по формуле:
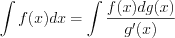 (7.25)
(7.25)Формула интегрирования по частям:
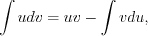 (7.26)
(7.26)где 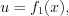 а
а 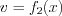 – дифференцируемые функции.
– дифференцируемые функции.
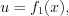 а
а 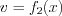 – дифференцируемые функции.
– дифференцируемые функции.Изменение дифференциала


 ,
,