 в данной точке называют предел отношения приращения функции к соответствующему приращению ее аргумента при условии, что последнее стремится к нулю, и записывают:
в данной точке называют предел отношения приращения функции к соответствующему приращению ее аргумента при условии, что последнее стремится к нулю, и записывают:  , (6.1)
, (6.1)где  – приращение функции, а
– приращение функции, а  – приращение ее аргумента в точке
– приращение ее аргумента в точке  ,
, (рис. 6.1).
(рис. 6.1).

Производная функции показывает скорость изменения функции при изменении ее аргумента. Операцию нахождения производной называют дифференцированием .
Производной второго порядка
(второй производной) функции  называют производную ее первой производной и записывают:
называют производную ее первой производной и записывают:  .
.
Аналогично находят производную третьего порядка:  .
.
Производную порядка  записывают:
записывают:  .
.
Геометрический смысл производной
Рассмотрим функцию  и прямую
и прямую 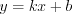 , которая является касательной к графику функции
, которая является касательной к графику функции  и проведена в точке с координатами
и проведена в точке с координатами 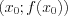 (рис. 6.2).
(рис. 6.2).

Угловой коэффициент  касательной находят по формуле:
касательной находят по формуле:
 или
или  , (6.2)
, (6.2)где  – угол между касательной и положительным направлением оси
– угол между касательной и положительным направлением оси  .
.
Равенство  выражает
геометрический смысл производной.
выражает
геометрический смысл производной.
Дифференциал функции
Дифференциалом  функции
функции  называют произведение ее производной и приращения независимой переменной:
называют произведение ее производной и приращения независимой переменной:
 .
.
Дифференциал функции можно найти по формуле:
 , (6.3)
, (6.3)
где  .
.
Действительно, например, при  , получим:
, получим:  .
.
Геометрический смысл дифференциала
Дифференциал функции равен приращению ординаты касательной к функции в точке, абсцисса которой получает приращение  (рис. 6.3).
(рис. 6.3).

Основные правила дифференцирования
 , где
, где  – число; (6.4)
– число; (6.4) , где
, где  ,
, 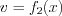 ; (6.5)
; (6.5) ; (6.6)
; (6.6)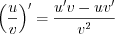 ; (6.7)
; (6.7)  . (6.8)
. (6.8)
Производные элементарных и сложных функций
Таблица производных:

Производная неявной функции
Чтобы найти производную  неявной функции
неявной функции 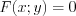 , необходимо дифференцировать обе части равенства
, необходимо дифференцировать обе части равенства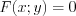 , считая, что
, считая, что  – независимая переменная, а
– независимая переменная, а  – зависимая от
– зависимая от  переменная, и из полученного уравнения выразить явно
переменная, и из полученного уравнения выразить явно  .
.
Производная функции, заданной параметрически
Производную функции  находят по формуле:
находят по формуле:  (6.9)
(6.9)
Производная показательно-степенной функции
Чтобы найти производную показательно-степенной функции  необходимо:
необходимо:
1) прологарифмировать обе части уравнения  :
:
 ;
;
2) согласно свойству логарифмов  записать:
записать:
 ;
;
3) найти производные левой и правой части последнего уравнения:  ,
,  ;
;
4) выразить  явно:
явно: 
 .
. :
:
 .
.Согласно формуле 6.3 найдем дифференциал функции:
 .
. .
.Решение . Применяя правила нахождения производной суммы 6.5 и, используя таблицу производных, получим:
 ,
,  .
. :
:  , откуда
, откуда  .
. ,
,  .
.Решение . 1. Используя таблицу производных найдем:
 ,
,  .
.2. Согласно формуле 6.9 запишем:
 .
. .
.
Решение. 1. Прологарифмируем обе части уравнения: ,
,  .
.
 ,
,  ,
,  .
. 3. Выразим явно
 :
:  .
. Например:
 ,
,  ,
,  .
. 1)
 ;
; 2)
 .
.1) степенной функции
 ;
; 2) показательной функции
 .
.1)
 ;
; 2)  ;
;
3)  .
.

