Раскрытие простейших неопределенностей /qualihelpy

Раскрытие простейших неопределенностей

Справочник / Студент / Пределы /

Справочный материал Примеры Обратите внимание! Видео Модели Пройти тесты

Раскрытие неопределенностей вида $LaTeX formula: \frac{0}{0}$ , $LaTeX formula: \frac{\infty }{\infty }$ , $LaTeX formula: 1^{\infty }$ .

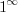1. Раскрытие неопределенности вида $LaTeX formula: \frac{0}{0}$ .

Такая неопределенность может возникнуть при нахождении предела дробно-рациональных функций $LaTeX formula: y=\frac{f(x)}{g(x)}$ при $LaTeX formula: x\rightarrow a$ .

Чтобы раскрыть эту неопределенность, необходимо сократить дробь на критический множитель LaTeX formula: x-a .

Для этого, как правило, необходимо раскладывать числитель и знаменатель дроби на множители.
Разложить многочлены на множители можно различными способами:

1) вынесением общего множителя за скобки;

2) способом группировки;

3) с помощью формул сокращенного умножения:

разности квадратов $LaTeX formula: a^{2}-b^{2}=(a-b)(a+b)$ , (5.21)

квадрата суммы (разности) $LaTeX formula: a^{2}\pm 2ab+b^{2}=(a\pm b)^{2}$ , (5.22)

суммы (разности) кубов $LaTeX formula: a^{3}\pm b^{3}=(a\pm b)(a^{2}\mp ab+b^{2})$ ; (5.23)

4) с помощью формулы разложения квадратного трехчлена на множители:

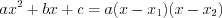$LaTeX formula: ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$ ; (5.24)

3) с помощью деления многочленов уголком.

Если имеем дробно-иррациональную функцию, то предварительно необходимо умножить числитель и знаменатель дроби на выражение, сопряженное выражению, содержащему радикал.

2. Раскрытие неопределенности вида $LaTeX formula: \frac{\infty }{\infty }$ .

Такая неопределенность может возникнуть при нахождении предела дробно-рациональных и дробно-иррациональных функций при $LaTeX formula: x\rightarrow \infty$ .

Чтобы раскрыть эту неопределенность необходимо числитель и знаменатель дроби разделить на высшую степень переменной знаменателя.

3. Замечательные пределы

Первый замечательный предел :

$LaTeX formula: \lim_{x\rightarrow 0}\frac{\sin x}{x}=1$ или $LaTeX formula: \lim_{x\rightarrow 0}\frac{\sin kx}{kx}=1$ (5.25)

Формулу 5.25 применяют при раскрытии неопределенностей вида $LaTeX formula: \frac{0}{0}$ .

Второй замечательный предел: $LaTeX formula: \lim_{x\rightarrow 0}\left ( 1+x \right )^{\frac{1}{x}}=e$

$LaTeX formula: \lim_{x\rightarrow 0}\left ( 1+x \right )^{\frac{1}{x}}=e$ (5.26) или $LaTeX formula: \lim_{x\rightarrow \infty }\left ( 1+\frac{1}{x} \right )^{x}=e$ (5.27)

Формулы 5.26 и 5.27 применяют при раскрытии неопределенностей вида 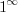$LaTeX formula: 1^{\infty }$ .

Пример 1 . Вычислите $LaTeX formula: \lim_{x\rightarrow 3}\frac{x^{2}-9}{x^{2}-4x+3}$ .

Решение. Так как $LaTeX formula: \lim_{x\rightarrow 3}\frac{x^{2}-9}{x^{2}-4x+3}=\frac{9-9}{9-12+3}=\frac{0}{0}$ , то необходимо сократить дробь на критический множитель LaTeX formula: x-3 .

Для этого разложим числитель и знаменатель дроби на множители.

1) Согласно формуле разности квадратов 5.21 запишем:

$LaTeX formula: x^{2}-9=(x-3)(x+3)$ .

2) Найдем корни квадратного трехчлена, записанного в знаменателе дроби:

LaTeX formula: D=16-12=4 , $LaTeX formula: x_{1}=\frac{4-2}{2}=1$ , $LaTeX formula: x_{2}=\frac{4+2}{2}=3$ .

Согласно формуле 5.24 запишем:

$LaTeX formula: x^{2}-4x+3=(x-1)(x-3)$ .

Вычислим предел:

$LaTeX formula: \lim_{x\rightarrow 3}\frac{(x-3)(x+3)}{(x-1)(x-3)}=\lim_{x\rightarrow 3}\frac{x+3}{x-1}=\frac{3+3}{3-1}=3$ .

Ответ: LaTeX formula: 3 .

Пример 2 . Вычислите $LaTeX formula: \lim_{x\rightarrow 1}\frac{1-\sqrt{x}}{x^{3}-1}$ .

Решение. Так как $LaTeX formula: \lim_{x\rightarrow 1}\frac{1-\sqrt{x}}{x^{3}-1}=\frac{1-\sqrt{1}}{1-1}=\frac{0}{0}$ , то необходимо сократить дробь на критический множитель LaTeX formula: x-1 .

1. Умножим числитель и знаменатель дроби на выражение, сопряженное выражению, записанному в числителе дроби, и применим формулы разности квадратов 5.21 и разности кубов 5.23 :

$LaTeX formula: \lim _{x\rightarrow 1}\frac{(1-\sqrt{x})(1+\sqrt{x})}{(x^{3}-1)(1+\sqrt{x})}=\lim _{x\rightarrow 1}\frac{1-x}{(x-1)(x^{2}+x+1)(1+\sqrt{x})}=$ $LaTeX formula: -\lim _{x\rightarrow 1}\frac{1}{(x^{2}+x+1)(1+\sqrt{x})}=-\frac{1}{6}$ .

Ответ: $LaTeX formula: -\frac{1}{6}$ .

Пример 3 . Вычислите $LaTeX formula: \lim_{x\rightarrow \infty }\frac{3x^{2}-7x}{x^{2}-2}$ .

Решение. Так как имеем неопределенность вида $LaTeX formula: \frac{\infty }{\infty }$ , то разделим числитель и знаменатель дроби на $LaTeX formula: x^{2}$ . Получим:

$LaTeX formula: \lim _{x\rightarrow \infty }\frac{\frac{3x^{2}}{x^{2}}+\frac{7x}{x^{2}}}{\frac{x^{2}}{x^{2}}-\frac{2}{x^{2}}}=\frac{\lim _{x\rightarrow \infty }3+\lim _{x\rightarrow \infty }\frac{7}{x}}{\lim _{x\rightarrow \infty }1-\lim _{x\rightarrow \infty }\frac{2}{x^{2}}}=\frac{3+0}{1-0}=3$ .

Ответ: LaTeX formula: 3 .

Пример 4 . Вычислите $LaTeX formula: \lim_{x\rightarrow 0 }\frac{\sin 5x}{x}$ .

Решение. Имеем неопределенность вида $LaTeX formula: \frac{0}{0}$ .

Умножим числитель и знаменатель дроби на число LaTeX formula: 5 и применим первый замечательный предел 5.25: $LaTeX formula: \lim _{x\rightarrow 0}\frac{5\sin 5x}{5x}=5\lim _{x\rightarrow 0}\frac{\sin 5x}{5x}=5\cdot 1=5$ .

Ответ: LaTeX formula: 5 .

Пример 5 . Вычислите $LaTeX formula: \lim_{x\rightarrow \infty }\left ( \frac{x+3}{x-2} \right )^{x}$ .

Решение. Имеем неопределенность вида 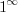$LaTeX formula: 1^{\infty }$ . Чтобы воспользоваться формулой 5.27, выполним преобразования:

$LaTeX formula: \frac{x+3+2-2}{x-2}=\frac{(x-2)+5}{x-2}=\frac{x-2}{x-2}+\frac{5}{x-2}=1+\frac{5}{x-2}$ .

Получим предел: $LaTeX formula: \lim_{x\rightarrow \infty }\left ( 1+\frac{5}{x-2} \right )^{x}$ .

Умножим показатель степени на $LaTeX formula: \frac{5}{x-2}$ и на $LaTeX formula: \frac{x-2}{5}$ :

$LaTeX formula: \lim_{x\rightarrow \infty }\left ( 1+\frac{5}{x-2} \right )^{x\cdot \frac{5}{x-2}\cdot \frac{x-2}{5}}=$ $LaTeX formula: \lim_{x\rightarrow \infty }\left ( \left ( 1+\frac{5}{x-2} \right ) ^{\frac{x-2}{5}}\right )^{\frac{5x}{x-2}}$ $LaTeX formula: =e^{\lim_{x\rightarrow \infty }\frac{5x}{x-2}}$ .

Вычислим предел:

$LaTeX formula: \lim_{x\rightarrow \infty }\frac{5x}{x-2}=\lim_{x\rightarrow \infty }\frac{\frac{5x}{x}}{\frac{x}{x}-\frac{2}{x}}=\lim_{x\rightarrow \infty }\frac{5}{1-\frac{2}{x}}=\frac{5}{1-0}=5$ .