Функцией
 называют такую зависимость переменной
называют такую зависимость переменной  от переменной
от переменной  , при которой каждому допустимому значению
, при которой каждому допустимому значению соответствует
единственное значение
соответствует
единственное значение  .
.
Переменную  называют независимой переменной или
аргументом функции
, а переменную
называют независимой переменной или
аргументом функции
, а переменную  – зависимой от
– зависимой от  переменной или
значением функции .
переменной или
значением функции .
Уравнение  задает функцию
явно
, а уравнение
задает функцию
явно
, а уравнение 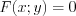 задает функцию
неявно
.
задает функцию
неявно
.
Чтобы задать функцию явно, необходимо в уравнении 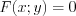 выразить одну переменную через другую.
выразить одну переменную через другую.
Множество всех допустимых значений переменной образуют
область определения
функции.
образуют
область определения
функции.
Область определения функции обозначают  .
.
Множество всех допустимых значений переменной образуют
область значений функции
.
образуют
область значений функции
.
Область значений функции обозначают 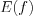 .
.
Н а п р и м е р, область определения функции  составляют числа, принадлежащие промежутку
составляют числа, принадлежащие промежутку  , а область ее значений – числа, принадлежащие промежутку
, а область ее значений – числа, принадлежащие промежутку  .
.
Графиком функции  называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида
называют множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек вида 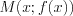 .
.
График функции представляет собой некоторую линию на плоскости.
Функция  возрастает
на промежутке
возрастает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства 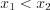 следует неравенство
следует неравенство  (рис. 5.1).
(рис. 5.1).
Функция  убывает
на промежутке
убывает
на промежутке  , если для любых
, если для любых  и
и  , принадлежащих промежутку
, принадлежащих промежутку  , из неравенства
, из неравенства  следует неравенство
следует неравенство 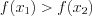 (рис. 5.2).
(рис. 5.2).
Функция называется монотонной
, если она либо только возрастает, либо только убывает на 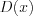 .
.

Говорят, что числовое множество симметрично
относительно точки 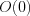 (начала отсчета) координатной прямой, если оно содержит только противоположные элементы.
(начала отсчета) координатной прямой, если оно содержит только противоположные элементы.
Например, числовые множества 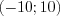 ,
, 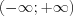 ,
,![[-3;+3] LaTeX formula: [-3;+3]](/uploads/formulas/688cc7f72274e74d5d7338263a07cfdb1573cb36.1.1.png) – симметричные, а множества
– симметричные, а множества 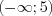 ,
,  и
и 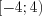 – не симметричные.
– не симметричные.
Функция
называется
четной
, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и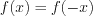 . График четной функции симметричен относительно оси
. График четной функции симметричен относительно оси  .
.
Функция
называется
нечетной
, если  – симметричное множество относительно начала отсчета и
– симметричное множество относительно начала отсчета и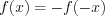 . График нечетной функции симметричен относительно точки
. График нечетной функции симметричен относительно точки  .
.
Функция  называется периодической
, если существует такое число
называется периодической
, если существует такое число 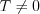 , при котором для всех
, при котором для всех  из области определения функции выполняется равенство
из области определения функции выполняется равенство 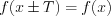 .
.
Н а п р и м е р, тригонометрические функции 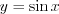 ,
, 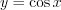 ,
, 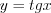 и
и 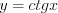 являются периодическими, так как выполняются равенства:
являются периодическими, так как выполняются равенства:
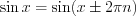 ,
,  ,
,  и
и  , где
, где  .
.
Чтобы построить график периодической функции, достаточно построить ее график на основном (наименьшем) периоде  и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо.
и выполнить параллельный перенос этого графика вдоль оси абсцисс на любое количество периодов влево и вправо.
Н а п р и м е р, рассмотрим функцию  . Запись
. Запись ![[x] LaTeX formula: [x]](/uploads/formulas/3c345a8aed30f94cb97f496efca2e4209abad676.1.1.png) обозначает наибольшую целую часть некоторого числа, не превосходящую это число, а запись
обозначает наибольшую целую часть некоторого числа, не превосходящую это число, а запись  обозначает его дробную часть.
обозначает его дробную часть.
Так, например, ![[5]=5 LaTeX formula: [5]=5](/uploads/formulas/fe8313b11ff96c0631a805d611ce610f68ef1323.1.1.png) ,
, ,
, ![[5,2]=5 LaTeX formula: [5,2]=5](/uploads/formulas/b38d2566f98ec709ac7dd5e2d8fdc1a0527d022c.1.1.png) ,
,  ,
, ![[-5,2]=-6 LaTeX formula: [-5,2]=-6](/uploads/formulas/76dbdf9284e376ef10025276768ea473fb6dcc68.1.1.png) ,
,  .
.
Тогда функция  является периодической с основным периодом, равным
является периодической с основным периодом, равным  .
.
На рисунке 5.3 построен график этой функции на ее основном периоде  , а на рисунке 5.4 построен график этой функции на нескольких периодах.
, а на рисунке 5.4 построен график этой функции на нескольких периодах.

Точки пересечения графика функции с осью абсцисс называют нулями функции.
Чтобы найти нули функции  необходимо решить уравнение
необходимо решить уравнение  .
.
Функция  обратима
, т. е. имеет обратную функцию
обратима
, т. е. имеет обратную функцию 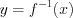 , если она или монотонно возрастает или монотонно убывает на всей своей области определения.
, если она или монотонно возрастает или монотонно убывает на всей своей области определения.
Функции  и
и 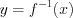 образуют пару взаимно обратных функций.
образуют пару взаимно обратных функций.
Взаимно обратные функции обладают следующими свойствами :
1) область определения функции  является областью значений функции
является областью значений функции 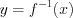 , а область значений функции
, а область значений функции  является областью определения функции
является областью определения функции 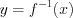 , т.е.
, т.е. 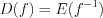 ,
, 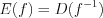 ;
;
2) если функция  монотонно возрастает (убывает), то и функция
монотонно возрастает (убывает), то и функция 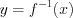 возрастает (убывает);
возрастает (убывает);
3) графики взаимно обратных функций симметричны относительно прямой 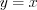 .
.
Чтобы найти функцию обратную функции  необходимо решить уравнение относительно переменной
необходимо решить уравнение относительно переменной  и в этом уравнении заменить
и в этом уравнении заменить  на
на  , а
, а  заменить на
заменить на  .
.
Рассмотрим две функции  и
и  . Функцию вида
. Функцию вида  называют
сложной функцией
.
называют
сложной функцией
.
Н а п р и м е р, если ![y=\sqrt[3]{z} LaTeX formula: y=\sqrt[3]{z}](/uploads/formulas/eb9f120857741f922aeb5339ee26436014286970.1.1.png) , а
, а  , то
, то ![f(x)=\sqrt[3]{(x+4)^{5}} LaTeX formula: f(x)=\sqrt[3]{(x+4)^{5}}](/uploads/formulas/465d62d6680ffd2f8ee2297598b9bfa5624d6855.1.1.png) .
.
 .
.  через переменную
через переменную  , получим:
, получим: ,
,  ,
, ![y=\sqrt[3]{0,5-2x} LaTeX formula: y=\sqrt[3]{0,5-2x}](/uploads/formulas/62abe5450dcce86dcff7062b4887ed3cc13a4beb.1.1.png) .
.![y=\sqrt[3]{0,5-2x} LaTeX formula: y=\sqrt[3]{0,5-2x}](https://helpy.quali.me/uploads/formulas/62abe5450dcce86dcff7062b4887ed3cc13a4beb.1.1.png) .
. 1)
 ; 2)
; 2)  ; 3)
; 3)  .
.1. Функция
 четная, так как:
четная, так как: 1)
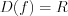 – симметричное множество относительно начала отсчета;
– симметричное множество относительно начала отсчета; 2)
 .
.  нечетная, так как:
нечетная, так как: 1)
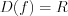 – симметричное множество относительно начала отсчета;
– симметричное множество относительно начала отсчета;2)
 .
.  не является четной и не является нечетной (общего вида), так как:
не является четной и не является нечетной (общего вида), так как:1)
 – не симметричное множество относительно начала отсчета.
– не симметричное множество относительно начала отсчета. ![y=\sqrt[5]{2x+8} LaTeX formula: y=\sqrt[5]{2x+8}](/uploads/formulas/95bdff70178080e93c1c775e0d41223ebccb62ca.1.1.png) .
. явно:
явно:  ,
,  ,
,  .
.  на
на  , а
, а  на
на  , получим:
, получим: ![y=\sqrt[5]{2x+8} LaTeX formula: y=\sqrt[5]{2x+8}](/uploads/formulas/95bdff70178080e93c1c775e0d41223ebccb62ca.1.1.png) .
.![y=\sqrt[5]{2x+8} LaTeX formula: y=\sqrt[5]{2x+8}](https://helpy.quali.me/uploads/formulas/95bdff70178080e93c1c775e0d41223ebccb62ca.1.1.png) .
.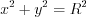 нельзя считать функцией, так как каждому значению
нельзя считать функцией, так как каждому значению  соответствует два значения
соответствует два значения  .
. 
