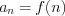, где 
. (5.1)
Подставляя в формулу 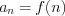вместо 
натуральные числа, получать последовательные члены данной последовательности
. (5.2)
Число 
называют первым членом последовательности,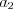 
– вторым, 
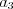– третьим, 
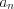– -ым ее членом и т. д., а число – номером члена последовательности.
Числовая последовательность может иметь как бесконечное число членов, так и конечное их число.
Н а п р и м е р:
1) множество четных натуральных чисел бесконечно: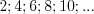 
;
2) множество четных натуральных двузначных чисел конечно: 
; 
; 
; ...; 
; 
.
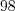Монотонные последовательности
Если для любого 
выполняется условие:
а)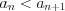 
, то последовательность возрастающая ;
б) если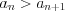 
, то последовательность убывающая ;
в) если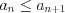 
, то последовательность не убывающая ;
г) если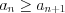 
, то последовательность не возрастающая .
Возрастающие, убывающие, невозрастающие и неубывающие последовательности называются монотонными .
Н а п р и м е р:
1) монотонная последовательность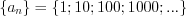 
возрастает;
2) монотонная последовательность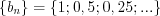 
убывает;
3) монотонная последовательность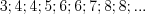 
не убывает.
Способы задания числовой последовательности
1. Способ задания последовательности с помощью формулы, называют аналитическим .
2. Если члены последовательности расположены в порядке возрастания их номера в таблице, то имеем табличный способ задания последовательности.
Н а п р и м е р:
3. Если задан первый член последовательности и указана формула, позволяющая по номеру и предыдущему члену 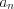найти следующий 
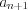ее член, то такой способ задания последовательности называют
рекуррентным .
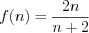. Решение. Подставляя в формулу вместо
натуральные числа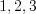 
и 
, получим:
; 
; 
; 
.
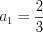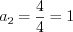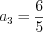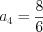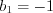, а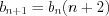 
. Решение.
.
. 
. 
.
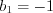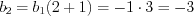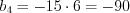