Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 , (4.27)
, (4.27)  . (4.28)
. (4.28) . (4.29)
. (4.29) . (4.30)
. (4.30) , (4.31)
, (4.31)
 ,
,  ,
,  .
. ,
, ,
, ,
,  ,
,  .
. ,
,  ,
,
1. Общее уравнение плоскости имеет вид:
 , (4.27)
, (4.27) где  – нормальный вектор этой плоскости.
– нормальный вектор этой плоскости.
 – нормальный вектор этой плоскости.
– нормальный вектор этой плоскости.Например,  – нормальный вектор плоскости
– нормальный вектор плоскости  .
.
 – нормальный вектор плоскости
– нормальный вектор плоскости  .
.2. Если известна точка 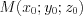 , принадлежащая плоскости, и нормальный вектор этой плоскости
, принадлежащая плоскости, и нормальный вектор этой плоскости  , то уравнение плоскости задают в виде:
, то уравнение плоскости задают в виде:
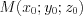 , принадлежащая плоскости, и нормальный вектор этой плоскости
, принадлежащая плоскости, и нормальный вектор этой плоскости  , то уравнение плоскости задают в виде:
, то уравнение плоскости задают в виде: . (4.28)
. (4.28)3. Если известны три точки 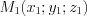 ,
, 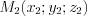 и
и  , принадлежащие плоскости, то уравнение этой плоскости можно найти по формуле:
, принадлежащие плоскости, то уравнение этой плоскости можно найти по формуле:
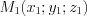 ,
, 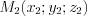 и
и  , принадлежащие плоскости, то уравнение этой плоскости можно найти по формуле:
, принадлежащие плоскости, то уравнение этой плоскости можно найти по формуле:  . (4.29)
. (4.29)4. Если известно, что вектор 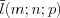 параллелен плоскости, проходящей через точки
параллелен плоскости, проходящей через точки 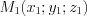 и
и 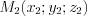 , то уравнение этой плоскости можно найти по формуле:
, то уравнение этой плоскости можно найти по формуле:
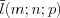 параллелен плоскости, проходящей через точки
параллелен плоскости, проходящей через точки 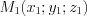 и
и 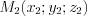 , то уравнение этой плоскости можно найти по формуле:
, то уравнение этой плоскости можно найти по формуле: . (4.30)
. (4.30)5. Уравнение плоскости в отрезках имеет вид:
 , (4.31)
, (4.31)где  ,
,  и
и  – алгебраические величины отрезков, которые отсекает плоскость на осях координат (
– алгебраические величины отрезков, которые отсекает плоскость на осях координат (  на оси
на оси  ,
,  на
на  и
и  на
на  ).
).
 ,
,  и
и  – алгебраические величины отрезков, которые отсекает плоскость на осях координат (
– алгебраические величины отрезков, которые отсекает плоскость на осях координат (  на оси
на оси  ,
,  на
на  и
и  на
на  ).
).Пример 1. Найдите уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
 параллельно плоскости
параллельно плоскости  .
.Решение. Так как искомая плоскость параллельна плоскости  , то нормальный вектор этой плоскости
, то нормальный вектор этой плоскости  является нормалью и искомой плоскости.
является нормалью и искомой плоскости.
 , то нормальный вектор этой плоскости
, то нормальный вектор этой плоскости  является нормалью и искомой плоскости.
является нормалью и искомой плоскости.Согласно формуле 4.28 запишем уравнение искомой плоскости:
 ,
,  ,
,  .
.Ответ:  .
.
 .
. Пример 2. Найдите уравнение плоскости, проходящей через точки  ,
,  и
и  .
.
 ,
,  и
и  .
.Решение. Согласно формуле 4.29 получим:
 ,
, ,
, ,
,  ,
, .
.Ответ:  .
.
 .
. Пример 3. Запишите уравнение плоскости, проходящей через точки  и
и  перпендикулярно плоскости
перпендикулярно плоскости  .
.
 и
и  перпендикулярно плоскости
перпендикулярно плоскости  .
.Решение. Так как искомая плоскость перпендикулярна плоскости  , то нормальный вектор этой плоскости
, то нормальный вектор этой плоскости  является направляющим вектором
является направляющим вектором  искомой плоскости.
искомой плоскости.
 , то нормальный вектор этой плоскости
, то нормальный вектор этой плоскости  является направляющим вектором
является направляющим вектором  искомой плоскости.
искомой плоскости. Согласно формуле 4.30 получим:
 ,
,  ,
,откуда  ,
,  ,
,  .
.
 ,
,  ,
,  .
.Ответ:  .
.
 .
. Если 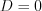 , то плоскость
, то плоскость  проходит через начало координат.
проходит через начало координат.
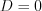 , то плоскость
, то плоскость  проходит через начало координат.
проходит через начало координат. Если  , то плоскость
, то плоскость  параллельна оси
параллельна оси 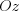 .
.
 , то плоскость
, то плоскость  параллельна оси
параллельна оси 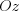 .
. Если  и
и 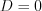 , то плоскость
, то плоскость  проходит через ось
проходит через ось 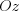 .
.
 и
и 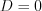 , то плоскость
, то плоскость  проходит через ось
проходит через ось 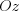 .
. Если  и
и  , то плоскость
, то плоскость  параллельна плоскости
параллельна плоскости  .
.
 и
и  , то плоскость
, то плоскость  параллельна плоскости
параллельна плоскости  .
. Если  ,
,  и
и 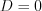 , то плоскость
, то плоскость  – координатная плоскость
– координатная плоскость  .
.
 ,
,  и
и 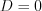 , то плоскость
, то плоскость  – координатная плоскость
– координатная плоскость  .
.
