Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 , (4.1)
, (4.1) . (4.2)
. (4.2)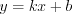 . (4.3)
. (4.3)  , где
, где  – угол наклона прямой к положительному направлению оси
– угол наклона прямой к положительному направлению оси  .
.  . (4.4)
. (4.4) , (4.5)
, (4.5) . (4.6)
. (4.6) , (4.7)
, (4.7)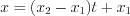 (4.8.1) ,
(4.8.1) , 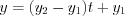 . (4.8.2)
. (4.8.2) . (4.9)
. (4.9) . (4.10)
. (4.10) . (4.11)
. (4.11) и
и  . (4.12)
. (4.12) и
и  . (4.13)
. (4.13) . (4. 14)
. (4. 14)
 ,
,  ,
,  ,
,  .
. ,
, .
. .
.
Уравнения прямой
1. Общее уравнение прямой на плоскости имеет вид:
 , (4.1)
, (4.1)где  , а
, а  – нормальный вектор этой прямой.
– нормальный вектор этой прямой.
 , а
, а  – нормальный вектор этой прямой.
– нормальный вектор этой прямой.Если известна точка  , принадлежащая прямой, и нормальный вектор прямой
, принадлежащая прямой, и нормальный вектор прямой  , то уравнение этой прямой можно найти по формуле:
, то уравнение этой прямой можно найти по формуле:
 , принадлежащая прямой, и нормальный вектор прямой
, принадлежащая прямой, и нормальный вектор прямой  , то уравнение этой прямой можно найти по формуле:
, то уравнение этой прямой можно найти по формуле:  . (4.2)
. (4.2)2. Уравнение прямой с угловым коэффициентом  имеет вид:
имеет вид:
 имеет вид:
имеет вид: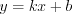 . (4.3)
. (4.3)Угловой коэффициент  прямой
прямой 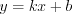 находят по формуле:
находят по формуле:
 прямой
прямой 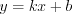 находят по формуле:
находят по формуле: , где
, где  – угол наклона прямой к положительному направлению оси
– угол наклона прямой к положительному направлению оси  .
. При этом:
1) если  , то функция монотонно возрастает;
, то функция монотонно возрастает;
 , то функция монотонно возрастает;
, то функция монотонно возрастает; 2) если  , то функция монотонно убывает;
, то функция монотонно убывает;
 , то функция монотонно убывает;
, то функция монотонно убывает;3) если  , то функция примет вид
, то функция примет вид 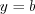 (семейство прямых, параллельных оси
(семейство прямых, параллельных оси  );
);
 , то функция примет вид
, то функция примет вид 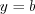 (семейство прямых, параллельных оси
(семейство прямых, параллельных оси  );
); 4) если  , то функция примет вид
, то функция примет вид  . Такую функциональную зависимость называют прямой пропорциональностью.
. Такую функциональную зависимость называют прямой пропорциональностью.
 , то функция примет вид
, то функция примет вид  . Такую функциональную зависимость называют прямой пропорциональностью.
. Такую функциональную зависимость называют прямой пропорциональностью. Если известна точка  , принадлежащая прямой, и угловой коэффициент
, принадлежащая прямой, и угловой коэффициент  прямой, то уравнение этой прямой можно найти по формуле:
прямой, то уравнение этой прямой можно найти по формуле:
 , принадлежащая прямой, и угловой коэффициент
, принадлежащая прямой, и угловой коэффициент  прямой, то уравнение этой прямой можно найти по формуле:
прямой, то уравнение этой прямой можно найти по формуле:  . (4.4)
. (4.4)3. Каноническое уравнение прямой имеет вид:
 , (4.5)
, (4.5)где  – точка, принадлежащая этой прямой, а
– точка, принадлежащая этой прямой, а  – направляющий вектор прямой.
– направляющий вектор прямой.
 – точка, принадлежащая этой прямой, а
– точка, принадлежащая этой прямой, а  – направляющий вектор прямой.
– направляющий вектор прямой. Если известны координаты точек  и
и  , принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
, принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
 и
и  , принадлежащих прямой, то уравнение этой прямой можно найти по формуле:
, принадлежащих прямой, то уравнение этой прямой можно найти по формуле:  . (4.6)
. (4.6)4. Уравнение прямой в отрезках имеет вид:
 , (4.7)
, (4.7)где  и
и  – алгебраические величины отрезков, которые отсекает прямая на осях координат (
– алгебраические величины отрезков, которые отсекает прямая на осях координат (  на оси
на оси  и
и  на оси
на оси  ).
).
 и
и  – алгебраические величины отрезков, которые отсекает прямая на осях координат (
– алгебраические величины отрезков, которые отсекает прямая на осях координат (  на оси
на оси  и
и  на оси
на оси  ).
).Например, если  , а
, а  , то
, то  .
.
 , а
, а  , то
, то  .
.5. Чтобы записать параметрические уравнения прямой, можно воспользоваться равенством 4.5 или 4.6. Например, полагая , получим:
, получим:
 , получим:
, получим: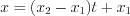 (4.8.1) ,
(4.8.1) , 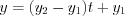 . (4.8.2)
. (4.8.2)Взаимное расположение прямых
Рассмотрим прямые  и
и  .
.
 и
и  .
.1. Прямые пересекаются, если
 . (4.9)
. (4.9)Например, прямые  и
и  пересекаются, так как
пересекаются, так как  , а
, а  и
и  .
.
 и
и  пересекаются, так как
пересекаются, так как  , а
, а  и
и  .
. Угол между прямыми находят по формуле:
 . (4.10)
. (4.10)2. Прямые перпендикулярны, если выполняется условие:
 . (4.11)
. (4.11)Например, прямые  и
и  перпендикулярны, так как
перпендикулярны, так как  , а
, а  и
и  .
.
 и
и  перпендикулярны, так как
перпендикулярны, так как  , а
, а  и
и  .
. 3. Прямые параллельны, если
 и
и  . (4.12)
. (4.12)Например, прямые  и
и  параллельны, так как
параллельны, так как  и
и  .
.
 и
и  параллельны, так как
параллельны, так как  и
и  .
. 4. Прямые совпадают, если:
 и
и  . (4.13)
. (4.13)Например, прямые  и
и  совпадают.
совпадают.
 и
и  совпадают.
совпадают.Расстояние от точки  до прямой
до прямой  находят по формуле:
находят по формуле:
 до прямой
до прямой  находят по формуле:
находят по формуле: . (4. 14)
. (4. 14) Пример 1. Запишите в общем виде уравнение прямой, если известно, что ей принадлежат точки  и
и  .
.
 и
и  .
.Решение. Уравнение данной прямой найдем по формуле 4.6:
 ,
,  ,
,  ,
,  .
.Ответ:  .
.
 .
.Пример 2. Запишите уравнение прямой, если известно, что эта прямая проходит через точку  и параллельна прямой
и параллельна прямой  .
.
 и параллельна прямой
и параллельна прямой  .
.Решение. Запишем уравнение данной прямой в виде 4.3:
 ,
, .
.Ответ:  .
.
 .
.Пример 3. Запишите параметрические уравнения прямой, которая проходит через точку  перпендикулярно прямой
перпендикулярно прямой  .
.
 перпендикулярно прямой
перпендикулярно прямой  .
. Решение. 1. Так как искомая прямая перпендикулярна прямой  , то нормальный вектор прямой 4.1 имеет вид:
, то нормальный вектор прямой 4.1 имеет вид:  . Этот вектор будет направляющим вектором искомой прямой:
. Этот вектор будет направляющим вектором искомой прямой:  .
.
 , то нормальный вектор прямой 4.1 имеет вид:
, то нормальный вектор прямой 4.1 имеет вид:  . Этот вектор будет направляющим вектором искомой прямой:
. Этот вектор будет направляющим вектором искомой прямой:  .
. 2. Согласно формуле 4.5 запишем уравнение искомой прямой:
 .
.Полагая  , получим
, получим  и
и  .
.
 , получим
, получим  и
и  .
. Ответ:  , а
, а  .
.
 , а
, а  .
. Координаты направляющего вектора прямой 4.5 определяются с точностью до постоянного множителя 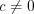 :
:  .
.
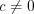 :
:  .
. Например,  и
и  , а также
, а также  – направляющие векторы прямой
– направляющие векторы прямой  .
.
 и
и  , а также
, а также  – направляющие векторы прямой
– направляющие векторы прямой  .
. 




 .
.
