Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
(3.3) 
; (3.3.1)
; (3.3.2)
. (3.3.3)
(3.4)
(3.5) 
(3.6) 
(3.7)
и 
. 
откуда 
и 
Следовательно, 
.png "x=\frac{5+\frac{2}{3}\cdot (-1)}{1+\frac{2}{3}}")
; .png "x=\frac{-2+\frac{2}{3}\cdot 4}{1+\frac{2}{3}}=\frac{-6+8}{3+2}=\frac{2}{5}")
; .png "z=\frac{0+\frac{2}{3}\cdot 3}{1+\frac{2}{3}}=\frac{6}{3+2}=\frac{6}{5}")
.
; 
; 
.
Вектором называют направленный отрезок.
Начало и конец вектора обозначают двумя прописными буквами латинского алфавита или одной строчной буквой и записывают:
или 
Начало и конец вектора обозначают двумя прописными буквами латинского алфавита или одной строчной буквой и записывают:
или На рисунке 3.1 изображен вектор 
, у которого точка 
– начало, а точка 
– его конец, и вектор 
, у которого точка 
– его начало, а точка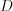 
– его конец.
, у которого точка – начало, а точка – его конец, и вектор , у которого точка – его начало, а точка 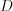– его конец.Нуль-вектором называют вектор, начало и конец которого совпадают.
Нуль-вектор изображают точкой и записывают
(рис. 3.1).
Нуль-вектор изображают точкой и записывают
(рис. 3.1).Единичным вектором называют вектор, длина которого равна единице.
Упорядоченную совокупность 
действительных чисел 
называют точкой, а сами эти числа – ее координатами. Записывают: 
Множество таких всевозможных точек называют координатным n-мерным пространством и обозначают 
действительных чисел называют точкой, а сами эти числа – ее координатами. Записывают: Множество таких всевозможных точек называют координатным n-мерным пространством и обозначают Разложение вектора по ортам
1. Рассмотрим двумерное пространство с заданной в нем системой координат (рис. 3.2). На оси 
отложим единичный вектор 
, начало которого совпадает с началом отсчета, а направление – с положительным направлением оси . Аналогичным образом отложим на оси 
вектор 
.
Векторы и 
называют координатными векторами (ортами) прямоугольной системы координат.
отложим единичный вектор , начало которого совпадает с началом отсчета, а направление – с положительным направлением оси . Аналогичным образом отложим на оси вектор . Векторы
и называют координатными векторами (ортами) прямоугольной системы координат. Любой вектор 
на плоскости можно разложить по ортам: 
на плоскости можно разложить по ортам: Говорят, что 
и 
–координаты вектора и записывают: 
и –координаты вектора и записывают: Вектор, начало которого совпадает с началом отсчета, называют радиус-вектором. На рисунке 3.2 изображен радиус-вектор 
2. Рассмотрим трехмерное пространство с заданной в нем декартовой системой координат (рис. 3.3). Единичные векторы 
и 
–координатные векторы (орты) прямоугольной системы координат. Любой вектор 
пространства можно разложить по ортам:
и –координатные векторы (орты) прямоугольной системы координат. Любой вектор пространства можно разложить по ортам: Говорят, что 
и 
–координаты вектора 
и записывают: 
и –координаты вектора и записывают: Координаты вектора
1. Чтобы найти координаты вектора, необходимо из координат конца вектора вычесть соответствующие координаты его начала. Если вектор задан в двумерном пространстве, и точка 
– его начало, а точка 
– его конец, то он имеет две координаты 
и 
, которые записывают в круглых скобках вслед за названием вектора или без названия вектора: 
или 
задан в двумерном пространстве, и точка – его начало, а точка – его конец, то он имеет две координаты и , которые записывают в круглых скобках вслед за названием вектора или без названия вектора: или Если вектор задан в трехмерном пространстве и точка 
– его начало, а точка 
– его конец, то записывают: 
– его начало, а точка – его конец, то записывают: 2. Координаты середины вектора (середины вектора): если точки 
и 
– концы отрезка, а точка 
– его середина, то точка будет иметь координаты:
и – концы отрезка, а точка – его середина, то точка будет иметь координаты: (3.3) 3. Деление отрезка в заданном отношении: если точки 
и – концы отрезка 
, а точка 
делит этот отрезок в отношении 
(считая от точки ), то координаты точки находят по формулам:
и – концы отрезка , а точка делит этот отрезок в отношении (считая от точки ), то координаты точки находят по формулам: ; (3.3.1); (3.3.2). (3.3.3)Длина вектора
Длину вектора записывают и читают: модуль вектора или длина вектора .
и читают: модуль вектора или длина вектора . 1. Если известны координаты точек 
– начала и 
– конца вектора, то длину вектора (длину отрезка) находят по формуле:
– начала и – конца вектора, то длину вектора (длину отрезка) находят по формуле: (3.4)2. Если известны координаты вектора 
, то длину вектора находят по формуле:
, то длину вектора находят по формуле: (3.5)Взаимное расположение векторов
1. Коллинеарными называют векторы, лежащие на параллельных прямых (или на одной прямой).
На рисунке 3.4 изображены коллинеарные векторы 
и 
и Условие коллинеарности векторов: векторы 
и 
коллинеарны, если их соответствующие координаты пропорциональны, то есть если выполняется равенство
и коллинеарны, если их соответствующие координаты пропорциональны, то есть если выполняется равенство (3.6)При этом, если:
а) 
, то векторы сонаправлены;
, то векторы сонаправлены; б) 
, то векторы противоположно направлены.
, то векторы противоположно направлены. Например: 1) На рисунке 3.4 векторы 
и 
, а также 
и 
сонаправлены. Записывают: 
и 
и , а также и сонаправлены. Записывают: и 2) На рисунке 3.4 вектор и , а также векторы и противоположно направлены. Записывают: 
и 
и , а также векторы и противоположно направлены. Записывают: и 2. Противоположными называют векторы, имеющие равные длины и противоположно направленные.
Вектор, противоположный вектору , записывают: 
или 
.
, записывают: или . Вектор, противоположный вектору , записывают: 
(рис. 3.5).
, записывают: (рис. 3.5).3. Компланарными называют векторы, лежащие в параллельных плоскостях или в одной плоскости.
На рисунке 3.6 изображен прямой параллелепипед. Векторы , и , а также векторы , и компланарны. Векторы , и 
, а также векторы , и 
не компланарны.
, и , а также векторы , и компланарны. Векторы , и , а также векторы , и не компланарны.Условие компланарности трех векторов: векторы , 
и 
компланарны, если определитель, составленный из координат этих векторов, равен нулю:
, и компланарны, если определитель, составленный из координат этих векторов, равен нулю: (3.7)Пример 1. Найдите координаты вектора 
, если известны точки 
и 
.
, если известны точки и .Решение. Вычитая из координат конца вектора соответствующие координаты его начала, получим:
Ответ: 
Пример 2. Известны координаты точки 
, которая является серединой отрезка , и координаты точки 
. Найдите координаты точки 
, которая является серединой отрезка , и координаты точки . Найдите координаты точки Решение. Согласно формуле 3.3 запишем:
и . Решая уравнения, получим: 
и 
.
и .Ответ: 
Пример 3. Найдите модуль разности длин векторов 
и 
и Решение. Согласно формуле 3.5 получим:
Тогда 
Ответ: 
Пример 4. Векторы 
и 
коллинеарны. Найдите сумму чисел 
и 
и коллинеарны. Найдите сумму чисел и Решение. Согласно формуле 3.6
откуда и Следовательно, Ответ: 
Пример 5. Найдите значение 
если известно, что векторы 
и 
компланарны.
если известно, что векторы и компланарны.Решение. Согласно формуле 3.7 составим и решим уравнение:
Ответ: 
Пример 6. Найдите координаты точки , если известны координаты концов отрезка .png "A(5;-2;0)")
и .png "B(-1;4;3)")
, а точка делит отрезок в отношении 2 : 3, считая от точки .
, если известны координаты концов отрезка и , а точка делит отрезок в отношении 2 : 3, считая от точки ..png "l=\frac{2}{3}")
, ; ; .Ответ: .png "M(2,6;0,4;1,2)")
1. Аналогично находят координаты и длину n-мерного вектора 
2. Различайте модуль числа и модуль вектора. Например:
1) найдем модули чисел 
и 
и 2) найдем модуль вектора 
по формуле 3.5 :
по формуле 3.5 :3. Если точки и — концы отрезка , а точка 
делит этот отрезок в отношении .png "l=\frac{BM}{MA}")
(считая от точки ), то координаты точки 
находят по формулам:
и — концы отрезка , а точка делит этот отрезок в отношении (считая от точки ), то координаты точки находят по формулам: ; ; .Длина вектора
Координаты вектора
Деление отрезка в заданном отношении