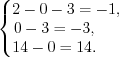Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
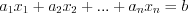 , (2.1)
, (2.1)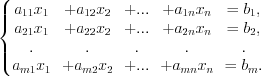 (2.2)
(2.2)![X=\left [ x_{1}\; \; \; \; \; x_{2}\; \; \; \; \; ...\; \; \; \; \; x_{n} \right ]^{T} LaTeX formula: X=\left [ x_{1}\; \; \; \; \; x_{2}\; \; \; \; \; ...\; \; \; \; \; x_{n} \right ]^{T}](/uploads/formulas/af0c8c39739886e04cffdd8579a87ec7a1d0d86d.1.1.png) ; (2.3)
; (2.3) ; (2.4)
; (2.4)![B=\left [ b_{1}\; \; \; \; \; b_{2}\; \; \; \; \;\cdots \; \; \; \; \; b_{n} \right ]^{^{T}} LaTeX formula: B=\left [ b_{1}\; \; \; \; \; b_{2}\; \; \; \; \;\cdots \; \; \; \; \; b_{n} \right ]^{^{T}}](/uploads/formulas/24fb38f1cbbd29e1d0479a5b9916182ce09d968b.1.1.png) ; (2.5)
; (2.5)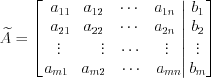 . (2.6)
. (2.6)
Линейным уравнением с  переменными называют уравнение вида
переменными называют уравнение вида
 переменными называют уравнение вида
переменными называют уравнение вида 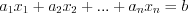 , (2.1)
, (2.1)где 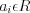 ,
, 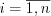 ,
, 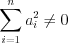 ;
;  .
.
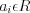 ,
, 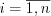 ,
, 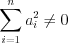 ;
;  .
. Числа 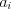 называют коэффициентами при переменных, а число
называют коэффициентами при переменных, а число  – свободным членом.
– свободным членом.
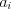 называют коэффициентами при переменных, а число
называют коэффициентами при переменных, а число  – свободным членом.
– свободным членом.Запись 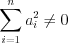 означает, что все коэффициенты при переменных одновременно не могут быть равны нулю.
означает, что все коэффициенты при переменных одновременно не могут быть равны нулю.
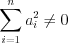 означает, что все коэффициенты при переменных одновременно не могут быть равны нулю.
означает, что все коэффициенты при переменных одновременно не могут быть равны нулю. Системой линейных уравнений называют множество линейных уравнений с  неизвестными (
неизвестными (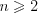 ), для которых требуется найти значения неизвестных, удовлетворяющих всем уравнениям системы.
), для которых требуется найти значения неизвестных, удовлетворяющих всем уравнениям системы.
 неизвестными (
неизвестными (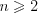 ), для которых требуется найти значения неизвестных, удовлетворяющих всем уравнениям системы.
), для которых требуется найти значения неизвестных, удовлетворяющих всем уравнениям системы.Система, состоящая из  уравнений и содержащая
уравнений и содержащая  переменных уравнений, имеет вид:
переменных уравнений, имеет вид:
 уравнений и содержащая
уравнений и содержащая  переменных уравнений, имеет вид:
переменных уравнений, имеет вид: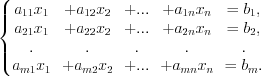 (2.2)
(2.2)Числа 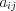 называют коэффициентами при переменных, а числа
называют коэффициентами при переменных, а числа 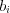 – свободными членами
– свободными членами  .
.
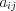 называют коэффициентами при переменных, а числа
называют коэффициентами при переменных, а числа 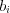 – свободными членами
– свободными членами  .
.Если все свободные члены равны нулю, то такая система уравнений называется однородной.
Матрицы системы (2.2):
1) искомая матрица Х системы состоит из переменных:
![X=\left [ x_{1}\; \; \; \; \; x_{2}\; \; \; \; \; ...\; \; \; \; \; x_{n} \right ]^{T} LaTeX formula: X=\left [ x_{1}\; \; \; \; \; x_{2}\; \; \; \; \; ...\; \; \; \; \; x_{n} \right ]^{T}](/uploads/formulas/af0c8c39739886e04cffdd8579a87ec7a1d0d86d.1.1.png) ; (2.3)
; (2.3)2) основная матрица системы А состоит из коэффициентов при переменных:
 ; (2.4)
; (2.4)3) матрица-столбец В состоит из свободных членов системы:
![B=\left [ b_{1}\; \; \; \; \; b_{2}\; \; \; \; \;\cdots \; \; \; \; \; b_{n} \right ]^{^{T}} LaTeX formula: B=\left [ b_{1}\; \; \; \; \; b_{2}\; \; \; \; \;\cdots \; \; \; \; \; b_{n} \right ]^{^{T}}](/uploads/formulas/24fb38f1cbbd29e1d0479a5b9916182ce09d968b.1.1.png) ; (2.5)
; (2.5)4) расширенная матрица системы состоит из коэффициентов при переменных и свободных членов:
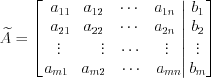 . (2.6)
. (2.6)Решением системы является упорядоченная совокупность чисел, при подстановке которых в систему каждое из ее уравнений обращается в верное равенство.
Решить систему уравнений – значит найти все ее решения или показать, что эта система решений не имеет.
Система, которая имеет хотя бы одно решение, называется совместной. Если система имеет только одно решение, то она называется определенной, а если имеет бесконечно много решений – неопределенной.
Система, которая не имеет ни одного решения, называется несовместной.
Однородная система линейных уравнений всегда совместна.
Матрицы СЛАУ


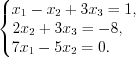
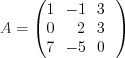 ;
;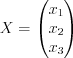 ;
;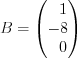 ;
;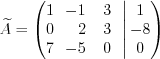 .
.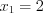 ,
, 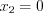 и
и 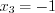 образуют решение системы уравнений
образуют решение системы уравнений