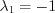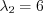Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (1.19)
. (1.19)
 ,
, 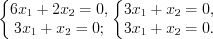
 ,
, 
Число  называют собственным значением (собственным числом) матрицы
называют собственным значением (собственным числом) матрицы 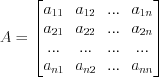 , если существует ненулевой вектор
, если существует ненулевой вектор  , для которого выполняется равенство
, для которого выполняется равенство  . (1.18)
. (1.18)
 называют собственным значением (собственным числом) матрицы
называют собственным значением (собственным числом) матрицы 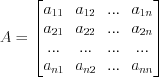 , если существует ненулевой вектор
, если существует ненулевой вектор  , для которого выполняется равенство
, для которого выполняется равенство  . (1.18)
. (1.18)Вектор  называют собственным вектором матрицы
называют собственным вектором матрицы  , соответствующим данному собственному значению
, соответствующим данному собственному значению  .
.
 называют собственным вектором матрицы
называют собственным вектором матрицы  , соответствующим данному собственному значению
, соответствующим данному собственному значению  .
.Собственные числа  ,
,  ,
,  , … ,
, … ,  матрицы (1.2) находят, решая уравнение
матрицы (1.2) находят, решая уравнение  или
или
 ,
,  ,
,  , … ,
, … ,  матрицы (1.2) находят, решая уравнение
матрицы (1.2) находят, решая уравнение  или
или . (1.19)
. (1.19)Собственный вектор  , соответствующий собственному значению
, соответствующий собственному значению  , находят, решая однородную систему линейных алгебраических уравнений
, находят, решая однородную систему линейных алгебраических уравнений
 . (1.20)
. (1.20)
 , соответствующий собственному значению
, соответствующий собственному значению  , находят, решая однородную систему линейных алгебраических уравнений
, находят, решая однородную систему линейных алгебраических уравнений . (1.20)
. (1.20)Пример 1. Найдите собственные значения и собственные векторы матрицы  .
.
 .
.Найдем собственный вектор  , соответствующий собственному числу
, соответствующий собственному числу  .
.
Для этого согласно формуле 1.20 составим и решим систему уравнений:
 , соответствующий собственному числу
, соответствующий собственному числу  .
. Для этого согласно формуле 1.20 составим и решим систему уравнений:
 ,
, 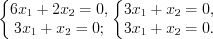
Пусть  (
( – любое отличное от нуля действительное число), тогда
– любое отличное от нуля действительное число), тогда  .
.
Полагая, например, , запишем:
, запишем: .
.
 (
( – любое отличное от нуля действительное число), тогда
– любое отличное от нуля действительное число), тогда  .
. Полагая, например,
 , запишем:
, запишем: .
.Аналогично найдем собственный вектор  , соответствующий собственному числу
, соответствующий собственному числу  :
:
 , соответствующий собственному числу
, соответствующий собственному числу  :
:  ,
, 
Пусть  , тогда
, тогда  . Полагая, например,
. Полагая, например,  , запишем:
, запишем: 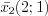 .
.
 , тогда
, тогда  . Полагая, например,
. Полагая, например,  , запишем:
, запишем: 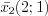 .
.Ответ: 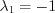 ,
, 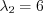 ,
,  ,
, 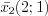 .
.
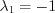 ,
, 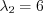 ,
,  ,
, 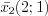 .
.Каждому собственному числу матрицы может соответствовать множество коллинеарных собственных векторов.