Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ; (1.11)
; (1.11)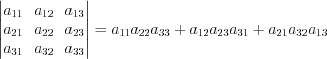
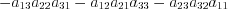 ; (1.12)
; (1.12)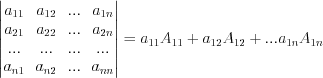 , (1.13)
, (1.13)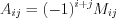 . (1.14)
. (1.14)
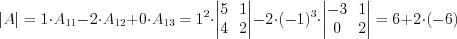
 .
.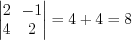 .
. 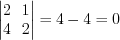 .
.
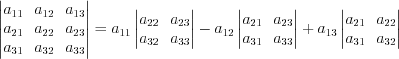 .
. 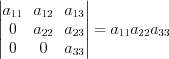 .
.
Определитель матрицы
Для определителя матрицы употребляются обозначения: 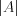 ,
, 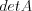 ,
, 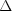 .
.
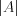 ,
, 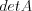 ,
, 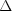 .
.Определитель квадратной матрицы – это число, которое находят по формулам:
 ; (1.11)
; (1.11)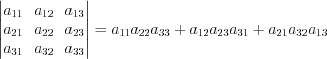
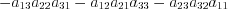 ; (1.12)
; (1.12)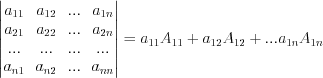 , (1.13)
, (1.13)где 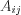 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 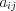 матрицы
матрицы  .
.
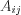 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 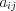 матрицы
матрицы  .
.Замечание. В формуле 1.13 определитель разложен по элементам первой строки. Тот же результат получим, если разложим определитель по элементам любой строки или любого столбца.
Минор
Минор 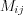 элемента
элемента 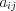 квадратной матрицы – это определитель этой матрицы, у которого отсутствует
квадратной матрицы – это определитель этой матрицы, у которого отсутствует  -я строка и
-я строка и 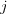 -й столбец.
-й столбец.
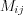 элемента
элемента 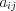 квадратной матрицы – это определитель этой матрицы, у которого отсутствует
квадратной матрицы – это определитель этой матрицы, у которого отсутствует  -я строка и
-я строка и 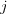 -й столбец.
-й столбец. Алгебраическое дополнение
Алгебраическое дополнение 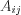 элемента
элемента 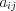 квадратной матрицы находят по формуле:
квадратной матрицы находят по формуле:
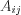 элемента
элемента 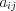 квадратной матрицы находят по формуле:
квадратной матрицы находят по формуле: 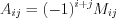 . (1.14)
. (1.14)Свойства определителей
1. Определитель не изменится при замене всех его строк соответствующими столбцами.
Например, 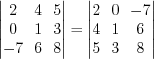 .
.
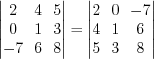 .
.2. При перестановке двух соседних строк (столбцов) определитель меняет знак.
Например,  .
.
 .
.3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Например,  .
.
 .
.4. Общий множитель строки (столбца) можно выносить за знак определителя.
Например, 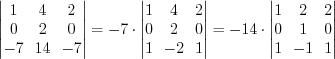 .
.
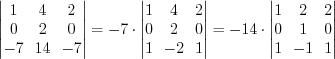 .
.5. Если все элементы некоторой строки (столбца) равны нулю, то определитель равен нулю.
Например,  .
.
 .
.6. Если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умножив их на одно и то же отличное от нуля число, то определитель не изменится.
Например, 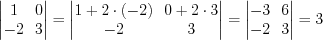 .
.
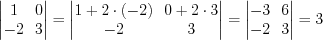 .
.Ранг матрицы
Если в матрице произвольным образом выбрать строк и
строк и столбцов и из элементов, стоящих на пересечении этих строк и столбцов, составить определитель, то получим минор порядка
столбцов и из элементов, стоящих на пересечении этих строк и столбцов, составить определитель, то получим минор порядка этой матрицы.
этой матрицы.
 строк и
строк и столбцов и из элементов, стоящих на пересечении этих строк и столбцов, составить определитель, то получим минор порядка
столбцов и из элементов, стоящих на пересечении этих строк и столбцов, составить определитель, то получим минор порядка этой матрицы.
этой матрицы. Рангом матрицы называют наибольший из порядков отличных от нуля ее миноров.
Ранг матрицы  обозначают:
обозначают:  , или
, или 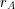 , или
, или 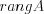 .
.
 обозначают:
обозначают:  , или
, или 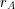 , или
, или 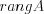 .
.Свойства ранга матрицы:
1. Ранги матрицы  и матрицы
и матрицы  равны.
равны.
 и матрицы
и матрицы  равны.
равны.2. Ранг матрицы не изменится, если из нее вычеркнуть или приписать к ней нулевую строку или нулевой столбец.
3. Ранг матрицы не изменится, если выполнить элементарные преобразования матрицы.
Пример 1. Найдем определитель матрицы 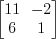 .
.
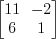 .
. Пример 2. Найдем определитель матрицы 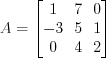 .
.
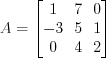 .
. Применяя формулу 1.12, получим:
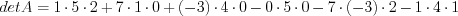
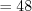 .
.
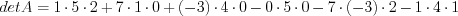
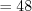 .
.Пример 3. Найдем миноры 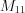 и
и 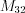 матрицы
матрицы 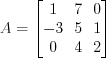 .
.
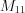 и
и 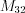 матрицы
матрицы 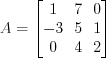 .
. Согласно определению минора получим:
1) 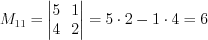 ;
;
2)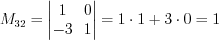 .
.
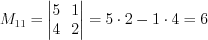 ;
; 2)
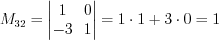 .
.Пример 4. Найдем алгебраические дополнения  и
и 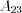 матрицы
матрицы 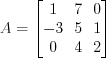 .
.
 и
и 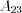 матрицы
матрицы 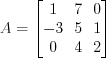 .
. Согласно формуле 1.14 получим:
1) 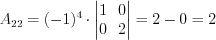 ;
;
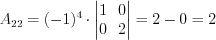 ;
; 2) 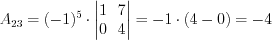 .
.
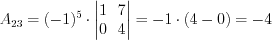 .
.Разложим определитель по элементам первой строки:
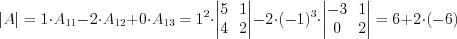
 .
.Пример 6. Найдем ранги матриц 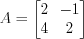 и
и 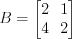 .
.
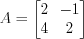 и
и 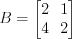 .
. 1. Вычислим минор второго порядка матрицы  :
:
 :
: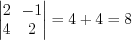 .
. Поскольку минор второго порядка не равен нулю, то ранг матрицы равен двум.
2. Вычислим минор второго порядка матрицы  :
:
 :
: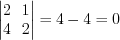 .
. Поскольку минор второго порядка равен нулю, то ранг матрицы меньше двух.
Так как все миноры первого порядка (элементы матрицы) отличны от нуля, то ранг матрицы равен .
.
Так как все миноры первого порядка (элементы матрицы) отличны от нуля, то ранг матрицы равен
 .
.1. Определитель матрицы третьего порядка можно вычислить по формуле:
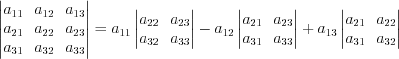 .
. 2. Определитель треугольной матрицы равен произведению ее диагональных элементов:
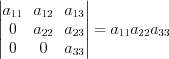 .
.3. Матрица, определитель которой равен нулю, называется вырожденной.
Определитель матрицы второго порядка
Определитель матрицы третьего порядка
Ранг матрицы
Минор матрицы
Минор элемента матрицы


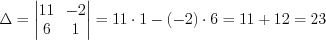
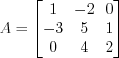 , применяя формулу
, применяя формулу