 является пределом числовой последовательности
является пределом числовой последовательности 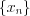 , если для любого сколь угодно малого
, если для любого сколь угодно малого 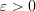 найдется такой номер
найдется такой номер  , что при всех
, что при всех  выполняется неравенство
выполняется неравенство  .
. 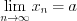 .
.Геометрический смысл предела: число  является пределом последовательности , если в любой его
является пределом последовательности , если в любой его  -окрестности содержатся почти все члены последовательности, а вне этой окрестности находится лишь конечное число ее членов (рис. 5.4).
-окрестности содержатся почти все члены последовательности, а вне этой окрестности находится лишь конечное число ее членов (рис. 5.4).
Сходимость последовательностей
Сходящейся называется числовая последовательность, предел которой существует.
Расходящейся называется числовая последовательность, предел которой равен бесконечности или не существует.
Н а п р и м е р:
1) числовая последовательность 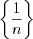 сходится и
сходится и 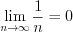 ;
;
2) числовая последовательность  расходится, так как при
расходится, так как при ее предел не существует.
Ограниченность последовательностей
Числовая последовательность 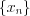 ограничена, если
ограничена, если  , то
, то  такое, что
такое, что 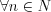 выполняется
выполняется  .
.
Числовая последовательность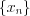 не ограничена, если
не ограничена, если 
 такое, что
такое, что 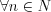 выполняется
выполняется  .
.
Н а п р и м е р: числовая последовательность  ограничена снизу.
ограничена снизу.
Если последовательность имеет предел, то она ограничена.
Бесконечно малые и большие последовательности
Числовая последовательность 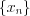 бесконечно малая, если
бесконечно малая, если 
 такой, что
такой, что 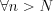 выполняется
выполняется  .
.
Числовая последовательность 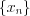 бесконечно большая, если
бесконечно большая, если 
 такой, что
такой, что  выполняется
выполняется  .
.
Н а п р и м е р, последовательность бесконечно малая, а последовательность
бесконечно малая, а последовательность  бесконечно большая при
бесконечно большая при  .
.
Квантор – общее название для логических операций, ограничивающих область истинности какого-либо утверждения, высказывания (предиката).
Квантор всеобщности обозначается 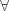 и читается: «для всех …» или «для любого …».
и читается: «для всех …» или «для любого …».
Квантор существования обозначается  и читается: «существует …» или «найдется …».
и читается: «существует …» или «найдется …».
Тогда определение числовой последовательности можем записать так:
число  является пределом числовой последовательности
является пределом числовой последовательности 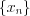 , если
, если 
 такой, что
такой, что  .
.

