Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

 . (10.32)
. (10.32)
 , (10.33)
, (10.33) . (10.33.1)
. (10.33.1) , (10.34)
, (10.34) . (10.34.1)
. (10.34.1) . (10.35)
. (10.35) . (10.36)
. (10.36) . (10.37)
. (10.37) . (10.38)
. (10.38) . (10.39)
. (10.39)

 ;
;
 .
.
Упорядоченная пара 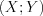 случайных величин
случайных величин  и
и  называется двумерной случайной величиной (или системой случайных величин).
называется двумерной случайной величиной (или системой случайных величин).
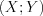 случайных величин
случайных величин  и
и  называется двумерной случайной величиной (или системой случайных величин).
называется двумерной случайной величиной (или системой случайных величин).Закон распределения двумерной случайной величины 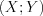 задан, если каждой паре значений
задан, если каждой паре значений  и
и  поставлена в соответствие вероятность и сумма всех вероятностей равна
поставлена в соответствие вероятность и сумма всех вероятностей равна  .
.
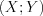 задан, если каждой паре значений
задан, если каждой паре значений  и
и  поставлена в соответствие вероятность и сумма всех вероятностей равна
поставлена в соответствие вероятность и сумма всех вероятностей равна  .
. Если случайная величина дискретная, то закон ее распределения может быть записан таблично:
Функция распределения
Функцией распределения двумерной случайной величины 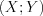 называют функцию вида
называют функцию вида
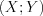 называют функцию вида
называют функцию вида . (10.32)
. (10.32)Геометрически это означает, что мы находим вероятность того, что случайная точка 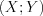 попадет в бесконечный квадрат с вершиной в точке
попадет в бесконечный квадрат с вершиной в точке 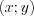 , так что точка
, так что точка 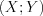 будет расположена ниже и левее точки
будет расположена ниже и левее точки 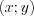 (рис. 10.4).
(рис. 10.4).
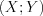 попадет в бесконечный квадрат с вершиной в точке
попадет в бесконечный квадрат с вершиной в точке 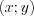 , так что точка
, так что точка 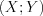 будет расположена ниже и левее точки
будет расположена ниже и левее точки 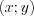 (рис. 10.4).
(рис. 10.4).
Числовые характеристики
1. Математические ожидания дискретных случайных величин, входящих в систему, находят по формулам:
 , (10.33)
, (10.33) . (10.33.1)
. (10.33.1)2. Дисперсии дискретных случайных величин, входящих в систему, находят по формулам:
 , (10.34)
, (10.34) . (10.34.1)
. (10.34.1)Ковариация
Ковариацией двух случайных величин  и
и  называют математическое ожидание произведения их отклонений от своих математических ожиданий:
называют математическое ожидание произведения их отклонений от своих математических ожиданий:
 и
и  называют математическое ожидание произведения их отклонений от своих математических ожиданий:
называют математическое ожидание произведения их отклонений от своих математических ожиданий:  . (10.35)
. (10.35)1. Ковариацию  и
и  можно найти по формуле:
можно найти по формуле:
 и
и  можно найти по формуле:
можно найти по формуле: . (10.36)
. (10.36)2. Случайные величины  и
и  независимые, если
независимые, если
 и
и  независимые, если
независимые, если  . (10.37)
. (10.37)3. Случайные величины X и Y зависимые, если
 . (10.38)
. (10.38)Корреляция
Коэффициентом корреляции двух случайных величин  и
и  называют число, которое характеризует степень зависимости
называют число, которое характеризует степень зависимости  и
и  и находят по формуле:
и находят по формуле:
 и
и  называют число, которое характеризует степень зависимости
называют число, которое характеризует степень зависимости  и
и  и находят по формуле:
и находят по формуле: . (10.39)
. (10.39)Свойства коэффициента корреляции
1.  .
.
 .
.2. В случае нормального распределения, если случайные величины  и
и  независимые, то
независимые, то  .
.
 и
и  независимые, то
независимые, то  .
.3. В случае нормального распределения, если случайные величины  и
и  связаны линейной зависимостью
связаны линейной зависимостью  , то
, то  или
или  .
.
 и
и  связаны линейной зависимостью
связаны линейной зависимостью  , то
, то  или
или  .
.Пример. Распределение системы случайных величин  и
и  представлено в таблице:
представлено в таблице:
 и
и  представлено в таблице:
представлено в таблице:
Найдите ковариацию.
 ;
;  .
. 2. Найдем  , перемножая соответствующие значения
, перемножая соответствующие значения  ,
,  ,
,  и складывая полученные произведения:
и складывая полученные произведения:

 .
.
 , перемножая соответствующие значения
, перемножая соответствующие значения  ,
,  ,
,  и складывая полученные произведения:
и складывая полученные произведения:
 .
.Ответ:  .
.
 .
.

