Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 , (10.17)
, (10.17)
 . (10.19)
. (10.19) . (10.20)
. (10.20) , (10.27)
, (10.27) . (10.31)
. (10.31)
 .
.

 .
.
Случайная величина – это величина, значения которой зависят от случая.
Случайная величина обозначается буквами  ,
,  ,
, 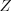 и т. д.
и т. д.
 ,
,  ,
, 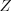 и т. д.
и т. д. Непрерывная  принимает все значения из заданного промежутка.
принимает все значения из заданного промежутка.
 принимает все значения из заданного промежутка.
принимает все значения из заданного промежутка.Функция распределения
Теоретическая функция распределения случайной величины  задается формулой:
задается формулой:
 задается формулой:
задается формулой:  , (10.17)
, (10.17)где  – вероятность того, что
– вероятность того, что  принимает значение, меньшее
принимает значение, меньшее  .
.
 – вероятность того, что
– вероятность того, что  принимает значение, меньшее
принимает значение, меньшее  .
. Свойства функции распределения
1.  .
.
 .
.2. Функция распределения неубывающая.
3. Функция распределения непрерывна слева.
4.  ,
,  .
.
 ,
,  .
.Н а п р и м е р, на рисунках 10.1 и 10.2 изображены графики функций распределения некоторых непрерывных случайных величин.

Плотность распределения
Плотностью распределения непрерывной случайной величины  в точке
в точке  называют функцию
называют функцию
 в точке
в точке  называют функцию
называют функцию  . (10.19)
. (10.19)Случайная величина  называется непрерывной, если существует неотрицательная функция такая, что
называется непрерывной, если существует неотрицательная функция такая, что
 называется непрерывной, если существует неотрицательная функция такая, что
называется непрерывной, если существует неотрицательная функция такая, что  . (10.20)
. (10.20)Свойства плотности распределения
1.  .
.
 .
.2.  . (10.21)
. (10.21)
 . (10.21)
. (10.21)3.  . (10.22)
. (10.22)
 . (10.22)
. (10.22)Вероятность того, что  примет значение из промежутка
примет значение из промежутка  находят по формулам:
находят по формулам:
1) ; (10.23)
; (10.23)
 примет значение из промежутка
примет значение из промежутка  находят по формулам:
находят по формулам: 1)
 ; (10.23)
; (10.23)2)  . (10.24)
. (10.24)
 . (10.24)
. (10.24)Числовые характеристики случайной величины
1. Математическое ожидание  – это среднее значение величины
– это среднее значение величины  или центр ее распределения.
или центр ее распределения.
 – это среднее значение величины
– это среднее значение величины  или центр ее распределения.
или центр ее распределения.Математическое ожидание непрерывной  с плотностью распределения
с плотностью распределения  находят по формулам:
находят по формулам:
1) , (10.26)
, (10.26)
 с плотностью распределения
с плотностью распределения  находят по формулам:
находят по формулам: 1)
 , (10.26)
, (10.26)если все значения  принадлежат отрезку
принадлежат отрезку ![[\alpha ,\beta ] LaTeX formula: [\alpha ,\beta ]](https://helpy.quali.me/uploads/formulas/7eab532e635fe1149f8b73e39315c79278ac4e4d.1.1.png) ;
;
 принадлежат отрезку
принадлежат отрезку ![[\alpha ,\beta ] LaTeX formula: [\alpha ,\beta ]](https://helpy.quali.me/uploads/formulas/7eab532e635fe1149f8b73e39315c79278ac4e4d.1.1.png) ;
;2)  , (10.26.1)
, (10.26.1)
 , (10.26.1)
, (10.26.1)если все значения  принадлежат промежутку
принадлежат промежутку 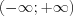 .
.
 принадлежат промежутку
принадлежат промежутку 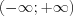 .
.2. Дисперсия или рассеивание  – это математическое ожидание квадрата отклонения величины
– это математическое ожидание квадрата отклонения величины  от ее математического ожидания:
от ее математического ожидания:
 – это математическое ожидание квадрата отклонения величины
– это математическое ожидание квадрата отклонения величины  от ее математического ожидания:
от ее математического ожидания:  , (10.27)
, (10.27)Дисперсию непрерывной  с плотностью распределения
с плотностью распределения  находят по формулам:
находят по формулам:
 с плотностью распределения
с плотностью распределения  находят по формулам:
находят по формулам:1)  , (10.30)
, (10.30)
 , (10.30)
, (10.30)если все значения  принадлежат отрезку
принадлежат отрезку ![[\alpha ,\beta ] LaTeX formula: [\alpha ,\beta ]](https://helpy.quali.me/uploads/formulas/7eab532e635fe1149f8b73e39315c79278ac4e4d.1.1.png) ;
;
 принадлежат отрезку
принадлежат отрезку ![[\alpha ,\beta ] LaTeX formula: [\alpha ,\beta ]](https://helpy.quali.me/uploads/formulas/7eab532e635fe1149f8b73e39315c79278ac4e4d.1.1.png) ;
;2)  , (10.30.1)
, (10.30.1)
 , (10.30.1)
, (10.30.1)если все значения  принадлежат промежутку
принадлежат промежутку 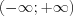 .
.
 принадлежат промежутку
принадлежат промежутку 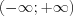 .
.3. Среднеквадратическое отклонение  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле: . (10.31)
. (10.31)Пример 1. Известна функция распределения случайной величины 
Найдите вероятность того, что примет значение из промежутка
примет значение из промежутка  .
.

Найдите вероятность того, что
 примет значение из промежутка
примет значение из промежутка  .
.Решение.
При функция распределения имеет вид
функция распределения имеет вид  .
.
При функция распределения имеет вид
функция распределения имеет вид  .
.
Согласно формуле 10.23 получим:
При
 функция распределения имеет вид
функция распределения имеет вид  .
. При
 функция распределения имеет вид
функция распределения имеет вид  .
. Согласно формуле 10.23 получим:
 .
.Ответ:  .
.
 .
.Пример 2. Известна функция  плотности распределения вероятностей случайной величины. Найдите вероятность того, что
плотности распределения вероятностей случайной величины. Найдите вероятность того, что  примет значение из промежутка
примет значение из промежутка ![[-0,5\pi;0] LaTeX formula: [-0,5\pi;0]](https://helpy.quali.me/uploads/formulas/9718075cb1abc954d7c56835eb80c3a5f5d6b361.1.1.png) .
.
 плотности распределения вероятностей случайной величины. Найдите вероятность того, что
плотности распределения вероятностей случайной величины. Найдите вероятность того, что  примет значение из промежутка
примет значение из промежутка ![[-0,5\pi;0] LaTeX formula: [-0,5\pi;0]](https://helpy.quali.me/uploads/formulas/9718075cb1abc954d7c56835eb80c3a5f5d6b361.1.1.png) .
. Решение. Поскольку при  функция плотности вероятностей имеет вид
функция плотности вероятностей имеет вид  , то согласно формуле 10.24 получим:
, то согласно формуле 10.24 получим:
 функция плотности вероятностей имеет вид
функция плотности вероятностей имеет вид  , то согласно формуле 10.24 получим:
, то согласно формуле 10.24 получим: 

 .
.Ответ:  .
.
 .
.Вероятность того, что непрерывная  примет значения из промежутков
примет значения из промежутков  ,
, ![(\alpha ;\beta ] LaTeX formula: (\alpha ;\beta ]](https://helpy.quali.me/uploads/formulas/57fdf674478f9f59a2b66913771a556a8bdc257c.1.1.png) и
и ![[\alpha ;\beta ] LaTeX formula: [\alpha ;\beta ]](https://helpy.quali.me/uploads/formulas/b56ad145412b672e844eb88455d04c41dca8204e.1.1.png) также находят по формуле 10.23, поскольку вероятность того, что
также находят по формуле 10.23, поскольку вероятность того, что  примет только одно значение из заданного промежутка, равна нулю:
примет только одно значение из заданного промежутка, равна нулю:
 ,
,  .
.
 примет значения из промежутков
примет значения из промежутков  ,
, ![(\alpha ;\beta ] LaTeX formula: (\alpha ;\beta ]](https://helpy.quali.me/uploads/formulas/57fdf674478f9f59a2b66913771a556a8bdc257c.1.1.png) и
и ![[\alpha ;\beta ] LaTeX formula: [\alpha ;\beta ]](https://helpy.quali.me/uploads/formulas/b56ad145412b672e844eb88455d04c41dca8204e.1.1.png) также находят по формуле 10.23, поскольку вероятность того, что
также находят по формуле 10.23, поскольку вероятность того, что  примет только одно значение из заданного промежутка, равна нулю:
примет только одно значение из заданного промежутка, равна нулю: ,
,  .
. 




 .
. 
 .
.

 ;
; 