Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
1. Прямоугольная декартова система координат. 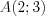 ,
, .png) ,
, .png) ,
, .png) ,
, .png) .
. 
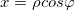 (3.23),
(3.23), 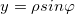 ; (3.24)
; (3.24)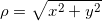 (3.25),
(3.25), 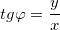 . (3.26)
. (3.26)
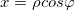 (3.27),
(3.27), 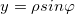 (3.28),
(3.28), 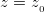 ; (3.29)
; (3.29)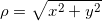 (3.30),
(3.30), 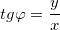 (3.31),
(3.31), 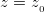 . (3.32)
. (3.32)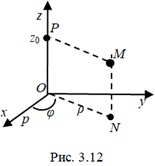
 (3.33) ,
(3.33) ,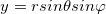 (3.34),
(3.34), 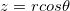 ; (3.35)!!!!!!!!!!!!!!!!!!!!!!!!!!1
; (3.35)!!!!!!!!!!!!!!!!!!!!!!!!!!1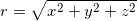 (3.36),
(3.36), 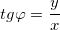 (3.37),
(3.37), 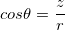 . (3.38)
. (3.38) 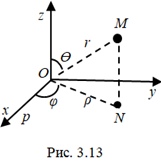
1.1. В двумерном пространстве .png) расположим две координатные прямые
расположим две координатные прямые  и
и  так, чтобы они пересекались под прямым углом (рис. 3.8). Прямую
так, чтобы они пересекались под прямым углом (рис. 3.8). Прямую  называют осью абсцисс, а прямую
называют осью абсцисс, а прямую  — осью ординат. Каждой точке координатной плоскости соответствует пара чисел
— осью ординат. Каждой точке координатной плоскости соответствует пара чисел 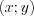 , которые называют координатами точки на плоскости.
, которые называют координатами точки на плоскости.
.png) расположим две координатные прямые
расположим две координатные прямые  и
и  так, чтобы они пересекались под прямым углом (рис. 3.8). Прямую
так, чтобы они пересекались под прямым углом (рис. 3.8). Прямую  называют осью абсцисс, а прямую
называют осью абсцисс, а прямую  — осью ординат. Каждой точке координатной плоскости соответствует пара чисел
— осью ординат. Каждой точке координатной плоскости соответствует пара чисел 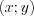 , которые называют координатами точки на плоскости.
, которые называют координатами точки на плоскости. Н а п р и м е р , на рисунке 3.8 в прямоугольной системе координат построены точки:
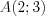 ,
, .png) ,
, .png) ,
, .png) ,
, .png) .
. 1.2. Через некоторую точку  трехмерного пространства
трехмерного пространства .png) проведем три попарно перпендикулярные координатные прямые:
проведем три попарно перпендикулярные координатные прямые:  — ось абсцисс,
— ось абсцисс,  — ось ординат и
— ось ординат и 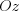 — ось аппликат (рис. 3.9). Каждой точке в пространстве соответствует три числа
— ось аппликат (рис. 3.9). Каждой точке в пространстве соответствует три числа  ,
,  и
и  , которые называют координатами точки в пространстве. Записывают:
, которые называют координатами точки в пространстве. Записывают: .png) .
.
 трехмерного пространства
трехмерного пространства .png) проведем три попарно перпендикулярные координатные прямые:
проведем три попарно перпендикулярные координатные прямые:  — ось абсцисс,
— ось абсцисс,  — ось ординат и
— ось ординат и 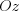 — ось аппликат (рис. 3.9). Каждой точке в пространстве соответствует три числа
— ось аппликат (рис. 3.9). Каждой точке в пространстве соответствует три числа  ,
,  и
и  , которые называют координатами точки в пространстве. Записывают:
, которые называют координатами точки в пространстве. Записывают: .png) .
.Н а п р и м е р, на рисунке 3.9 в прямоугольной декартовой системе координат построены точки: .png) ,
, .png) и
и .png) .
.
.png) ,
, .png) и
и .png) .
.
2. Полярная система координат.
Полярная система координат на плоскости определяется точкой  (полюс), лучом
(полюс), лучом .png) (полярная ось), масштабным отрезком
(полярная ось), масштабным отрезком .png) , направлением отсчета углов (рис. 3.10).
, направлением отсчета углов (рис. 3.10).
 (полюс), лучом
(полюс), лучом .png) (полярная ось), масштабным отрезком
(полярная ось), масштабным отрезком .png) , направлением отсчета углов (рис. 3.10).
, направлением отсчета углов (рис. 3.10).Полярными координатами точки  , не совпадающей с полюсом, называют полярный радиус
, не совпадающей с полюсом, называют полярный радиус .png) (расстояние от точки
(расстояние от точки  до полюса) и полярный угол
до полюса) и полярный угол 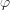 ( угол между полярной осью
( угол между полярной осью .png) и лучом
и лучом 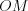 .
.
 , не совпадающей с полюсом, называют полярный радиус
, не совпадающей с полюсом, называют полярный радиус .png) (расстояние от точки
(расстояние от точки  до полюса) и полярный угол
до полюса) и полярный угол 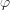 ( угол между полярной осью
( угол между полярной осью .png) и лучом
и лучом 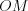 .
. Записывают: .png) , где
, где .png) ,
, .png) .
.
.png) , где
, где .png) ,
, .png) .
.Связь между декартовыми координатами  и
и  точки
точки  и ее полярными координатами
и ее полярными координатами .png) и
и 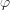 (рис. 3.11) выражается формулами:
(рис. 3.11) выражается формулами:
 и
и  точки
точки  и ее полярными координатами
и ее полярными координатами .png) и
и 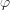 (рис. 3.11) выражается формулами:
(рис. 3.11) выражается формулами: 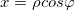 (3.23),
(3.23), 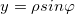 ; (3.24)
; (3.24)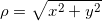 (3.25),
(3.25), 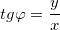 . (3.26)
. (3.26)
3. Цилиндрическая система координат.
Цилиндрическими координатами точки  (рис. 3.12) называют числа
(рис. 3.12) называют числа .png) ,
, 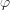 и
и .png) , где
, где .png) и
и 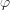 — полярные координаты точки
— полярные координаты точки  ,
, .png) — длина отрезка
— длина отрезка 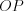 , точка
, точка  — проекция точки
— проекция точки  на плоскость
на плоскость .png) , точка
, точка  — проекция точки
— проекция точки  на ось
на ось 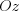 .
.
 (рис. 3.12) называют числа
(рис. 3.12) называют числа .png) ,
, 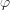 и
и .png) , где
, где .png) и
и 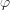 — полярные координаты точки
— полярные координаты точки  ,
, .png) — длина отрезка
— длина отрезка 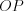 , точка
, точка  — проекция точки
— проекция точки  на плоскость
на плоскость .png) , точка
, точка  — проекция точки
— проекция точки  на ось
на ось 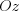 .
.Записывают: .png) , где
, где .png) ,
, .png) .
.
.png) , где
, где .png) ,
, .png) .
.Связь между декартовыми координатами  ,
,  и
и  точки
точки  и ее цилиндрическими координатами
и ее цилиндрическими координатами .png) ,
, 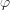 и
и .png) выражается формулами:
выражается формулами:
 ,
,  и
и  точки
точки  и ее цилиндрическими координатами
и ее цилиндрическими координатами .png) ,
, 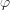 и
и .png) выражается формулами:
выражается формулами: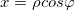 (3.27),
(3.27), 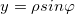 (3.28),
(3.28), 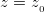 ; (3.29)
; (3.29)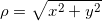 (3.30),
(3.30), 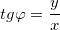 (3.31),
(3.31), 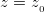 . (3.32)
. (3.32)
4. Сферическая система координат.
Сферическими координатами точки  (рис 3.13) называют числа
(рис 3.13) называют числа  ,
, .png) и
и 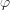 , где
, где  — длина отрезка
— длина отрезка 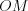 ,
, .png) — угол между отрезком
— угол между отрезком 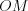 и осью
и осью 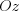 ,
, 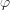 — угол, на который необходимо повернуть ось
— угол, на который необходимо повернуть ось  против часовой стрелки со стороны положительного направления оси
против часовой стрелки со стороны положительного направления оси 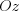 , чтобы она совпала с лучом
, чтобы она совпала с лучом .png) .
.
 (рис 3.13) называют числа
(рис 3.13) называют числа  ,
, .png) и
и 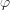 , где
, где  — длина отрезка
— длина отрезка 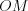 ,
, .png) — угол между отрезком
— угол между отрезком 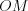 и осью
и осью 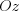 ,
, 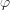 — угол, на который необходимо повернуть ось
— угол, на который необходимо повернуть ось  против часовой стрелки со стороны положительного направления оси
против часовой стрелки со стороны положительного направления оси 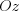 , чтобы она совпала с лучом
, чтобы она совпала с лучом .png) .
. Записывают: .png) , где
, где .png) ,
, 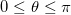 ,
, .png) .
.
.png) , где
, где .png) ,
, 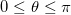 ,
, .png) .
.Связь между декартовыми координатами  ,
,  и
и  точки
точки  и ее сферическими координатами
и ее сферическими координатами  ,
, .png) и
и 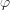 выражается формулами:
выражается формулами:
 ,
,  и
и  точки
точки  и ее сферическими координатами
и ее сферическими координатами  ,
, .png) и
и 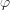 выражается формулами:
выражается формулами: (3.33) ,
(3.33) ,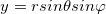 (3.34),
(3.34), 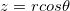 ; (3.35)!!!!!!!!!!!!!!!!!!!!!!!!!!1
; (3.35)!!!!!!!!!!!!!!!!!!!!!!!!!!1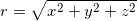 (3.36),
(3.36), 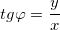 (3.37),
(3.37), 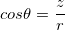 . (3.38)
. (3.38) 
Пример 1. Найдите декартовы координаты точки .png) , заданной в полярной системе координат.
, заданной в полярной системе координат..png) ;
; .png)
.png) ;
; .png) ;
; .png) .
..png) ;
;.png) ;
;.png) .
..png) ,
, 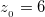 .
..png) , откуда
, откуда .png) , так как проекция точки
, так как проекция точки  на плоскость
на плоскость .png) находится во второй четверти координатной плоскости.
находится во второй четверти координатной плоскости.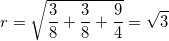 .
.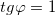 , откуда
, откуда 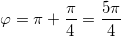 , так как проекция точки
, так как проекция точки  на плоскость
на плоскость 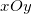 находится в третьей четверти координатной плоскости.
находится в третьей четверти координатной плоскости.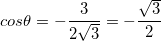 , откуда
, откуда 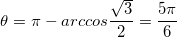 .
.
.png) , заданной в полярной системе координат.
, заданной в полярной системе координат..png) ;
; .png)
Ответ: .png) .
.
.png) .
.Пример 2. Найдите декартовы координаты точки .png) , заданной в цилиндрической системе координат.
, заданной в цилиндрической системе координат.
.png) , заданной в цилиндрической системе координат.
, заданной в цилиндрической системе координат..png) ;
; .png) ;
; .png) .
.Ответ: .png) .
.
.png) .
.Пример 3. Найдите декартовы координаты точки .png) , заданной в сферической системе координат.
, заданной в сферической системе координат.
.png) , заданной в сферической системе координат.
, заданной в сферической системе координат..png) ;
;.png) ;
;.png) .
.Ответ: .png) .
.
.png) .
.Пример 4. Найдите цилиндрические координаты точки .png) , заданной в декартовой системе координат.
, заданной в декартовой системе координат.
.png) , заданной в декартовой системе координат.
, заданной в декартовой системе координат.Решение. Согласно условию задачи 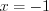 ,
, .png) ,
, .png) .
.
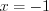 ,
, .png) ,
, .png) .
..png) ,
, 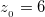 .
.2. По формуле 3.31 получим:
.png) , откуда
, откуда .png) , так как проекция точки
, так как проекция точки  на плоскость
на плоскость .png) находится во второй четверти координатной плоскости.
находится во второй четверти координатной плоскости.Ответ: .png) .
.
.png) .
.Пример 5. Найдите сферические координаты точки 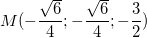 , заданной в декартовой системе координат.
, заданной в декартовой системе координат.
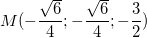 , заданной в декартовой системе координат.
, заданной в декартовой системе координат. Решение. Согласно условию задачи 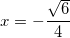 ,
, 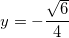 ,
, 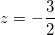 .
.
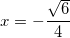 ,
, 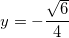 ,
, 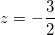 .
.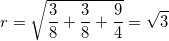 .
.2. По формуле 3.37 получим:
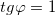 , откуда
, откуда 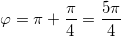 , так как проекция точки
, так как проекция точки  на плоскость
на плоскость 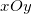 находится в третьей четверти координатной плоскости.
находится в третьей четверти координатной плоскости.3. По формуле 3.38 получим:
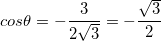 , откуда
, откуда 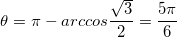 .
.Ответ:  .
.
 .
.Так как в полярной, цилиндрической и сферической системах координат .png) то:
то:
.png) то:
то:1) если 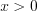 и
и 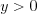 , то
, то .png) ;
;
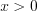 и
и 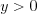 , то
, то .png) ;
;2) если .png) , а
, а 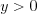 , то
, то .png) ;
;
.png) , а
, а 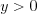 , то
, то .png) ;
;3) если .png) и
и .png) , то
, то .png) ;
;
.png) и
и .png) , то
, то .png) ;
;4) если 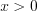 , а
, а .png) , то
, то .png) .
.
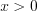 , а
, а .png) , то
, то .png) .
.

.png)
.png) , то по формулам
, то по формулам .png) ,
, .png) ,
, .png) , то по формулам
, то по формулам .png) ,
, 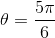 ,
, .png) , то по формулам
, то по формулам