Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ;
; 
 ,
,  .
.  ;
; 
 ,
,  .
. ;
; 
 .
.  ;
; 
 .
. ;
; 
 .
. . ( 12.1)
. ( 12.1) . (12.2)
. (12.2) (12.3)
(12.3) . (12.4)
. (12.4)
 ; (12.2.1)
; (12.2.1) (12.3.1)
(12.3.1)  . (12.4.1)
. (12.4.1)
 . (12.18)
. (12.18) . (12.19)
. (12.19) . (12.20)
. (12.20) . (12.21)
. (12.21)

 ; (12.22)
; (12.22) ; (12.23)
; (12.23) (12.24)
(12.24) . (12.25)
. (12.25) .
. ; (12.23.1)
; (12.23.1) (12.24.1)
(12.24.1) . (12.25.1)
. (12.25.1)  (12.26)
(12.26) ,
,  , …,
, …,  , …,
, …,  .
.
 ;
; 

 ;
;


 ;
;  ;
;  ;
;  ;
;  ;
;  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
. ;
;  ;
;  ;
;  ;
;  ;
;  .
. 
 ;
;

 .
.  ;
; 
 ;
; 

 ,
,  ,
,  ,
,  ,
,  .
.
Предпочтительный вид модели ЗЛП
Каноническая модель ЗЛП имеет предпочтительный вид, если в каждом из уравнений системы ограничений присутствует предпочтительная переменная.
Переменная называется предпочтительной, если она присутствует только в одном из уравнений системы ограничений и только с коэффициентом, равным единице.
Н а п р и м е р, рассмотрим задачу:
 ;
; 
 ,
,  .
.Переменные  ,
,  и
и  являются предпочтительными.
являются предпочтительными.
 ,
,  и
и  являются предпочтительными.
являются предпочтительными. Если в канонической модели задачи отсутствуют предпочтительные переменные, то вводим неотрицательные искусственные переменные. В целевую функции эти переменные в случае ее максимизации вводим с коэффициентом, равным  , а в случае минимизации – с коэффициентом, равным
, а в случае минимизации – с коэффициентом, равным  .
.
 , а в случае минимизации – с коэффициентом, равным
, а в случае минимизации – с коэффициентом, равным  .
. Н а п р и м е р, рассмотрим задачу:
 ;
; 
 ,
,  .
.Поскольку в третьем уравнении системы ограничений отсутствует предпочтительная переменная, то вводим искусственную переменную  . Получим:
. Получим:
 . Получим:
. Получим:  ;
; 
 .
. Н а п р и м е р, рассмотрим задачу:
 ;
; 
 .
.Поскольку в первых двух уравнениях системы ограничений отсутствуют предпочтительные переменные, то вводим искусственные переменные  и
и  . Получим:
. Получим:
 и
и  . Получим:
. Получим:  ;
; 
 .
.Построение начального опорного плана задачи
Рассмотрим задачу:
 . ( 12.1)
. ( 12.1) . (12.2)
. (12.2) (12.3)
(12.3) . (12.4)
. (12.4)1. Приведем математическую модель задачи к каноническому и предпочтительному виду.
Введем дополнительные переменные ,
,  , ... ,
, ... ,  и получим:
и получим:
Введем дополнительные переменные
 ,
,  , ... ,
, ... ,  и получим:
и получим: 
 ; (12.2.1)
; (12.2.1) (12.3.1)
(12.3.1)  . (12.4.1)
. (12.4.1)В нашем случае дополнительные переменные являются и предпочтительными.
2. Предпочтительные переменные являются базисными, а остальные переменные – свободными. Свободные переменные считаем равными нулю.
Чтобы найти значения базисных переменных, необходимо в систему ограничений подставить значения свободных переменных.
Получим: свободные переменные ,
, 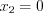 , …,
, …,  ;
;
базисные переменные ,
,  , …,
, …,  .
.
Чтобы найти значения базисных переменных, необходимо в систему ограничений подставить значения свободных переменных.
Получим: свободные переменные
 ,
, 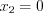 , …,
, …,  ;
; базисные переменные
 ,
,  , …,
, …,  .
.3. Составляем симплексную таблицу нулевой итерации:
4. Заполняем индексную строку.
Оценка целевой функции (значение целевой функции):
 . (12.18)
. (12.18)Оценки переменных:
 . (12.19)
. (12.19)Критерий оптимальности опорного плана задачи:
а) если при максимизации целевой функции все оценки переменных неотрицательные, то план оптимален;
б) если при минимизации целевой функции все оценки переменных неположительные, то план оптимален.
Переход к не худшему плану ЗЛП
Если опорный план задачи не удовлетворяет критерию оптимальности, то выполняем следующие действия.
1. Выбираем наихудшую оценку переменной. В случае максимизации целевой функции – наименьшую отрицательную, а в случае минимизации – наибольшую положительную. Столбец, в которой находится эта переменная, называется разрешающим.
2. Для каждой базисной переменной составляем симплексные отношения – находим отношения элементов столбца  и соответствующих элементов разрешающего столбца (отрицательные элементы разрешающего столбца и элементы, равные нулю, не образуют симплексных отношений):
и соответствующих элементов разрешающего столбца (отрицательные элементы разрешающего столбца и элементы, равные нулю, не образуют симплексных отношений):
 и соответствующих элементов разрешающего столбца (отрицательные элементы разрешающего столбца и элементы, равные нулю, не образуют симплексных отношений):
и соответствующих элементов разрешающего столбца (отрицательные элементы разрешающего столбца и элементы, равные нулю, не образуют симплексных отношений):  . (12.20)
. (12.20)Из полученных отношений выбираем наименьшее. Строку, которой соответствует это отношение, называем разрешающей. Элемент, который находится на пересечении разрешающих столбца и строки, называется разрешающим элементом  .
.
 .
. 3. Переходим к первой итерации симплексной таблицы.
Вносим изменения в базис: переменную, находящуюся в разрешающей строке нулевой итерации заменяем переменной из разрешающего столбца.
Все элементы разрешающей строки делим на разрешающий элемент и записываем в строку первой итерации (номер строки совпадает с номером строки нулевой итерации).
Все остальные элементы столбца, номер которого совпадает с номером разрешающего столбца нулевой итерации, считаем равными нулю.
Остальные элементы таблицы находим по правилу прямоугольника (рис. 12.5):
 . (12.21)
. (12.21)
Если выполняется критерий оптимальности нового плана задачи, то данная задача решена. В противном случае аналогично заполняем таблицу второй итерации.
Постановка двойственной задачи
Рассмотрим задачу 12.1 – 12.2 – 12.3 – 12.24 об определении оптимального плана выпуска продукции, данные которой приведены в таблице:
Введем новые переменные  ,
,  , …,
, …,  , которые назовем оценками ресурсов.
, которые назовем оценками ресурсов.
Оценки должны быть установлены исходя из следующих соображений:
 ,
,  , …,
, …,  , которые назовем оценками ресурсов.
, которые назовем оценками ресурсов. Оценки должны быть установлены исходя из следующих соображений:
1) общая стоимость ресурсов должна быть минимизирована;
2) в случае продажи ресурса выручка должна быть не меньше стоимости продукции при организации производства.
Математическая модель задачи примет вид:
 ; (12.22)
; (12.22) ; (12.23)
; (12.23) (12.24)
(12.24) . (12.25)
. (12.25)Задачи 12.1 – 12.2 – 12.3 – 12.4 и 12.22 – 12.23 – 12.24 - 12.25 называют парой симметричных двойственных задач.
Если одна из двойственных задач имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем оптимальные значения целевых функций совпадают:
 .
. ; (12.23.1)
; (12.23.1) (12.24.1)
(12.24.1) . (12.25.1)
. (12.25.1)Установим соответствие между переменными двойственных задач:
 (12.26)
(12.26)Значения переменных  равны оценкам переменных
равны оценкам переменных  :
:
 равны оценкам переменных
равны оценкам переменных  :
: ,
,  , …,
, …,  , …,
, …,  .
. 1) основные переменные  ,
,  , …,
, …,  показывают объемы выпуска продукции;
показывают объемы выпуска продукции;
 ,
,  , …,
, …,  показывают объемы выпуска продукции;
показывают объемы выпуска продукции; 2) дополнительные переменные  ,
,  , …,
, …,  показывают остатки ресурсов.
показывают остатки ресурсов.
 ,
,  , …,
, …,  показывают остатки ресурсов.
показывают остатки ресурсов.1) основные переменные  ,
,  , …,
, …,  показывают, насколько увеличится значение целевой функции, при использовании в процессе производства дополнительной единицы соответствующего ресурса;
показывают, насколько увеличится значение целевой функции, при использовании в процессе производства дополнительной единицы соответствующего ресурса;
 ,
,  , …,
, …,  показывают, насколько увеличится значение целевой функции, при использовании в процессе производства дополнительной единицы соответствующего ресурса;
показывают, насколько увеличится значение целевой функции, при использовании в процессе производства дополнительной единицы соответствующего ресурса; 2) дополнительные переменные  ,
,  , …,
, …,  показывают, насколько уменьшится значение целевой функции при условии дополнительного выпуска одной единицы соответствующей продукции.
показывают, насколько уменьшится значение целевой функции при условии дополнительного выпуска одной единицы соответствующей продукции.
 ,
,  , …,
, …,  показывают, насколько уменьшится значение целевой функции при условии дополнительного выпуска одной единицы соответствующей продукции.
показывают, насколько уменьшится значение целевой функции при условии дополнительного выпуска одной единицы соответствующей продукции.Пример 1. Решите симплексным методом задачу линейного программирования:
 ;
; 

Выполните послеоптимизацонный анализ.
Решение. Приведем модель задачи к каноническому и предпочтительному виду:
 ;
; 
Базисные переменные:  ,
,  .
.
 ,
,  .
.Свободные переменные:  ,
, 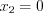 ,
, 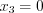 ,
,  .
.
 ,
, 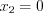 ,
, 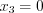 ,
,  .
.Составим симплексную таблицу и выполним симплексные преобразования:
Пояснения к нулевой итерации.
По формуле 12.19 получим:
 ;
;  ;
;  ;
;  ;
;  ;
;  .
.Поскольку присутствуют отрицательные оценки переменных, то опорный план задачи не оптимальный. В качестве разрешающего столбца выбираем столбец  , так как переменная
, так как переменная  имеет наименьшую оценку.
имеет наименьшую оценку.
 , так как переменная
, так как переменная  имеет наименьшую оценку.
имеет наименьшую оценку. По формуле 12.20 находим симплексные отношения:
 ;
;  .
.
Так как , то первая строка будет разрешающей. Разрешающий элемент
, то первая строка будет разрешающей. Разрешающий элемент  .
.
 ;
;  .
. Так как
 , то первая строка будет разрешающей. Разрешающий элемент
, то первая строка будет разрешающей. Разрешающий элемент  .
.Пояснения к первой итерации.
Вносим изменения в базис: переменную заменяем переменной
заменяем переменной  .
.
Все элементы разрешающей строки нулевой итерации делим на и результаты записываем в первую строку первой итерации.
и результаты записываем в первую строку первой итерации.
Элемент считаем равным нулю.
считаем равным нулю.
Остальные элементы второй строки находим по формуле 12.21 (рис. 12.5):
Вносим изменения в базис: переменную
 заменяем переменной
заменяем переменной  .
. Все элементы разрешающей строки нулевой итерации делим на
 и результаты записываем в первую строку первой итерации.
и результаты записываем в первую строку первой итерации. Элемент
 считаем равным нулю.
считаем равным нулю. Остальные элементы второй строки находим по формуле 12.21 (рис. 12.5):
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.По формуле 12.19 получим:
 ;
;  ;
;  ;
;  ;
;  ;
;  .
.Поскольку присутствуют отрицательные оценки переменных, то опорный план задачи не оптимальный. В качестве разрешающего столбца выбираем столбец  , так как переменная
, так как переменная  имеет наименьшую оценку.
имеет наименьшую оценку.
 , так как переменная
, так как переменная  имеет наименьшую оценку.
имеет наименьшую оценку. По формуле 12.20 находим симплексные отношения:
 ;
;  .
.
Так как , то вторая строка будет разрешающей. Разрешающий элемент
, то вторая строка будет разрешающей. Разрешающий элемент  .
.
 ;
;  .
. Так как
 , то вторая строка будет разрешающей. Разрешающий элемент
, то вторая строка будет разрешающей. Разрешающий элемент  .
.Вторая итерация.
Аналогично заполняем таблицу второй итерации.
Поскольку все оценки переменных неотрицательные, то опорный план второй итерации оптимальный:
 ;
;  ден. ед.
ден. ед.
Аналогично заполняем таблицу второй итерации.
Поскольку все оценки переменных неотрицательные, то опорный план второй итерации оптимальный:
 ;
;  ден. ед.
ден. ед.Послеоптимизационный анализ
На основании 12.26 установим соответствие между двойственными переменными:

Следовательно,
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.План выпуска продукции: продукцию первого вида выпускаем в объеме  ед, второго вида – в объеме
ед, второго вида – в объеме  ед., продукцию третьего и четвертого видов выпускать не следует.
ед., продукцию третьего и четвертого видов выпускать не следует.
 ед, второго вида – в объеме
ед, второго вида – в объеме  ед., продукцию третьего и четвертого видов выпускать не следует.
ед., продукцию третьего и четвертого видов выпускать не следует.Оптимальное значение целевой функции (максимальная выручка) составит  ден. ед.
ден. ед.
 ден. ед.
ден. ед.Оценки ресурсов: каждая использованная единица первого ресурса увеличивает доход на  ден. ед., а каждая единица второго ресурса – на
ден. ед., а каждая единица второго ресурса – на  ден. ед. Первая и вторая продукция не убыточные. Выпуск одной единицы продукции третьего вида приносит убыток в размере
ден. ед. Первая и вторая продукция не убыточные. Выпуск одной единицы продукции третьего вида приносит убыток в размере  ден. ед., а четвертого – в размере
ден. ед., а четвертого – в размере  ден. ед.
ден. ед.
 ден. ед., а каждая единица второго ресурса – на
ден. ед., а каждая единица второго ресурса – на  ден. ед. Первая и вторая продукция не убыточные. Выпуск одной единицы продукции третьего вида приносит убыток в размере
ден. ед. Первая и вторая продукция не убыточные. Выпуск одной единицы продукции третьего вида приносит убыток в размере  ден. ед., а четвертого – в размере
ден. ед., а четвертого – в размере  ден. ед.
ден. ед. Пример 2. Решите симплексным методом задачу линейного программирования:
 ;
; 
 .
. Решение. Приведем модель задачи к каноническому виду:
 ;
; 
Приведем модель задачи к предпочтительному виду:
 ;
; 
Базисные переменные:  ,
,  .
.
 ,
,  .
.Свободные переменные:  ,
,  ,
,  .
.
 ,
,  ,
,  .
.Составим симплексную таблицу и выполним симплексные преобразования:
Пояснения к нулевой итерации.
Поскольку присутствуют положительные оценки переменных, то опорный план задачи не оптимальный.
В качестве разрешающего столбца выбираем столбец , так как переменная
, так как переменная  имеет наибольшую оценку.
имеет наибольшую оценку.
В качестве разрешающего столбца выбираем столбец
 , так как переменная
, так как переменная  имеет наибольшую оценку.
имеет наибольшую оценку. Так как  , то первая строка будет разрешающей. Разрешающий элемент
, то первая строка будет разрешающей. Разрешающий элемент  .
.
 , то первая строка будет разрешающей. Разрешающий элемент
, то первая строка будет разрешающей. Разрешающий элемент  .
.Пояснения к первой итерации.
Вносим изменения в базис: переменную заменяем переменной
заменяем переменной  .
.
Все элементы разрешающей строки нулевой итерации делим на и результаты записываем в первую строку первой итерации.
и результаты записываем в первую строку первой итерации.
Элемент считаем равным нулю.
считаем равным нулю.
Остальные элементы второй строки находим по формуле 12.21 (рис. 12.5):
Вносим изменения в базис: переменную
 заменяем переменной
заменяем переменной  .
. Все элементы разрешающей строки нулевой итерации делим на
 и результаты записываем в первую строку первой итерации.
и результаты записываем в первую строку первой итерации. Элемент
 считаем равным нулю.
считаем равным нулю. Остальные элементы второй строки находим по формуле 12.21 (рис. 12.5):
 ,
,  ,
,  ,
,  ,
,  .
.Поскольку оценка переменной  положительная, то опорный план задачи не оптимальный.
положительная, то опорный план задачи не оптимальный.
В качестве разрешающего столбца выбираем столбец .
.
 положительная, то опорный план задачи не оптимальный.
положительная, то опорный план задачи не оптимальный. В качестве разрешающего столбца выбираем столбец
 .
. Так как отрицательный элемент разрешающего столбца не образует симплексного отношения, то вторая строка будет разрешающей. Разрешающий элемент  .
.
 .
.Вторая итерация. Аналогично заполняем таблицу второй итерации.
Поскольку все оценки переменных неположительные, то опорный план второй итерации оптимальный:
 ,
,  ,
,  .
.
Поскольку все оценки переменных неположительные, то опорный план второй итерации оптимальный:
 ,
,  ,
,  .
. Ответ:  ;
;  .
.
 ;
;  .
.1. Оценки базисных переменных всегда равны нулю.
2. Отрицательные элементы разрешающего столбца и элементы, равные нулю, не образуют симплексных отношений.
3. Задача с искусственным базисом называется М-задачей. При решении М-задачи по мере выведения искусственных переменных из базиса они выводятся и из симплексной таблицы.
4. Графическое решение Примера 2 приведено в разделе Графический метод / Примеры.

















