Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 .
.




























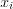 - произвольные,
- произвольные, 














 – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 
 – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 
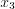 – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 

 или
или 








Математическое программирование – область математики, разрабатывающая теорию и численные методы решения задач на экстремум функции многих переменных с ограничениями на область определения этих переменных.
Математической моделью задачи называют отражение реальной (производственной, экономической) ситуации в виде функций, уравнений и неравенств.
Линейным программированием (ЛП) называют раздел математического программирования, если все функции математической модели задачи линейные.
К основным видам задач ЛП, как правило, относят: задачи о наилучшем использовании ресурсов, задачи о выборе оптимальных технологий, задачи о размещении заказа, задачи о смесях, задачи о раскрое материалов, транспортные задачи и т. п.
Рассмотрим постановку одной из задач и составим ее математическую модель.
Постановка задачи. Предприятие пытается наладить выпуск n видов продукции:  Для этого оно располагает
Для этого оно располагает  видами ресурсов
видами ресурсов  объемы которых соответственно составляют:
объемы которых соответственно составляют:  Известна прибыль, которую можно получить от реализации одной единицы каждого вида продукции:
Известна прибыль, которую можно получить от реализации одной единицы каждого вида продукции:  Расход
Расход 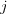 -го вида ресурса на выпуск одной единицы
-го вида ресурса на выпуск одной единицы  -го вида продукции
-го вида продукции 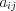 представлен в технологической матрице:
представлен в технологической матрице:
 Для этого оно располагает
Для этого оно располагает  видами ресурсов
видами ресурсов  объемы которых соответственно составляют:
объемы которых соответственно составляют:  Известна прибыль, которую можно получить от реализации одной единицы каждого вида продукции:
Известна прибыль, которую можно получить от реализации одной единицы каждого вида продукции:  Расход
Расход 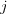 -го вида ресурса на выпуск одной единицы
-го вида ресурса на выпуск одной единицы  -го вида продукции
-го вида продукции 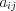 представлен в технологической матрице:
представлен в технологической матрице: .
.Необходимо определить план выпуска продукции, обеспечивающий максимальную прибыль.
Представим данные задачи в таблице:
Составим математическую модель задачи.
План: 



Целевая функция качества:


Система ограничений:


Условия не отрицательности переменных:


Основные виды записи ЗЛП






Каноническая форма записи ЗЛП:







Чтобы привести модель задачи к каноническому виду, при условии, что все правые части неравенств-ограничений неотрицательные, необходимо:
1) к левым частям неравенств типа  прибавить неотрицательные дополнительные переменные, а из левых частей неравенств типа
прибавить неотрицательные дополнительные переменные, а из левых частей неравенств типа  вычесть неотрицательные дополнительные переменные;
вычесть неотрицательные дополнительные переменные;
 прибавить неотрицательные дополнительные переменные, а из левых частей неравенств типа
прибавить неотрицательные дополнительные переменные, а из левых частей неравенств типа  вычесть неотрицательные дополнительные переменные;
вычесть неотрицательные дополнительные переменные;2) в целевую функцию дополнительные переменные ввести с коэффициентами, равными нулю.
Общая форма записи ЗЛП:









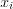 - произвольные,
- произвольные, 

Пример 1. При изготовлении продукции  и
и  используются токарные и фрезерные станки, а также сталь и цветные металлы. На производство единицы продукции
используются токарные и фрезерные станки, а также сталь и цветные металлы. На производство единицы продукции  требуется
требуется  и
и  станко-часов соответственно токарного и фрезерного оборудования, а также
станко-часов соответственно токарного и фрезерного оборудования, а также 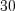 кг стали и
кг стали и  кг цветных металлов. Для производства единицы продукции
кг цветных металлов. Для производства единицы продукции  требуется соответственно
требуется соответственно  и
и  единиц тех же ресурсов. Цех располагает
единиц тех же ресурсов. Цех располагает  и
и  станко-часами оборудования,
станко-часами оборудования,  кг и
кг и  кг металлов. Прибыль от реализации единицы продукции
кг металлов. Прибыль от реализации единицы продукции  составляет
составляет  тыс. ден. ед., а продукции
тыс. ден. ед., а продукции  –
–  тыс. ден. ед. Необходимо определить план выпуска продукции, обеспечивающий максимальную прибыль.
тыс. ден. ед. Необходимо определить план выпуска продукции, обеспечивающий максимальную прибыль.
 и
и  используются токарные и фрезерные станки, а также сталь и цветные металлы. На производство единицы продукции
используются токарные и фрезерные станки, а также сталь и цветные металлы. На производство единицы продукции  требуется
требуется  и
и  станко-часов соответственно токарного и фрезерного оборудования, а также
станко-часов соответственно токарного и фрезерного оборудования, а также 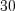 кг стали и
кг стали и  кг цветных металлов. Для производства единицы продукции
кг цветных металлов. Для производства единицы продукции  требуется соответственно
требуется соответственно  и
и  единиц тех же ресурсов. Цех располагает
единиц тех же ресурсов. Цех располагает  и
и  станко-часами оборудования,
станко-часами оборудования,  кг и
кг и  кг металлов. Прибыль от реализации единицы продукции
кг металлов. Прибыль от реализации единицы продукции  составляет
составляет  тыс. ден. ед., а продукции
тыс. ден. ед., а продукции  –
–  тыс. ден. ед. Необходимо определить план выпуска продукции, обеспечивающий максимальную прибыль.
тыс. ден. ед. Необходимо определить план выпуска продукции, обеспечивающий максимальную прибыль. Составьте математическую модель задачи и приведите ее к каноническому виду.
Решение. Составим таблицу данных:



Приведем модель задачи к каноническому виду 12.8 – 12.9 – 12.10 с помощью дополнительных переменных  и
и  .
.
Получим:
 и
и  .
. Получим:


Пример 2. В опытном хозяйстве установили, что откорм животных выгоден тогда, когда животное будет получать в дневном рационе не менее  ед. питательного вещества
ед. питательного вещества  не менее
не менее  ед. вещества
ед. вещества  и не менее
и не менее  ед. вещества
ед. вещества  . Для кормления животных используются три вида корма:
. Для кормления животных используются три вида корма:  и
и  .
.
Составьте математическую модель задачи для определения суточного рациона кормления скота и приведите ее к каноническому виду.
В таблице показано сколько единиц каждого питательного вещества содержит кг корма каждого вида:
кг корма каждого вида:
 ед. питательного вещества
ед. питательного вещества  не менее
не менее  ед. вещества
ед. вещества  и не менее
и не менее  ед. вещества
ед. вещества  . Для кормления животных используются три вида корма:
. Для кормления животных используются три вида корма:  и
и  .
. Составьте математическую модель задачи для определения суточного рациона кормления скота и приведите ее к каноническому виду.
В таблице показано сколько единиц каждого питательного вещества содержит
 кг корма каждого вида:
кг корма каждого вида:план закупки корма: 




Приведем модель задачи к каноническому виду 12.8 – 12.9 – 12.10 с помощью дополнительных переменных и
и  . Получим:
. Получим:
 и
и  . Получим:
. Получим:

Пример 3. В цех распила поступило  бревен длиной
бревен длиной  м. Их необходимо разрезать на заготовки
м. Их необходимо разрезать на заготовки  и
и  длиной соответственно
длиной соответственно  м и
м и  м и составить из них комплекты. В каждый комплект входит
м и составить из них комплекты. В каждый комплект входит  заготовки
заготовки  и
и  заготовки
заготовки  .
.
Составьте математическую модель задачи для определения плана распила бревен, гарантирующего минимизацию отходов, и приведите ее к каноническому виду.
 бревен длиной
бревен длиной  м. Их необходимо разрезать на заготовки
м. Их необходимо разрезать на заготовки  и
и  длиной соответственно
длиной соответственно  м и
м и  м и составить из них комплекты. В каждый комплект входит
м и составить из них комплекты. В каждый комплект входит  заготовки
заготовки  и
и  заготовки
заготовки  .
. Составьте математическую модель задачи для определения плана распила бревен, гарантирующего минимизацию отходов, и приведите ее к каноническому виду.
Решение. Составим таблицу данных:
Составим математическую модель задачи:
План:  где
где
 где
где  – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 
 – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 
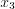 – количество бревен, подлежащих распилу по варианту
– количество бревен, подлежащих распилу по варианту 

Целевая функция: 

Система ограничений:
 или
или 



Прежде, чем приводить модель задачи к каноническому виду, необходимо убедиться (а в случае необходимости выполнить преобразования), что все правые части неравенств-ограничений неотрицательные.
Н а п р и м е р, приведем модель задачи к каноническому виду:


Поскольку правые части первого и третьего неравенств системы ограничений отрицательные, то, умножим эти неравенства на число  и получим:
и получим:
 и получим:
и получим: 



