Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
; (11.32)
; (11.33)
. (11.34)
; (11.35)
; (11.36)
. (11.37)
. (11.38)
Дисперсионный анализ определяется как статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента.
Рассмотрим задачу выявления и оценки степени влияния фактора 
на изменчивость случайной величины 
(полный дисперсионный однофакторный анализ с параллельными испытаниями).
на изменчивость случайной величины (полный дисперсионный однофакторный анализ с параллельными испытаниями).Рассмотрим m уровней фактора , на каждом из которых поставлено по 
испытаний:
, на каждом из которых поставлено по испытаний: Объем выборки: 
.
. Имеет место равенство 
, где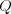 
– общая изменчивость (вариативность) ; 
– сумма изменчивостей внутри уровней;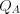 
– изменчивость между уровнями.
, где 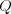– общая изменчивость (вариативность) ; – сумма изменчивостей внутри уровней; 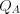– изменчивость между уровнями.1. Вычислим:
; (11.32) ; (11.33) . (11.34)2. Определим:
; (11.35) ; (11.36) . (11.37)3. Найдем критическую точку распределения Фишера:
. (11.38)4. Сравним 
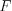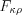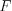и 
:
и 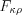: 1) если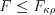 
, то принимаем гипотезу об отсутствии влияния фактора на величину ;
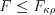, то принимаем гипотезу об отсутствии влияния фактора на величину ; 2) если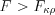 
, то влияние фактора значимо.
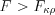, то влияние фактора значимо.Пример. В экспериментальном классе разработаны три варианта методики обучения. Необходимо оценить степень влияния экспериментальной методики обучения на изменчивость уровня математической подготовки учащихся. Результаты промежуточной аттестации приведены в таблице: 
Решение. Все расчеты будем выполнять в таблице:
: 
.
.
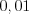найдем критическую точку распределения Фишера: 
