Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
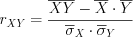 , (11.26)
, (11.26) , (11.2)
, (11.2)  , (11.2.1)
, (11.2.1) , (11.3)
, (11.3)  , (11.3.1)
, (11.3.1) , (11.4)
, (11.4)  , (11.4.1)
, (11.4.1) ; (11.5)
; (11.5)  ; (11.5.1)
; (11.5.1) . (11.27)
. (11.27)



 .
.
Статистической называют зависимость, при которой изменение одной из случайных величин влечет изменение распределения другой.
Статистическую зависимость называют корреляционной, если изменение одной из случайных величин вызывает изменение среднего значения другой.
Коэффициент корреляции показывает тесноту связи между признаками  и
и  .
.
 и
и  .
.Пусть из генеральной совокупности извлечена выборка двумерной случайной величины 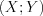 объема
объема
 .
.
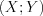 объема
объема  .
.Выборочный коэффициент корреляции находят по формуле:
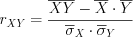 , (11.26)
, (11.26)где
 , (11.2)
, (11.2)  , (11.2.1)
, (11.2.1) , (11.3)
, (11.3)  , (11.3.1)
, (11.3.1) , (11.4)
, (11.4)  , (11.4.1)
, (11.4.1) ; (11.5)
; (11.5)  ; (11.5.1)
; (11.5.1) . (11.27)
. (11.27)Выборочные данные представлены в корреляционной таблице, где
 – количество пар
– количество пар  ,
,  ,
,  :
:
 – количество пар
– количество пар  ,
,  ,
,  :
:Пример. Проанализировано 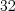 слова из фрагмента произведения С. Есенина :
слова из фрагмента произведения С. Есенина :  – количество букв в слове;
– количество букв в слове;  – количество согласных в слове. Получены следующие значения двумерной случайной величины
– количество согласных в слове. Получены следующие значения двумерной случайной величины 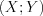 :
:
 ,
, 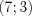 ,
, 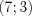 ,
,  ,
,  ,
, 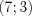 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Необходимо установить, существует ли зависимость между количеством гласных и количеством букв в слове.
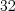 слова из фрагмента произведения С. Есенина :
слова из фрагмента произведения С. Есенина :  – количество букв в слове;
– количество букв в слове;  – количество согласных в слове. Получены следующие значения двумерной случайной величины
– количество согласных в слове. Получены следующие значения двумерной случайной величины 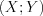 :
:  ,
, 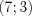 ,
, 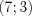 ,
,  ,
,  ,
, 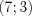 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. Необходимо установить, существует ли зависимость между количеством гласных и количеством букв в слове.
Решение. Построим интервальные вариационные ряды:
Заполним корреляционную таблицу (в качестве значений признаков взяты середины интервалов):
Ответ: Так как коэффициент корреляции равен  , то существует сильная статистическая зависимость между количеством гласных и количеством букв в слове.
, то существует сильная статистическая зависимость между количеством гласных и количеством букв в слове.
 , то существует сильная статистическая зависимость между количеством гласных и количеством букв в слове.
, то существует сильная статистическая зависимость между количеством гласных и количеством букв в слове.Коэффициентом корреляции двух случайных величин  и
и  называют число, которое находят по формуле:
называют число, которое находят по формуле:
 и
и  называют число, которое находят по формуле:
называют число, которое находят по формуле: .
.Свойства коэффициента корреляции:
1)  ;
;
 ;
;2) если случайные величины  и
и  независимы, то
независимы, то  ;
;
 и
и  независимы, то
независимы, то  ;
;3) если случайные величины  и
и  связаны линейной зависимостью, т. е.
связаны линейной зависимостью, т. е.  , то
, то  .
.
 и
и  связаны линейной зависимостью, т. е.
связаны линейной зависимостью, т. е.  , то
, то  .
.










