Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты

 , (10.18)
, (10.18)  , (10.18.1)
, (10.18.1)
 , где
, где 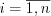 . (10.25)
. (10.25) , (10.27)
, (10.27) , (10.28)
, (10.28) , где
, где 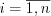 . (10.29)
. (10.29) . (10.31)
. (10.31)


 .
.
Ответ: .
.



 .
.
 .
.  .
. .
.
 ; (10.40)
; (10.40) . (10.41)
. (10.41)
Понятие случайной величины
Случайная величина – это величина, значения которой зависят от случая.
Н а п р и м е р, вес пойманной рыбы, температура воздуха в течение суток, сумма выигрыша лотерейного билета и т. п.
Случайная величина обозначается буквами  ,
,  ,
, 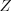 и т. д.
и т. д.
 ,
,  ,
, 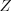 и т. д.
и т. д. Дискретная  принимает конечное или счетное множество значений;
принимает конечное или счетное множество значений;
 принимает конечное или счетное множество значений;
принимает конечное или счетное множество значений;Говорят, что задан закон распределения случайной величины  , если каждому значению
, если каждому значению  поставлена в соответствие вероятность его появления и сумма всех вероятностей равна числу
поставлена в соответствие вероятность его появления и сумма всех вероятностей равна числу  .
.
 , если каждому значению
, если каждому значению  поставлена в соответствие вероятность его появления и сумма всех вероятностей равна числу
поставлена в соответствие вероятность его появления и сумма всех вероятностей равна числу  .
. Закон распределения  может быть задан аналитически (формулой) или таблицей.
может быть задан аналитически (формулой) или таблицей.
 может быть задан аналитически (формулой) или таблицей.
может быть задан аналитически (формулой) или таблицей.Приведем табличный закон распределения дискретной  :
:
 :
:Функция распределения
Функция распределения дискретной  имеет вид:
имеет вид:
 имеет вид:
имеет вид: , (10.18)
, (10.18)где  означает, что суммируются вероятности тех значений, которые меньше
означает, что суммируются вероятности тех значений, которые меньше  , или иначе
, или иначе
 означает, что суммируются вероятности тех значений, которые меньше
означает, что суммируются вероятности тех значений, которые меньше  , или иначе
, или иначе , (10.18.1)
, (10.18.1)Н а п р и м е р, на рисунке 10.3 изображен график функции распределения некоторой дискретной случайной величины.

Вероятность того, что дискретная  примет значение из промежутка
примет значение из промежутка  равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.
равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.
 примет значение из промежутка
примет значение из промежутка  равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.
равна сумме вероятностей всех ее значений, принадлежащих данному промежутку.Числовые характеристики
1. Математическое ожидание  – это среднее значение величины
– это среднее значение величины  или центр ее распределения.
или центр ее распределения.
 – это среднее значение величины
– это среднее значение величины  или центр ее распределения.
или центр ее распределения.Математическое ожидание дискретной  , находят по формуле:
, находят по формуле:
 , находят по формуле:
, находят по формуле:  , где
, где 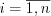 . (10.25)
. (10.25)Свойства математического ожидания
1. Математическое ожидание  заключено между ее наибольшим и наименьшим значениями.
заключено между ее наибольшим и наименьшим значениями.
 заключено между ее наибольшим и наименьшим значениями.
заключено между ее наибольшим и наименьшим значениями.2.  , где
, где  – константа.
– константа.
 , где
, где  – константа.
– константа.3.  , где
, где  – постоянный множитель.
– постоянный множитель.
 , где
, где  – постоянный множитель.
– постоянный множитель.4.  .
.
 .
.5.  , если случайные величины
, если случайные величины  и
и  независимые.
независимые.
 , если случайные величины
, если случайные величины  и
и  независимые.
независимые.2. Дисперсия или рассеивание  – это математическое ожидание квадрата отклонения величины
– это математическое ожидание квадрата отклонения величины  от ее математического ожидания:
от ее математического ожидания:
 – это математическое ожидание квадрата отклонения величины
– это математическое ожидание квадрата отклонения величины  от ее математического ожидания:
от ее математического ожидания:  , (10.27)
, (10.27)Дисперсию дискретной  можно найти по формуле:
можно найти по формуле:
 можно найти по формуле:
можно найти по формуле: , (10.28)
, (10.28)где
 , где
, где 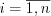 . (10.29)
. (10.29)Свойства дисперсии
1.  , где
, где  – константа.
– константа.
 , где
, где  – константа.
– константа.2.  , где
, где  – постоянный множитель.
– постоянный множитель.
 , где
, где  – постоянный множитель.
– постоянный множитель.3.  , если случайные величины
, если случайные величины  и
и  независимые.
независимые.
 , если случайные величины
, если случайные величины  и
и  независимые.
независимые.4.  , если случайные величины
, если случайные величины  и
и  независимые.
независимые.
 , если случайные величины
, если случайные величины  и
и  независимые.
независимые.3. Среднее квадратическое отклонение  – корень квадратный из ее дисперсии:
– корень квадратный из ее дисперсии:
 – корень квадратный из ее дисперсии:
– корень квадратный из ее дисперсии: . (10.31)
. (10.31)Пример 1. Распределение случайной величины  задано таблицей:
задано таблицей:
 задано таблицей:
задано таблицей:
Найдите вероятность того, что  примет значение, не большее чем
примет значение, не большее чем  .
.
 примет значение, не большее чем
примет значение, не большее чем  .
.Решение. Так как промежутку ![(-\infty ;3] LaTeX formula: (-\infty ;3]](/uploads/formulas/57a02752268007cd68f7643488a428dcf56f65eb.1.1.png) принадлежат два значения
принадлежат два значения  (
( и
и  ), то
), то
![(-\infty ;3] LaTeX formula: (-\infty ;3]](/uploads/formulas/57a02752268007cd68f7643488a428dcf56f65eb.1.1.png) принадлежат два значения
принадлежат два значения  (
( и
и  ), то
), то 
 .
. Ответ:
 .
.Пример 2. Постройте функцию распределения дискретной случайной величины  , заданной таблицей:
, заданной таблицей:
 , заданной таблицей:
, заданной таблицей:

График функции 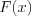 изображен на рисунке 10.5.
изображен на рисунке 10.5.
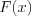 изображен на рисунке 10.5.
изображен на рисунке 10.5.
Пример 3. Распределение случайной величины  задано таблицей:
задано таблицей:
 задано таблицей:
задано таблицей:
Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение  .
.
 .
.  .
.
 .
.  .
. .
. Ответ: 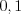 ;
;  ;
;  .
.
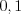 ;
;  ;
;  .
.1. Функция распределения дискретной  является разрывной.
является разрывной.
 является разрывной.
является разрывной.2. Математическое ожидание и дисперсия  являются частными случаями таких числовых характеристик как моменты случайных величин:
являются частными случаями таких числовых характеристик как моменты случайных величин:
 являются частными случаями таких числовых характеристик как моменты случайных величин:
являются частными случаями таких числовых характеристик как моменты случайных величин:начальный момент  -ой степени
-ой степени  находят по формуле:
находят по формуле:
 -ой степени
-ой степени  находят по формуле:
находят по формуле:  ; (10.40)
; (10.40)центральный момент  -ой степени случайной величины
-ой степени случайной величины  находят по формуле:
находят по формуле:
 -ой степени случайной величины
-ой степени случайной величины  находят по формуле:
находят по формуле:  . (10.41)
. (10.41)Частные случаи:  ,
,  .
.
 ,
,  .
.3. Асимметрией называют число  , которое характеризует степень отклонения плотности вероятностей от симметричной.
, которое характеризует степень отклонения плотности вероятностей от симметричной.
 , которое характеризует степень отклонения плотности вероятностей от симметричной.
, которое характеризует степень отклонения плотности вероятностей от симметричной.4. Эксцессом называют число  , которое характеризует остроту пика максимума плотности вероятностей.
, которое характеризует остроту пика максимума плотности вероятностей.
 , которое характеризует остроту пика максимума плотности вероятностей.
, которое характеризует остроту пика максимума плотности вероятностей.
