Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (10.8)
. (10.8) . (10.9)
. (10.9) . (10.10)
. (10.10) . (10.11)
. (10.11) . (10.12)
. (10.12) , (10.13)
, (10.13) . (10.13.1)
. (10.13.1) , (10.14)
, (10.14) . (10.14.1)
. (10.14.1)

Условная вероятность
Условной вероятностью события  называют вероятность события
называют вероятность события  , при условии, что событие
, при условии, что событие  произошло, и записывают:
произошло, и записывают:
 или
или  .
.
 называют вероятность события
называют вероятность события  , при условии, что событие
, при условии, что событие  произошло, и записывают:
произошло, и записывают:  или
или  .
. Событие  не зависит от события
не зависит от события  , если
, если
 не зависит от события
не зависит от события  , если
, если  . (10.8)
. (10.8)Событие  не зависит от события
не зависит от события  , если
, если
 не зависит от события
не зависит от события  , если
, если  . (10.9)
. (10.9)Если выполняются равенства (10.8) и (10.9), то события  и
и  независимые.
независимые.
 и
и  независимые.
независимые. Сложение событий
Наступление хотя бы одного из событий  или
или  называют суммой событий и символически обозначают
называют суммой событий и символически обозначают  .
.
 или
или  называют суммой событий и символически обозначают
называют суммой событий и символически обозначают  .
. 1. Если если события  и
и  несовместные, то
несовместные, то
 и
и  несовместные, то
несовместные, то . (10.10)
. (10.10)2. Если события  и
и  совместные, то
совместные, то
 и
и  совместные, то
совместные, то . (10.11)
. (10.11)Умножение событий
Наступление двух событий  и
и  называют произведением событий и символически обозначают
называют произведением событий и символически обозначают  .
.
 и
и  называют произведением событий и символически обозначают
называют произведением событий и символически обозначают  .
. 1. Если события  и
и  независимые, то
независимые, то
 и
и  независимые, то
независимые, то . (10.12)
. (10.12)2. Если события  и
и  зависимые, то
зависимые, то
 и
и  зависимые, то
зависимые, то , (10.13)
, (10.13) . (10.13.1)
. (10.13.1)Соотношения между событиями
Рассмотрим два произвольных независимых события  ,
,  и противоположные им события
и противоположные им события 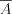 ,
,  .
.
Пусть ,
,  , а
, а  ,
,  .
.
 ,
,  и противоположные им события
и противоположные им события 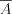 ,
,  .
. Пусть
 ,
,  , а
, а  ,
,  .
. Запись  означает, что хотя бы одно из двух событий произошло, а
означает, что хотя бы одно из двух событий произошло, а  .
.
 означает, что хотя бы одно из двух событий произошло, а
означает, что хотя бы одно из двух событий произошло, а  .
.Запись  означает, что хотя бы одно из двух событий не произошло, а
означает, что хотя бы одно из двух событий не произошло, а  .
.
 означает, что хотя бы одно из двух событий не произошло, а
означает, что хотя бы одно из двух событий не произошло, а  .
.Запись  означает, что оба события произошли, а
означает, что оба события произошли, а  .
.
 означает, что оба события произошли, а
означает, что оба события произошли, а  .
.Запись  означает, что ни одно событие не произошло, а
означает, что ни одно событие не произошло, а  .
.
 означает, что ни одно событие не произошло, а
означает, что ни одно событие не произошло, а  .
.Запись  означает, что событие
означает, что событие  произошло и не произошло событие
произошло и не произошло событие  , а
, а  .
.
 означает, что событие
означает, что событие  произошло и не произошло событие
произошло и не произошло событие  , а
, а  .
.Запись  означает, что произошло одно из событий, а
означает, что произошло одно из событий, а  .
.
 означает, что произошло одно из событий, а
означает, что произошло одно из событий, а  .
.Запись  означает, что произошло не более одного из событий, а
означает, что произошло не более одного из событий, а  .
.
 означает, что произошло не более одного из событий, а
означает, что произошло не более одного из событий, а  .
.Вероятность появления хотя бы одного события
1. Если события  ,
,  , …,
, …,  независимые, то вероятность появления хотя бы одного из этих событий можно найти по формуле:
независимые, то вероятность появления хотя бы одного из этих событий можно найти по формуле:
 ,
,  , …,
, …,  независимые, то вероятность появления хотя бы одного из этих событий можно найти по формуле:
независимые, то вероятность появления хотя бы одного из этих событий можно найти по формуле: , (10.14)
, (10.14)где  ,
,  , …,
, …,  .
.
 ,
,  , …,
, …,  .
.2. Если все события имеют одну и ту же вероятность  , то
, то 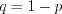 и
и
 , то
, то 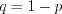 и
и  . (10.14.1)
. (10.14.1)Пример 1. Из урны, в которой имеется  синих и
синих и  красных шаров, наудачу берут шар и не возвращают обратно. Первым был вынут красный шар (событие
красных шаров, наудачу берут шар и не возвращают обратно. Первым был вынут красный шар (событие  ). Найдите вероятность того, что вторым вынут синий шар (событие
). Найдите вероятность того, что вторым вынут синий шар (событие  ).
).
 синих и
синих и  красных шаров, наудачу берут шар и не возвращают обратно. Первым был вынут красный шар (событие
красных шаров, наудачу берут шар и не возвращают обратно. Первым был вынут красный шар (событие  ). Найдите вероятность того, что вторым вынут синий шар (событие
). Найдите вероятность того, что вторым вынут синий шар (событие  ).
).Решение. Поскольку событие уже  произошло, то найдем условную вероятность события
произошло, то найдем условную вероятность события  .
.
Получим: .
.
Ответ: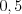 .
.
 произошло, то найдем условную вероятность события
произошло, то найдем условную вероятность события  .
. Получим:
 .
. Ответ:
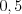 .
.Пример 2. Из урны, в которой имеется  белых и
белых и  красных шара, наудачу берут шар и не возвращают обратно. Найдите вероятность того, что первым был вынут белый шар (событие
красных шара, наудачу берут шар и не возвращают обратно. Найдите вероятность того, что первым был вынут белый шар (событие  ), а вторым красный шар (событие
), а вторым красный шар (событие  ).
).
 белых и
белых и  красных шара, наудачу берут шар и не возвращают обратно. Найдите вероятность того, что первым был вынут белый шар (событие
красных шара, наудачу берут шар и не возвращают обратно. Найдите вероятность того, что первым был вынут белый шар (событие  ), а вторым красный шар (событие
), а вторым красный шар (событие  ).
).Решение. В урне всего  шаров, следовательно,
шаров, следовательно,
 ,
,  .
.
 шаров, следовательно,
шаров, следовательно,  ,
,  .
. Ответ:  .
.
 .
.Пример 3. Вероятность получить на экзамене девять баллов (событие  ) у каждого из трех студентов равна
) у каждого из трех студентов равна 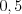 . Найдите вероятность того, что хотя бы один студент получит девять баллов.
. Найдите вероятность того, что хотя бы один студент получит девять баллов.
 ) у каждого из трех студентов равна
) у каждого из трех студентов равна 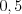 . Найдите вероятность того, что хотя бы один студент получит девять баллов.
. Найдите вероятность того, что хотя бы один студент получит девять баллов.Пример 4. В группе студентов, в которой  юношей и
юношей и  девушек, разыгрывается
девушек, разыгрывается  билетов в кино. Найдите вероятность того, что в кино пойдут три девушки.
билетов в кино. Найдите вероятность того, что в кино пойдут три девушки.
 юношей и
юношей и  девушек, разыгрывается
девушек, разыгрывается  билетов в кино. Найдите вероятность того, что в кино пойдут три девушки.
билетов в кино. Найдите вероятность того, что в кино пойдут три девушки. Решение. Применим урновую схему:

2)  ;
;
 ;
; 3)  .
.
 .
. Тогда,  .
.
 .
.Ответ:  .
.
 .
.Пример 5. Два стрелка независимо друг от друга производят по одному выстрелу по мишени. Вероятность поражения мишени первым стрелком равна  , а вторым –
, а вторым –  . Найдите вероятность того, что мишень будет поражена.
. Найдите вероятность того, что мишень будет поражена.
 , а вторым –
, а вторым –  . Найдите вероятность того, что мишень будет поражена.
. Найдите вероятность того, что мишень будет поражена.Решение. События  (попадание в мишень первым стрелком) и
(попадание в мишень первым стрелком) и  (вторым стрелком) совместные, так как не исключено одновременное попадание в мишень.
(вторым стрелком) совместные, так как не исключено одновременное попадание в мишень.
Следовательно, по формуле 10.11 получим:
 .
.
Ответ: .
.
 (попадание в мишень первым стрелком) и
(попадание в мишень первым стрелком) и  (вторым стрелком) совместные, так как не исключено одновременное попадание в мишень.
(вторым стрелком) совместные, так как не исключено одновременное попадание в мишень.Следовательно, по формуле 10.11 получим:
 .
. Ответ:
 .
.В случае, когда события  и
и  несовместные, то наряду с формулой
несовместные, то наряду с формулой  можно использовать и формулу
можно использовать и формулу  .
.
 и
и  несовместные, то наряду с формулой
несовместные, то наряду с формулой  можно использовать и формулу
можно использовать и формулу  .
. 



 , следовательно,
, следовательно,  .
. 


