Десятичной дробью называют дробь, у которой знаменателем являются
числа 
, 
, 
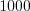и т. д.
Десятичные дроби
записывают так: пишут целую часть числа, ставят запятую и пишут его дробную
часть. Дробная часть числа должна содержать столько же цифр, сколько нулей
содержит знаменатель дроби.
Н а п р и м е р: 
; 
; 
.
Обращение десятичной
дроби в обыкновенную дробь
Чтобы обратить
десятичную дробь в обыкновенную, необходимо опустить запятую и записать
полученное число в числитель обыкновенной дроби, а в знаменатель этой дроби
записать цифру 
и столько нулей, сколько имелось цифр после запятой в
десятичной дроби.
Н а п р и м е р: 
; 
.
Свойства десятичных
дробей
1. Если в
десятичной дроби к последней цифре дробной части справа приписать любое
количество нулей, то получится равная ей дробь.
Н а п р и м е р: 
; 
.
2. Если в дробной части десятичной дроби
последняя цифра нуль (или несколько последних цифр нули), то получится равная
ей дробь, если последнюю цифру нуль (или несколько последних нулей) отбросить.
Н а п р и м е р: 
; 
.
3. Если перед первой цифрой в целой части
десятичной дроби слева приписать любое количество нулей, то получится равная ей
дробь.
Н а п р и м е р: 
; 
.
4. Любое натуральное число можно представить
десятичной дробью.
Н а п р и м е р: 
; 
.
Округление десятичных
дробей
При округлении
десятичных дробей до какого-нибудь разряда поступают так:
1) все цифры, следующие
за этим разрядом, заменяют нулями, если они стояли до запятой, или отбрасывают,
если они стояли после запятой;
2) последнюю оставшуюся
цифру не изменяют, если первая следующая за этим разрядом цифра 
, , 
, 
, 
;
3) последнюю оставшуюся цифру увеличивают на единицу, если первая следующая за этим
разрядом цифра 
, 
, 
, 
, 
.
Н а п р и м е р:
1) округлим число 
до десятков: 
;
2) округлим число 
до десятых: 
.
Сравнение десятичных
дробей
1. Чтобы сравнить десятичные дроби с разными
целыми частями, необходимо сравнить их целые части.
Н а п р и м е р: 
, так как 
.
2. Чтобы сравнить десятичные дроби с одинаковыми
целыми частями, необходимо уравнять число их знаков после запятой и сравнить
эти дроби поразрядно.
Н а п р и м е р: сравним
дроби 
и 
. Уравняем число знаков после запятых. Получим числа: 
и 
. Так как 
, то 
.
Правило сложения
десятичных дробей
Чтобы сложить десятичные
дроби столбиком, необходимо:
1) уравнять число знаков после запятых в слагаемых;
2) записать числа так,
чтобы запятая оказалась под запятой;
3) сложить дроби по
правилу сложения натуральных чисел;
3) в полученном числе
поставить запятую под запятыми слагаемых.
Правило вычитания
десятичных дробей
Чтобы вычесть десятичные
дроби столбиком, необходимо:
1) уравнять число знаков
после запятых в уменьшаемом и вычитаемом;
2) записать числа так,
чтобы запятая оказалась под запятой;
3) вычесть дроби по
правилу вычитания натуральных чисел;
3) в полученном числе
поставить запятую под запятыми уменьшаемого и вычитаемого.
Пример 1. Округлите число 
до: сотен,
единиц, десятых, сотых.
Решение.
1. Округляя число 
до сотен, цифры и заменяем нулями, цифры, стоящие после запятой,
отбрасываем, а цифру увеличим на единицу, так как первая из следующих за
разрядом сотен была цифра , и получим 
.
2. Округляя число до единиц, цифры, стоящие после
запятой, отбросим, цифру изменять не будем, так как первая из следующих за
разрядом единиц была цифра , и получим 
.
3. Округляя число до десятых, получим 
.
4. Округляя число до сотых, получим 
.
Пример 2. Найдите суммы чисел: 1) 
и 
; 2) 
и 
.
Решение.
Ответ: 
; 
.
Пример 3. Найдите разность чисел: 1) 
и 
; 2) 
и 
.
Решение.
Ответ: 
; 
.
Обращение обыкновенной
дроби в десятичную дробь
1. Любую обыкновенную дробь можно обратить в равную ей
десятичную дробь делением числителя на ее знаменатель.
Н а п р и м е р: 
; 
.
2. Если остатки отделения будут бесконечно повторяться, то
частное выразится бесконечной
периодической десятичной дробью. Группа повторяющихся цифр
образует период. Период принято
записывать в круглых скобках.
Н а п р и м е р: 
; 
.