Смешанными числами называют числа вида:  ,
,
где  – целая часть числа,
– целая часть числа, 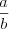 – его дробная часть.
– его дробная часть.
Преобразование обыкновенной дроби в смешанное число
Неправильную обыкновенную дробь (у которой числитель нацело не делится на знаменатель) можно представить в виде смешанного числа, если:
1) неполное частное числителя и знаменателя записать как целую часть смешанного числа;
2) остаток от деления записать в числитель дробной части;
3) знаменатель дроби оставить прежним.
Н а п р и м е р:  , так как
, так как  (ост.
(ост.  ).
).
Преобразование смешанного числа в обыкновенную дробь
Всякое смешанное число можно представить в виде обыкновенной дроби, если целую часть числа умножить на знаменатель дроби, затем к этому произведению прибавить числитель дроби и полученное число записать в числитель, а знаменатель оставить прежним: .
.
Н а п р и м е р:  .
.
Действия со смешанными числами
1. При сложении смешанных чисел, необходимо отдельно сложить их целые и дробные части.
Н а п р и м е р:  .
.
2. При вычитании смешанных чисел, необходимо:
1) из целой части уменьшаемого вычесть целую часть вычитаемого;
2) из дробной части уменьшаемого вычесть дробную часть вычитаемого;
3) полученные результаты сложить.
Н а п р и м е р:  .
.
Сравнение смешанных чисел
1. При сравнении смешанных чисел с разными целыми частями достаточно сравнить их целые части.
Н а п р и м е р: 1)  , так как
, так как  ; 2)
; 2)  , так как
, так как  .
.
2. При сравнении смешанных чисел с одинаковыми целыми частями необходимо сравнить их дробные части.
Н а п р и м е р: 1)  , так как
, так как  ; 2)
; 2)  , так как
, так как  .
.
Пример 1. Решите уравнение  .
.
Решение.
1.
Найдем неизвестное уменьшаемое:  ,
,  .
.
2.
Найдем неизвестное слагаемое:  ,
,  .
.
Ответ:  .
.
Пример 2. Укажите верные равенства:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение.
Преобразуем
смешанные числа в обыкновенные дроби:
1.
Равенство  верное, так как
верное, так как  .
.
2.
Равенство  верное, так как
верное, так как  и
и  .
.
3.
Равенство  неверное, так как
неверное, так как  .
.
Ответ:  ,
,  .
.
Пример 3. Укажите верные равенства:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение.
1.
Неверно, что  , так как
, так как  (ост.
(ост.  ).
).
2.
Неверно, что  , так как
, так как  .
.
3.
Верно, что  , так как
, так как  (ост.
(ост.  ).
).
Ответ:  .
.
Пример 4. Укажите верные неравенства:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение.
1.
Верно, что  , так как
, так как  и
и  .
.
2.
Верно, что  , так как
, так как  и
и 
(целые части равны, знаменатели дробных частей равны, числитель первой дроби больше числителя второй дроби).
3. Неверно, что  , так как
, так как  и
и 
(целые
части равны, числители дробных частей равны, а знаменатель первой дроби меньше
знаменателя второй дроби).
Ответ:  ;
;  .
.
1. Натуральное число (за исключением числа  ) можно всегда представить в виде смешанного числа.
) можно всегда представить в виде смешанного числа.
Например: 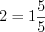 ,
,  .
.
2. У правильной обыкновенной дроби целая часть равна нулю.
3. У натурального числа дробная часть равна нулю.

