Деление натуральных чисел
Рассмотрим частное натуральных чисел  и
и  .
.
1. Если число  делится нацело на число
делится нацело на число  , то результатом деления будет натуральное число
, то результатом деления будет натуральное число  .
.
2. Если число  не делится нацело на число
не делится нацело на число  , то результат деления называют дробным числом и записывают в виде:
, то результат деления называют дробным числом и записывают в виде: 

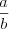 .
.
Обыкновенные дроби
Число вида 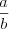
 и
и  – натуральные числа, называют обыкновенной дробью.
– натуральные числа, называют обыкновенной дробью.
Число  называется знаменателем дроби и показывает, на сколько равных частей разделена единица (целое).
называется знаменателем дроби и показывает, на сколько равных частей разделена единица (целое).
Число  называется числителем дроби и показывает, сколько таких частей взято.
называется числителем дроби и показывает, сколько таких частей взято.
Например, если  км разделить на
км разделить на  равных частей и пройти
равных частей и пройти  такие части пути, то пройденное расстояние составит две пятых километра:
такие части пути, то пройденное расстояние составит две пятых километра:  км.
км.
Правильные и неправильные дроби
1. Дробь 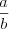 называется правильной, если ее числитель меньше знаменателя (
называется правильной, если ее числитель меньше знаменателя (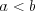 ).
).
2. Дробь 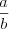 называется неправильной, если ее числитель не меньше знаменателя (
называется неправильной, если ее числитель не меньше знаменателя ( или
или  ).
).
Например, дроби  и
и  – правильные, а дроби
– правильные, а дроби  и
и  – неправильные.
– неправильные.
Правило нахождения дроби от числа
Чтобы найти дробь 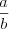 от числа
от числа  , необходимо число
, необходимо число  разделить на знаменатель дроби и результат умножить на числитель дроби:
разделить на знаменатель дроби и результат умножить на числитель дроби:  .
.
Например, найдем  от числа
от числа  . Получим:
. Получим:  .
.
Правило нахождения числа по его дроби
Чтобы найти число c по заданной величине  его дроби
его дроби 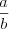 , необходимо разделить заданную величину
, необходимо разделить заданную величину  на числитель дроби и полученный результат умножить на знаменатель этой дроби:
на числитель дроби и полученный результат умножить на знаменатель этой дроби: .
.
Например, если  некоторого числа равны
некоторого числа равны  , то это число равно
, то это число равно  .
.
Пример 1. Даны дроби:  ,
,  ,
,  ,
,  . Найдите произведение знаменателей неправильных дробей.
. Найдите произведение знаменателей неправильных дробей.
Решение.
Дробь  правильная, так как
правильная, так как  .
.
Дробь  неправильная, так как
неправильная, так как  .
.
Дробь  неправильная, так как
неправильная, так как  .
.
Дробь  неправильная, так как
неправильная, так как  .
.
Найдем
произведение знаменателей неправильных дробей:  .
.
Ответ:  .
.
Пример 2. Туристы, отправляясь в
поход, запланировали пройти расстояние в  км
км  м. В первый
день они прошли
м. В первый
день они прошли  пути. Во второй день –
пути. Во второй день –  того, что прошли в
первый день, а в третий день
того, что прошли в
первый день, а в третий день  оставшегося пути. Какое
расстояние прошли туристы в третий день?
оставшегося пути. Какое
расстояние прошли туристы в третий день?
Решение.
1.
Найдем расстояние, которое прошли туристы в первый день:  (м).
(м).
2.
Найдем расстояние, которое прошли туристы во второй день:  (м).
(м).
3.
Найдем расстояние, которое туристы прошли за первые два дня: (м).
(м).
4.
Найдем расстояние, которое туристам осталось пройти:  (м).
(м).
5.
Найдем расстояние, которое туристы прошли в третий день:  (м).
(м).
Ответ:  км
км  м.
м.
Пример 3. Туристы отправились в
четырехдневный поход. В первый день они прошли  всего пути, что
составило
всего пути, что
составило  км, а во второй день –
км, а во второй день –  оставшегося пути.
Какое расстояние прошли туристы за два дня?
оставшегося пути.
Какое расстояние прошли туристы за два дня?
Решение.
1.
Найдем весь путь:  (км).
(км).
2.
Найдем оставшийся путь:  (км).
(км).
3.
Найдем расстояние, которое туристы прошли во второй день:  (км).
(км).
4.
Найдем расстояние, которое туристы прошли за первые два дня:  (км).
(км).
Ответ:  км.
км.
1. Любое натуральное число можно представить в виде обыкновенной дроби, знаменатель которой равен числу 1. Например:  ,
,  .
.
2. Число  можно представить в виде обыкновенной дроби, знаменатель которой равен любому натуральному числу. Например:
можно представить в виде обыкновенной дроби, знаменатель которой равен любому натуральному числу. Например:  ,
, 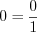 .
.
3. Число  всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю. Например:
всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю. Например: 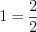 ,
,  .
.
Исключение составляет дробь  . Это выражение не имеет смысла.
. Это выражение не имеет смысла.

