Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты












Телом вращения называют пространственную фигуру, полученную в результате вращения некоторой плоской фигуры вокруг оси.
Среди всех тел вращения выделяют цилиндр, конус и шар.
Среди всех тел вращения выделяют цилиндр, конус и шар.
1. Цилиндр
Цилиндром называют фигуру, полученную в результате вращения прямоугольника вокруг одной из его сторон (оси цилиндра).
Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.
Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.
Н а п р и м е р, на рисунке 9.66 прямая – ось вращения;
– ось вращения;  – высота,
– высота,  – образующая цилиндра, полученного вращением прямоугольника
– образующая цилиндра, полученного вращением прямоугольника  вокруг стороны
вокруг стороны  . Основание цилиндра – круг радиуса
. Основание цилиндра – круг радиуса  . Прямоугольник
. Прямоугольник  – осевое сечение цилиндра.
– осевое сечение цилиндра.
Образующей цилиндра называют отрезок, соединяющий точки окружностей оснований цилиндра, и перпендикулярный диаметрам его оснований.
Высотой цилиндра называют перпендикуляр, заключенный между основаниями цилиндра.
Н а п р и м е р, на рисунке 9.66 прямая
 – ось вращения;
– ось вращения;  – высота,
– высота,  – образующая цилиндра, полученного вращением прямоугольника
– образующая цилиндра, полученного вращением прямоугольника  вокруг стороны
вокруг стороны  . Основание цилиндра – круг радиуса
. Основание цилиндра – круг радиуса  . Прямоугольник
. Прямоугольник  – осевое сечение цилиндра.
– осевое сечение цилиндра.Объем цилиндра высоты  находят по формуле:
находят по формуле:
 . (9.15)
. (9.15)
 находят по формуле:
находят по формуле:  . (9.15)
. (9.15)Площадь основания цилиндра ( – радиус основания) находят по формуле:
– радиус основания) находят по формуле:
 . (9.16)
. (9.16)
 – радиус основания) находят по формуле:
– радиус основания) находят по формуле:  . (9.16)
. (9.16)Площадь поверхности цилиндра находят по формуле:
 . (9.17)
. (9.17)
 . (9.17)
. (9.17)Площадь боковой поверхности цилиндра находят по формуле:
 , (9.18)
, (9.18)
где – радиус основания,
– радиус основания,  – высота,
– высота,  – образующая цилиндра.
– образующая цилиндра.
 , (9.18)
, (9.18) где
 – радиус основания,
– радиус основания,  – высота,
– высота,  – образующая цилиндра.
– образующая цилиндра.2. Конус
Конусом называют фигуру, полученную в результате вращения прямоугольного треугольника вокруг одного из катетов (оси конуса).
Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.
Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.
Н а п р и м е р, на рисунке 9.67 прямая – ось вращения;
– ось вращения;  – высота конуса,
– высота конуса,  – образующая конуса,
– образующая конуса,  – осевое сечение конуса, полученного вращением прямоугольного треугольника
– осевое сечение конуса, полученного вращением прямоугольного треугольника 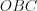 вокруг катета
вокруг катета  .
.
Образующей конуса называют отрезок, соединяющий вершину конуса с точкой окружности основания конуса.
Высотой конуса называют перпендикуляр, соединяющий вершину конуса с центром его основания.
Н а п р и м е р, на рисунке 9.67 прямая
 – ось вращения;
– ось вращения;  – высота конуса,
– высота конуса,  – образующая конуса,
– образующая конуса,  – осевое сечение конуса, полученного вращением прямоугольного треугольника
– осевое сечение конуса, полученного вращением прямоугольного треугольника 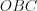 вокруг катета
вокруг катета  .
.Усеченным конусом называют часть конуса, ограниченную его основанием и сечением, параллельным плоскости основания.
Н а п р и м е р, на рисунке 9.68 изображен усеченный конус.
Н а п р и м е р, на рисунке 9.68 изображен усеченный конус.
Объем конуса высоты  находят по формуле:
находят по формуле:
 . (9.19)
. (9.19)
 находят по формуле:
находят по формуле:  . (9.19)
. (9.19)Площадь основания конуса ( – радиус основания) находят по формуле:
– радиус основания) находят по формуле:
 . (9.20)
. (9.20)
 – радиус основания) находят по формуле:
– радиус основания) находят по формуле:  . (9.20)
. (9.20)Площадь поверхности конуса находят по формуле:
 . (9.21)
. (9.21)
 . (9.21)
. (9.21)Площадь боковой поверхности конуса находят по формуле:
 , (9.22)
, (9.22)
где – радиус основания,
– радиус основания,  – образующая конуса.
– образующая конуса.
 , (9.22)
, (9.22) где
 – радиус основания,
– радиус основания,  – образующая конуса.
– образующая конуса.Объем усеченного конуса находят по формуле:
 , (9.23)
, (9.23)
где и
и  – радиусы оснований,
– радиусы оснований,  – высота.
– высота.
 , (9.23)
, (9.23) где
 и
и  – радиусы оснований,
– радиусы оснований,  – высота.
– высота.Площадь боковой поверхности усеченного конуса находят по формуле:
 , (9.24)
, (9.24)
где и
и  – радиусы оснований,
– радиусы оснований,  – высота,
– высота,  – образующая усеченного конуса.
– образующая усеченного конуса.
 , (9.24)
, (9.24) где
 и
и  – радиусы оснований,
– радиусы оснований,  – высота,
– высота,  – образующая усеченного конуса.
– образующая усеченного конуса.3. Шар и сфера
Сферой называют фигуру, полученную в результате вращения полуокружности вокруг ее диаметра (рис. 9.69).
Шаром называют фигуру, полученную вращением полукруга вокруг его диаметра.
Сечение сферы плоскостью – окружность. Сечение шара плоскостью – круг.
Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке и радиусом
и радиусом  ).
).
Сечение шара плоскостью, проходящей через центр шара, называют большим кругом (на рисунке 9.69 круг с центром в точке
 и радиусом
и радиусом  ).
). Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (на рисунке 9.69 плоскость  ).
).
Эту точку называют точкой касания сферы и плоскости (на рисунке 9.69 точка ).
).
Касательная плоскость перпендикулярна радиусу сферы в точке касания.
 ).
). Эту точку называют точкой касания сферы и плоскости (на рисунке 9.69 точка
 ).
). Касательная плоскость перпендикулярна радиусу сферы в точке касания.
Площадь сферы радиуса  находят по формуле:
находят по формуле:
 . (9.25)
. (9.25)
 находят по формуле:
находят по формуле:  . (9.25)
. (9.25)Объем шара радиуса находят по формуле:
находят по формуле:
 . (9.26)
. (9.26)
 находят по формуле:
находят по формуле:  . (9.26)
. (9.26)Выпуклый многоугольник вписан в сферу, если все его вершины лежат на поверхности сферы, и описан около сферы, если все его стороны касаются поверхности сферы.
Сферическим (шаровым) сегментом называют часть сферы (шара), отсекаемую плоскостью.
Высотой шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70
шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70  ).
).
Высотой
 шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70
шарового сегмента называют длину отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 9.70  ).
). Шаровым сектором называют тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов.
Высотой шарового сектора называют высоту части его сферической поверхности.
Н а п р и м е р, на рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса .
.
Высотой шарового сектора называют высоту части его сферической поверхности.
Н а п р и м е р, на рисунке 9.70 шаровой сектор получен в результате вращения кругового сектора вокруг радиуса
 .
.Объем шарового сегмента находят по формуле:
 . (9.27)
. (9.27)
 . (9.27)
. (9.27)Площадь сферической поверхности находят по формуле:
 , (9.28)
, (9.28)
где – радиус шара;
– радиус шара;  – высота сегмента.
– высота сегмента.
 , (9.28)
, (9.28) где
 – радиус шара;
– радиус шара;  – высота сегмента.
– высота сегмента.Объем шарового сектора находят по формуле:
 , (9.29)
, (9.29)
где – радиус шара;
– радиус шара;  – высота сегмента.
– высота сегмента.
 , (9.29)
, (9.29) где
 – радиус шара;
– радиус шара;  – высота сегмента.
– высота сегмента. Пример 1. Осевое сечение цилиндра – квадрат со стороной  . Найдите объем и площадь поверхности цилиндра.
. Найдите объем и площадь поверхности цилиндра.
 . Найдите объем и площадь поверхности цилиндра.
. Найдите объем и площадь поверхности цилиндра.
Решение. Так как осевое сечение квадрат (рис. 9.71), то  ,
,  .
.
По формулам 9.15 и 9.16 найдем объем цилиндра:
 .
.
По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра:
 .
.
Ответ: ;
;  .
.
 ,
,  .
. По формулам 9.15 и 9.16 найдем объем цилиндра:
 .
. По формулам 9.16 , 9.17 и 9.18 найдем площадь поверхности цилиндра:
 .
. Ответ:
 ;
;  .
.Пример 2. Площадь боковой поверхности цилиндра равна  , а объем его равен
, а объем его равен  . Найдите высоту этого цилиндра.
. Найдите высоту этого цилиндра.
 , а объем его равен
, а объем его равен  . Найдите высоту этого цилиндра.
. Найдите высоту этого цилиндра.Решение. Площадь боковой поверхности и объем цилиндра найдем по формулам 9.18 и 9.15 , где  – радиус основания,
– радиус основания,  – высота цилиндра.
– высота цилиндра.
Тогда согласно условию задачи запишем:
Разделим первое уравнение системы на второе и получим:
 ,
,  ,
,  .
.
 – радиус основания,
– радиус основания,  – высота цилиндра.
– высота цилиндра. Тогда согласно условию задачи запишем:

Разделим первое уравнение системы на второе и получим:
 ,
,  ,
,  .
. Найдем  из первого уравнения системы:
из первого уравнения системы:
 .
.
 из первого уравнения системы:
из первого уравнения системы:  .
. Ответ:  .
.
 .
. Пример 3. Найдите объем и площадь поверхности конуса, осевым сечением которого является правильный треугольник со стороной  см (рис. 9.72).
см (рис. 9.72).
 см (рис. 9.72).
см (рис. 9.72).
Решение. Так как  см, а
см, а  см, то из теоремы Пифагора:
см, то из теоремы Пифагора:
 ,
,  (см).
(см).
По формулам 9.19 и 9.20 найдем объем конуса:
 (
( ).
).
По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса:
 (
( ).
).
Ответ:
 ;
; 
 .
.
 см, а
см, а  см, то из теоремы Пифагора:
см, то из теоремы Пифагора:  ,
,  (см).
(см). По формулам 9.19 и 9.20 найдем объем конуса:
 (
( ).
). По формулам 9.20 , 9.21 и 9.22 найдем площадь поверхности конуса:
 (
( ).
). Ответ:

 ;
; 
 .
.Пример 4. Радиус основания конуса равен  , а угол при вершине в развертке его боковой поверхности равен
, а угол при вершине в развертке его боковой поверхности равен  . Определите объем конуса.
. Определите объем конуса.
 , а угол при вершине в развертке его боковой поверхности равен
, а угол при вершине в развертке его боковой поверхности равен  . Определите объем конуса.
. Определите объем конуса.
Решение. Рассмотрим конус радиуса  и развертку его боковой поверхности – круговой сектор радиуса
и развертку его боковой поверхности – круговой сектор радиуса  (рис. 9.73).
(рис. 9.73).
Найдем длину окружности в основании конуса:
 .
.
Найдем длину дуги в развертке боковой поверхности конуса:
 .
.
Так как , то
, то  и
и  .
.
Из теоремы Пифагора:
 ,
,  .
.
По формулам 9.19 и 9.20 найдем объем конуса:
 .
.
Ответ: .
.
 и развертку его боковой поверхности – круговой сектор радиуса
и развертку его боковой поверхности – круговой сектор радиуса  (рис. 9.73).
(рис. 9.73). Найдем длину окружности в основании конуса:
 .
. Найдем длину дуги в развертке боковой поверхности конуса:
 .
. Так как
 , то
, то  и
и  .
. Из теоремы Пифагора:
 ,
,  .
. По формулам 9.19 и 9.20 найдем объем конуса:
 .
. Ответ:
 .
.Пример 5. Осевое сечение конуса – равнобокая трапеция с основаниями  и
и  . Образующая конуса равна
. Образующая конуса равна  . Найдите площадь боковой поверхности и объем конуса.
. Найдите площадь боковой поверхности и объем конуса.
 и
и  . Образующая конуса равна
. Образующая конуса равна  . Найдите площадь боковой поверхности и объем конуса.
. Найдите площадь боковой поверхности и объем конуса. 
Решение. Имеем усеченный конус (рис. 9.74), радиусы оснований которого соответственно равны  и
и  .
.
Зная образующую конуса , найдем его высоту:
, найдем его высоту:
 ,
,  .
.
По формуле 9.24 найдем площадь боковой поверхности конуса:
 .
.
По формуле 9.23 найдем объем конуса:
 .
.
Ответ: ;
;  .
.
 и
и  .
. Зная образующую конуса
 , найдем его высоту:
, найдем его высоту:  ,
,  .
. По формуле 9.24 найдем площадь боковой поверхности конуса:
 .
. По формуле 9.23 найдем объем конуса:
 .
. Ответ:
 ;
;  .
.Пример 6. Периметр правильного шестиугольника, все вершины которого лежат на поверхности шара, равен  . Объем шара равен
. Объем шара равен  . Найдите расстояние от центра шара до плоскости шестиугольника.
. Найдите расстояние от центра шара до плоскости шестиугольника.
 . Объем шара равен
. Объем шара равен  . Найдите расстояние от центра шара до плоскости шестиугольника.
. Найдите расстояние от центра шара до плоскости шестиугольника. 
Решение. Найдем сторону правильного шестиугольника, зная его периметр:
 .
.
Так как радиус окружности, описанной около правильного шестиугольника, равен его стороне, то на рисунке 9.75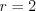 .
.
Объем шара находят по формуле 9.26 .
Так как , то
, то  ,
,  ,
,  ,
,  .
.
Из теоремы Пифагора:
 ,
,  .
.
Ответ: .
.
 .
. Так как радиус окружности, описанной около правильного шестиугольника, равен его стороне, то на рисунке 9.75
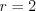 .
. Объем шара находят по формуле 9.26 .
Так как
 , то
, то  ,
,  ,
,  ,
,  .
. Из теоремы Пифагора:
 ,
,  .
. Ответ:
 .
.Пример 7. Сторона квадрата, описанного около шара, равна  . Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен
. Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен  (рис. 9.76).
(рис. 9.76).
 . Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен
. Найдите площадь сферической поверхности, отсекаемой плоскостью квадрата от шара, если радиус шара равен  (рис. 9.76).
(рис. 9.76).
Решение. 1. Найдем диагональ квадрата, зная его сторону:
 ,
,  .
.
Поскольку сечение шара плоскостью – круг, а квадрат описан около этого круга, то радиус сечения равен:
 ,
,  .
.
2. Из теоремы Пифагора:
 ,
,  .
.
3. Найдем высоту сферической поверхности:
 ,
,  .
.
4. По формуле 9.28 найдем площадь сферической поверхности:
 ,
,  .
.
Ответ: .
.
 ,
,  .
. Поскольку сечение шара плоскостью – круг, а квадрат описан около этого круга, то радиус сечения равен:
 ,
,  .
. 2. Из теоремы Пифагора:
 ,
,  .
. 3. Найдем высоту сферической поверхности:
 ,
,  .
. 4. По формуле 9.28 найдем площадь сферической поверхности:
 ,
,  .
. Ответ:
 .
. Пример 8. Равнобедренная трапеция с основаниями  см и
см и  см и острым углом
см и острым углом  вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.
вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.
 см и
см и  см и острым углом
см и острым углом  вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.
вращается вокруг меньшего основания. Вычислите поверхность полученной фигуры вращения.
Решение. Рассмотрим равнобедренную трапецию  с основаниями:
с основаниями:
 см и
см и  см (рис. 9.77).
см (рис. 9.77).
Вращая трапецию вокруг основания , получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов:
, получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов:
 .
.
В трапеции из вершин
из вершин  и
и  проведем высоты
проведем высоты  и
и  .
.
Тогда .
.
Рассмотрим прямоугольный треугольник :
:
 ,
,  (см),
(см),
 с основаниями:
с основаниями:  см и
см и  см (рис. 9.77).
см (рис. 9.77). Вращая трапецию вокруг основания
 , получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов:
, получим тело, боковая поверхность которого состоит из боковой поверхности цилиндра и боковой поверхности двух равных конусов:  .
. В трапеции
 из вершин
из вершин  и
и  проведем высоты
проведем высоты  и
и  .
. Тогда
 .
. Рассмотрим прямоугольный треугольник
 :
:  ,
,  (см),
(см), тогда  (см) и
(см) и  (см).
(см).
Согласно формуле получим:
получим:
 (
( ).
).
Согласно формуле получим:
получим:
 (
( ).
).
Найдем площадь поверхности тела вращения:
 (
( ).
).
Ответ:
 .
.
 (см) и
(см) и  (см).
(см). Согласно формуле
 получим:
получим: (
( ).
). Согласно формуле
 получим:
получим: (
( ).
). Найдем площадь поверхности тела вращения:
 (
( ).
). Ответ:

 .
.1. В цилиндре умейте определять: радиус основания, высоту, образующую, осевое сечение.
2. В конусе умейте определять: радиус основания, высоту, образующую, осевое сечение.
3. Различайте шар и сферу (поверхность шара).
Умейте определять:
1) центр, радиус и диаметр сферы;
2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.
Умейте определять:
1) центр, радиус и диаметр сферы;
2) в шаре: центр, радиус, диаметр, сечение, шаровой сегмент и шаровой сектор.

