Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты













Пирамидой называют многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной.
Многоугольник называют основанием пирамиды, а треугольники – боковыми гранями.
Высотой пирамиды называют перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания.
Н а п р и м е р, на рисунке 9.53 изображена четырехугольная пирамида с вершиной в точке
с вершиной в точке  . Четырехугольник
. Четырехугольник  – основание пирамиды, треугольники
– основание пирамиды, треугольники  ,
,  ,
,  и
и  – ее боковые грани. Отрезки
– ее боковые грани. Отрезки  ,
,  ,
,  и
и  – боковые ребра пирамиды. Отрезок
– боковые ребра пирамиды. Отрезок  – высота пирамиды.
– высота пирамиды.
Многоугольник называют основанием пирамиды, а треугольники – боковыми гранями.
Высотой пирамиды называют перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания.
Н а п р и м е р, на рисунке 9.53 изображена четырехугольная пирамида
 с вершиной в точке
с вершиной в точке  . Четырехугольник
. Четырехугольник  – основание пирамиды, треугольники
– основание пирамиды, треугольники  ,
,  ,
,  и
и  – ее боковые грани. Отрезки
– ее боковые грани. Отрезки  ,
,  ,
,  и
и  – боковые ребра пирамиды. Отрезок
– боковые ребра пирамиды. Отрезок  – высота пирамиды.
– высота пирамиды. 1. Если все боковые ребра пирамиды равны или наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, описанной около основания пирамиды.
2. Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом (двугранные углы при основании равны), то основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды.
3. Если две боковые грани пирамиды перпендикулярны плоскости основания, то боковое ребро, содержащее эти грани, является высотой пирамиды.
Объем пирамиды высоты  находят по формуле:
находят по формуле:
 , (9.11)
, (9.11)
 находят по формуле:
находят по формуле:  , (9.11)
, (9.11)Площадь поверхности пирамиды находят по формуле:
 . (9.12)
. (9.12)
 . (9.12)
. (9.12)Пирамида называется правильной, если ее основанием является правильный многоугольник, а основание высоты пирамиды, проведенной из ее вершины, совпадает с центром окружности, вписанной в основание пирамиды (или описанной около основания пирамиды, так как центры этих окружностей совпадают).
Н а п р и м е р, на рисунке 9.54 изображена правильная четырехугольная пирамида, а на рисунке 9.55 – правильная треугольная.
Н а п р и м е р, на рисунке 9.54 изображена правильная четырехугольная пирамида, а на рисунке 9.55 – правильная треугольная.
Высоту боковой грани правильной пирамиды, проведенную из ее вершины, называют апофемой.
Н а п р и м е р, на рисунке 9.54 отрезок – апофема правильной четырехугольной пирамиды.
– апофема правильной четырехугольной пирамиды.
Н а п р и м е р, на рисунке 9.54 отрезок
 – апофема правильной четырехугольной пирамиды.
– апофема правильной четырехугольной пирамиды. Любую треугольную пирамиду называют тетраэдром.
Тетраэдр называется правильным, если все его ребра равны.
Н а п р и м е р, на рисунке 9.56 изображен правильный тетраэдр.
Тетраэдр называется правильным, если все его ребра равны.
Н а п р и м е р, на рисунке 9.56 изображен правильный тетраэдр.
Площадь боковой поверхности правильной пирамиды находят по формуле:
 , (9.13)
, (9.13)
где – апофема пирамиды.
– апофема пирамиды.
 , (9.13)
, (9.13) где
 – апофема пирамиды.
– апофема пирамиды.Усеченной пирамидой называют многогранник, вершинами которого служат вершины основания пирамиды и вершины ее сечения плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники.
Высотой усеченной пирамиды называют перпендикуляр, заключенный между плоскостями ее оснований.
Н а п р и м е р, на рисунке 9.57 изображена треугольная усеченная пирамида, а на рисунке 9.58 – правильная четырехугольная усеченная пирамида.
Основания усеченной пирамиды – подобные многоугольники.
Высотой усеченной пирамиды называют перпендикуляр, заключенный между плоскостями ее оснований.
Н а п р и м е р, на рисунке 9.57 изображена треугольная усеченная пирамида, а на рисунке 9.58 – правильная четырехугольная усеченная пирамида.
Объем усеченной пирамиды находят по формуле:
 , (9.14)
, (9.14)
где и
и  – площади оснований,
– площади оснований,  – высота усеченной пирамиды.
– высота усеченной пирамиды.
 , (9.14)
, (9.14) где
 и
и  – площади оснований,
– площади оснований,  – высота усеченной пирамиды.
– высота усеченной пирамиды.Пример 1. Основанием пирамиды является правильный треугольник со стороной  дм, а две ее боковые грани перпендикулярны плоскости основания (рис. 9.59). Найдите объем пирамиды, зная, что ее высота равна
дм, а две ее боковые грани перпендикулярны плоскости основания (рис. 9.59). Найдите объем пирамиды, зная, что ее высота равна  дм.
дм.
 дм, а две ее боковые грани перпендикулярны плоскости основания (рис. 9.59). Найдите объем пирамиды, зная, что ее высота равна
дм, а две ее боковые грани перпендикулярны плоскости основания (рис. 9.59). Найдите объем пирамиды, зная, что ее высота равна  дм.
дм. 
Решение. Так как две боковые грани  и
и  пирамиды перпендикулярны плоскости ее основания, то их общее ребро
пирамиды перпендикулярны плоскости ее основания, то их общее ребро  является высотой пирамиды.
является высотой пирамиды.
Площадь основания пирамиды найдем по формуле:
 . Получим:
. Получим:  (
( ).
).
 и
и  пирамиды перпендикулярны плоскости ее основания, то их общее ребро
пирамиды перпендикулярны плоскости ее основания, то их общее ребро  является высотой пирамиды.
является высотой пирамиды. Площадь основания пирамиды найдем по формуле:
 . Получим:
. Получим:  (
( ).
). Пример 2. Вычислите объем правильного тетраэдра с ребром, равным  .
.
 .
.
Решение. Так как тетраэдр правильный (рис. 9.60), то его высота опускается в центр треугольника  : точку
: точку  , точку пересечения высот, биссектрис и медиан этого треугольника.
, точку пересечения высот, биссектрис и медиан этого треугольника.
Тогда – радиус окружности, описанной около
– радиус окружности, описанной около  ;
;  – высота тетраэдра.
– высота тетраэдра.
Найдем высоту тетраэдра. Рассмотрим треугольник .
.
Из теоремы Пифагора:
 ,
,  ,
,  .
.
Объем тетраэдра вычислим по формуле 9.11 , где .
.
Запишем: .
.
Ответ: .
.
 : точку
: точку  , точку пересечения высот, биссектрис и медиан этого треугольника.
, точку пересечения высот, биссектрис и медиан этого треугольника. Тогда
 – радиус окружности, описанной около
– радиус окружности, описанной около  ;
;  – высота тетраэдра.
– высота тетраэдра. Найдем высоту тетраэдра. Рассмотрим треугольник
 .
. Из теоремы Пифагора:
 ,
,  ,
,  .
. Объем тетраэдра вычислим по формуле 9.11 , где
 .
. Запишем:
 .
. Ответ:
 .
.Пример 3. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной  , и острым углом
, и острым углом  . Боковые ребра пирамиды наклонены к плоскости основания под углом
. Боковые ребра пирамиды наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
 , и острым углом
, и острым углом  . Боковые ребра пирамиды наклонены к плоскости основания под углом
. Боковые ребра пирамиды наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды. 
Решение. Основанием пирамиды является треугольник  :
:
 ;
;  (рис. 9.61).
(рис. 9.61).
Так как боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды опускается в центр окружности, описанной около этого треугольника (на рисунке 9.61 точка ).
).
Тогда и высота пирамиды
и высота пирамиды  .
.
 :
: ;
;  (рис. 9.61).
(рис. 9.61). Так как боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды опускается в центр окружности, описанной около этого треугольника (на рисунке 9.61 точка
 ).
).Тогда
 и высота пирамиды
и высота пирамиды  .
. Рассмотрим прямоугольный треугольник  .
.
Угол является углом наклона бокового ребра к плоскости основания, так как отрезок
является углом наклона бокового ребра к плоскости основания, так как отрезок  – проекция ребра
– проекция ребра  на плоскость основания и
на плоскость основания и  .
.
Тогда и
и  .
.
 .
. Угол
 является углом наклона бокового ребра к плоскости основания, так как отрезок
является углом наклона бокового ребра к плоскости основания, так как отрезок  – проекция ребра
– проекция ребра  на плоскость основания и
на плоскость основания и  .
. Тогда
 и
и  .
. Рассмотрим прямоугольный треугольник  :
:
 по свойству катета, лежащего против угла
по свойству катета, лежащего против угла  ;
;  .
.
 :
: по свойству катета, лежащего против угла
по свойству катета, лежащего против угла  ;
;  .
. Найдем площадь треугольника:
 ,
,  ,
,  .
.
 ,
,  ,
,  .
. Ответ:  .
.
 .
.Пример 4. Основанием пирамиды служит треугольник со сторонами  см,
см,  см и
см и  см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по
см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по 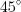 . Определите объем пирамиды.
. Определите объем пирамиды.
 см,
см,  см и
см и  см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по
см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по 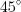 . Определите объем пирамиды.
. Определите объем пирамиды.
Решение. Основанием пирамиды (рис. 9.62) служит равнобедренный треугольник  :
:
 см,
см,  см.
см.
Так как боковые грани образуют с плоскостью основания равные двугранные углы, то высота пирамиды опускается в центр окружности, вписанной в треугольник , то есть в точку
, то есть в точку  , лежащую на высоте
, лежащую на высоте  этого треугольника.
этого треугольника.
 :
: см,
см,  см.
см. Так как боковые грани образуют с плоскостью основания равные двугранные углы, то высота пирамиды опускается в центр окружности, вписанной в треугольник
 , то есть в точку
, то есть в точку  , лежащую на высоте
, лежащую на высоте  этого треугольника.
этого треугольника. Тогда  см;
см;  , где
, где  – радиус окружности, вписанной в основание пирамиды и
– радиус окружности, вписанной в основание пирамиды и  .
.
 см;
см;  , где
, где  – радиус окружности, вписанной в основание пирамиды и
– радиус окружности, вписанной в основание пирамиды и  .
.Площадь треугольника  найдем по формуле Герона^
найдем по формуле Герона^
 , где
, где  (см) и
(см) и  (
( ).
).
 найдем по формуле Герона^
найдем по формуле Герона^  , где
, где  (см) и
(см) и  (
( ).
). Следовательно,  (см).
(см).
 (см).
(см).Угол  – линейный угол двугранного угла
– линейный угол двугранного угла  , так как
, так как  и
и  , и согласно условию задачи
, и согласно условию задачи  .
.
Значит, треугольник равнобедренный и
равнобедренный и  (см).
(см).
 – линейный угол двугранного угла
– линейный угол двугранного угла  , так как
, так как  и
и  , и согласно условию задачи
, и согласно условию задачи  .
. Значит, треугольник
 равнобедренный и
равнобедренный и  (см).
(см).Ответ: 
 .
.

 .
.Пример 5. Апофема правильной четырехугольной пирамиды (рис. 9.63) равна  и образует с высотой пирамиды угол
и образует с высотой пирамиды угол  . Найдите площадь боковой поверхности пирамиды.
. Найдите площадь боковой поверхности пирамиды.
 и образует с высотой пирамиды угол
и образует с высотой пирамиды угол  . Найдите площадь боковой поверхности пирамиды.
. Найдите площадь боковой поверхности пирамиды. 
Решение. Так как пирамида правильная, то четырехугольник  – квадрат, а ее боковые грани – равнобедренные треугольники.
– квадрат, а ее боковые грани – равнобедренные треугольники.
Точка – центр окружности, вписанной в основание пирамиды, следовательно,
– центр окружности, вписанной в основание пирамиды, следовательно,  .
.
Поскольку , а
, а  , то
, то  , тогда
, тогда  .
.
По формуле 9.13 найдем площадь боковой поверхности пирамиды:
 .
.
Ответ: .
.
 – квадрат, а ее боковые грани – равнобедренные треугольники.
– квадрат, а ее боковые грани – равнобедренные треугольники. Точка
 – центр окружности, вписанной в основание пирамиды, следовательно,
– центр окружности, вписанной в основание пирамиды, следовательно,  .
. Поскольку
 , а
, а  , то
, то  , тогда
, тогда  .
. По формуле 9.13 найдем площадь боковой поверхности пирамиды:
 .
.Ответ:
 .
.Пример 6. Основание пирамиды – ромб с острым углом  и стороной, равной
и стороной, равной  . Найдите объем пирамиды, если известно, что ее вершина удалена от всех сторон основания на расстояние, равное
. Найдите объем пирамиды, если известно, что ее вершина удалена от всех сторон основания на расстояние, равное  .
.
 и стороной, равной
и стороной, равной  . Найдите объем пирамиды, если известно, что ее вершина удалена от всех сторон основания на расстояние, равное
. Найдите объем пирамиды, если известно, что ее вершина удалена от всех сторон основания на расстояние, равное  .
.
Решение. Так как вершина пирамиды равноудалена от всех сторон ромба, то основание высоты пирамиды (точка  ) совпадает с центром окружности, вписанной в ромб (рис. 9.64).
) совпадает с центром окружности, вписанной в ромб (рис. 9.64).
По формуле найдем площадь ромба:
найдем площадь ромба:  .
.
С другой стороны, площадь ромба можем найти и по формуле:
 , откуда
, откуда  ,
,  .Тогда
.Тогда  .
.
Из теоремы Пифагора:
 ,
,  .
.
 ) совпадает с центром окружности, вписанной в ромб (рис. 9.64).
) совпадает с центром окружности, вписанной в ромб (рис. 9.64). По формуле
 найдем площадь ромба:
найдем площадь ромба:  .
. С другой стороны, площадь ромба можем найти и по формуле:
 , откуда
, откуда  ,
,  .Тогда
.Тогда  .
. Из теоремы Пифагора:
 ,
,  .
. Ответ:  .
.
 .
.Пример 7. Боковое ребро правильной четырехугольной усеченной пирамиды наклонено к плоскости основания под углом 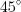 , а длины ребер оснований соответственно равны
, а длины ребер оснований соответственно равны  см и
см и  см (рис. 9.65). Найдите объем пирамиды.
см (рис. 9.65). Найдите объем пирамиды.
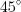 , а длины ребер оснований соответственно равны
, а длины ребер оснований соответственно равны  см и
см и  см (рис. 9.65). Найдите объем пирамиды.
см (рис. 9.65). Найдите объем пирамиды. 
Решение. Так как основания усеченной пирамиды – квадраты со сторонами  и
и  см, то их площади соответственно равны:
см, то их площади соответственно равны:

 ,
, 
 .
.
 и
и  см, то их площади соответственно равны:
см, то их площади соответственно равны: 
 ,
, 
 .
.По теореме Пифагора найдем диагонали квадратов:
 (см),
(см),
 (см).
(см).
 (см),
(см), (см).
(см).Так как диагонали точкой пересечения делятся пополам, то
 см, а
см, а  см.
см.
 см, а
см, а  см.
см. Рассмотрим диагональное сечение пирамиды – трапецию  .
.
Так как , то имеем прямоугольник
, то имеем прямоугольник  , в котором
, в котором  , а
, а  .
.
Поскольку треугольник равнобедренный, то
равнобедренный, то  (см) и
(см) и  см. Следовательно, высота усеченной пирамиды
см. Следовательно, высота усеченной пирамиды  см.
см.
 .
. Так как
 , то имеем прямоугольник
, то имеем прямоугольник  , в котором
, в котором  , а
, а  .
. Поскольку треугольник
 равнобедренный, то
равнобедренный, то  (см) и
(см) и  см. Следовательно, высота усеченной пирамиды
см. Следовательно, высота усеченной пирамиды  см.
см. Ответ: 
 .
.

 .
. 1. Решение задач, связанных с пирамидой, необходимо начинать с построения высоты пирамиды.
2. Различайте правильную треугольную пирамиду и правильный тетраэдр:
1) у правильной треугольной пирамиды основание – правильный треугольник, а боковые ребра хоть и равны между собой, но не обязательно, что они равны ребрам основания пирамиды;
2) правильный тетраэдр – это треугольная пирамида, у которой все ребра равны.








