Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты











Многогранник, две грани которого равные  -угольники, лежащие в параллельных плоскостях, а остальные
-угольники, лежащие в параллельных плоскостях, а остальные  граней – параллелограммы, называют
граней – параллелограммы, называют  -угольной призмой.
-угольной призмой.
 -угольники, лежащие в параллельных плоскостях, а остальные
-угольники, лежащие в параллельных плоскостях, а остальные  граней – параллелограммы, называют
граней – параллелограммы, называют  -угольной призмой.
-угольной призмой. Два  -угольника называют основаниями призмы, а параллелограммы – боковыми гранями.
-угольника называют основаниями призмы, а параллелограммы – боковыми гранями.
Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы.
Н а п р и м е р, на рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная.
 -угольника называют основаниями призмы, а параллелограммы – боковыми гранями.
-угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы.
Н а п р и м е р, на рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная.
Н а п р и м е р, на рисунке 9.42 треугольники и
и – основания призмы
– основания призмы , параллелограммы
, параллелограммы ,
, ,
, – боковые грани, отрезки
– боковые грани, отрезки ,
, ,
, – боковые ребра, отрезки
– боковые ребра, отрезки ,
,  ,
,  ,
,  ,
,  ,
,  – ребра оснований, точки
– ребра оснований, точки  ,
,  ,
,  ,
,  ,
,  ,
,  – вершины призмы.
– вершины призмы.
 и
и – основания призмы
– основания призмы , параллелограммы
, параллелограммы ,
, ,
, – боковые грани, отрезки
– боковые грани, отрезки ,
, ,
, – боковые ребра, отрезки
– боковые ребра, отрезки ,
,  ,
,  ,
,  ,
,  ,
,  – ребра оснований, точки
– ребра оснований, точки  ,
,  ,
,  ,
,  ,
,  ,
,  – вершины призмы.
– вершины призмы.Если грани призмы не имеют общего ребра, то их называют противоположными, если грани имеют общее ребро, то – смежными.
Н а п р и м е р, на рисунке 9.43 грани и
и  ,
,  и
и  , а также
, а также  и
и  являются противоположными, а, например, грани
являются противоположными, а, например, грани и
и  – смежными.
– смежными.
Н а п р и м е р, на рисунке 9.43 грани
 и
и  ,
,  и
и  , а также
, а также  и
и  являются противоположными, а, например, грани
являются противоположными, а, например, грани и
и  – смежными.
– смежными. Две вершины призмы, не принадлежащие одной грани, называют противоположными.
Н а п р и м е р, на рисунке 9.43 вершины и
и  – противоположные.
– противоположные.
Н а п р и м е р, на рисунке 9.43 вершины
 и
и  – противоположные.
– противоположные. Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ  на рисунке 9.41).
на рисунке 9.41).
 на рисунке 9.41).
на рисунке 9.41). Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.
Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.
Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43).
Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).
Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).
Высотой призмы называют перпендикуляр, заключенный между основаниями призмы.
Высота прямой призмы равна длине ее бокового ребра (рис. 9.42), высота
прямой призмы равна длине ее бокового ребра (рис. 9.42), высота  наклонной призмы – не равна (рис. 9.41 и 9.43).
наклонной призмы – не равна (рис. 9.41 и 9.43).
Высота
 прямой призмы равна длине ее бокового ребра (рис. 9.42), высота
прямой призмы равна длине ее бокового ребра (рис. 9.42), высота  наклонной призмы – не равна (рис. 9.41 и 9.43).
наклонной призмы – не равна (рис. 9.41 и 9.43).Диагональным сечением призмы называют сечение, содержащее диагональ призмы.
Н а п р и м е р, на рисунке 9.44 построены диагональные сечения и
и  четырехугольной призмы
четырехугольной призмы  .
.
Н а п р и м е р, на рисунке 9.44 построены диагональные сечения
 и
и  четырехугольной призмы
четырехугольной призмы  .
.Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44).
Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45).
Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник.
На рисунке 9.46 изображен прямоугольный параллелепипед.
На рисунке 9.46 изображен прямоугольный параллелепипед.
Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:
 , (9.1)
, (9.1)
где ,
,  ,
,  – длины ребер, выходящих из одной вершины,
– длины ребер, выходящих из одной вершины,  – диагональ параллелепипеда.
– диагональ параллелепипеда.
 , (9.1)
, (9.1) где
 ,
,  ,
,  – длины ребер, выходящих из одной вершины,
– длины ребер, выходящих из одной вершины,  – диагональ параллелепипеда.
– диагональ параллелепипеда. Объем прямоугольного параллелепипеда находят по формуле:
 . (9.2)
. (9.2)
 . (9.2)
. (9.2)Кубом называют прямоугольный параллелепипед с равными ребрами.
Все грани куба – квадраты (рис. 9.47).
Все грани куба – квадраты (рис. 9.47).
Объем куба с ребром  находят по формуле:
находят по формуле:
 . (9.3)
. (9.3)
 находят по формуле:
находят по формуле:  . (9.3)
. (9.3)Площадь поверхности куба с ребром  находят по формуле:
находят по формуле:
 . (9.4)
. (9.4)
 находят по формуле:
находят по формуле:  . (9.4)
. (9.4)Диагональ куба с ребром а находят по формуле:
 . (9.5)
. (9.5)
 . (9.5)
. (9.5)Объем прямой призмы высоты  и периметром основания
и периметром основания  находят по формуле:
находят по формуле:
 . (9.6)
. (9.6)
 и периметром основания
и периметром основания  находят по формуле:
находят по формуле:  . (9.6)
. (9.6)Площадь поверхности прямой призмы находят по формуле:
 . (9.7)
. (9.7)
 . (9.7)
. (9.7)Площадь боковой поверхности прямой призмы высоты  и периметром основания
и периметром основания  находят по формуле:
находят по формуле:
 . (9.8)
. (9.8)
 и периметром основания
и периметром основания  находят по формуле:
находят по формуле:  . (9.8)
. (9.8)Объем наклонной призмы можно вычислить по формуле:
 . (9.9)
. (9.9)
 . (9.9)
. (9.9) Площадь поверхности наклонной призмы можно вычислить по формулам:
 , (9.10)
, (9.10)
 , (9.9.1)
, (9.9.1)
 , (9.10.1)
, (9.10.1)
где сечение, перпендикулярное ребру
сечение, перпендикулярное ребру  (рис. 9.48).
(рис. 9.48).
 , (9.10)
, (9.10)  , (9.9.1)
, (9.9.1)  , (9.10.1)
, (9.10.1) где
 сечение, перпендикулярное ребру
сечение, перпендикулярное ребру  (рис. 9.48).
(рис. 9.48).Правильной призмой называют прямую призму, основанием которой является правильный многоугольник.
Пример 1. Найдите объем и площадь поверхности куба, зная, что его диагональ  см.
см.
 см.
см. Пример 2. Найдите объем прямоугольного параллелепипеда, диагональ которого равна  , а его измерения относятся как
, а его измерения относятся как  .
.
Решение. Согласно условию задачи запишем измерения параллелепипеда:
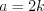 ,
, 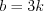 ,
,  .
.
 , а его измерения относятся как
, а его измерения относятся как  .
. Решение. Согласно условию задачи запишем измерения параллелепипеда:
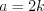 ,
, 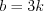 ,
,  .
.Пример 3. В основании прямой призмы лежит прямоугольный треугольник с катетами  см и
см и  см. Высота призмы равна
см. Высота призмы равна  см. Найдите площадь поверхности призмы.
см. Найдите площадь поверхности призмы.
 см и
см и  см. Высота призмы равна
см. Высота призмы равна  см. Найдите площадь поверхности призмы.
см. Найдите площадь поверхности призмы. Решение. 1. Площадь треугольника с катетами  и
и  найдем по формуле
найдем по формуле 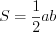 .
.
Получим: (
( ).
).
 и
и  найдем по формуле
найдем по формуле 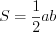 .
. Получим:
 (
( ).
).2. Гипотенузу  найдем по теореме Пифагора:
найдем по теореме Пифагора:
 (см).
(см).
 найдем по теореме Пифагора:
найдем по теореме Пифагора: (см).
(см).Ответ: 
 .
.

 .
. Пример 4. Объем наклонной треугольной призмы равен  , а боковое ребро
, а боковое ребро  . Правильный треугольник
. Правильный треугольник  – сечение, перпендикулярное боковому ребру
– сечение, перпендикулярное боковому ребру  (рис. 9.49). Найдите площадь боковой поверхности этой призмы.
(рис. 9.49). Найдите площадь боковой поверхности этой призмы.
 , а боковое ребро
, а боковое ребро  . Правильный треугольник
. Правильный треугольник  – сечение, перпендикулярное боковому ребру
– сечение, перпендикулярное боковому ребру  (рис. 9.49). Найдите площадь боковой поверхности этой призмы.
(рис. 9.49). Найдите площадь боковой поверхности этой призмы. 
2. Площадь правильного треугольника со стороной  находят по формуле
находят по формуле  .
.
Тогда ,
,  ,
, ![a=6\sqrt[4]{3} LaTeX formula: a=6\sqrt[4]{3}](/uploads/formulas/9062332f4d525b9d8d7d81f6f6b85e064e8a053a.1.1.png) .
.
 находят по формуле
находят по формуле  .
. Тогда
 ,
,  ,
, ![a=6\sqrt[4]{3} LaTeX formula: a=6\sqrt[4]{3}](/uploads/formulas/9062332f4d525b9d8d7d81f6f6b85e064e8a053a.1.1.png) .
. 3. Найдем периметр треугольника  :
:
![P=3a=18\sqrt[4]{3} LaTeX formula: P=3a=18\sqrt[4]{3}](/uploads/formulas/bbae5fd53c0113aaa76f374be2666d40fcfc8fe0.1.1.png) .
.
 :
: ![P=3a=18\sqrt[4]{3} LaTeX formula: P=3a=18\sqrt[4]{3}](/uploads/formulas/bbae5fd53c0113aaa76f374be2666d40fcfc8fe0.1.1.png) .
. Пример 5. Диагональ прямоугольного параллелепипеда равна  см, а диагонали его боковых граней равны
см, а диагонали его боковых граней равны  см и
см и  см. Определите объем параллелепипеда.
см. Определите объем параллелепипеда.
 см, а диагонали его боковых граней равны
см, а диагонали его боковых граней равны  см и
см и  см. Определите объем параллелепипеда.
см. Определите объем параллелепипеда.
Решение. Рассмотрим прямоугольный параллелепипед (рис. 9.50), где  ,
,  и
и  его измерения;
его измерения;  см – диагональ.
см – диагональ.
Согласно свойству 9.1 .
.
Рассмотрим треугольник . Так как
. Так как  см, то
см, то  .
.
Рассмотрим треугольник . Так как
. Так как  см, то
см, то  .
.
 ,
,  и
и  его измерения;
его измерения;  см – диагональ.
см – диагональ. Согласно свойству 9.1
 .
. Рассмотрим треугольник
 . Так как
. Так как  см, то
см, то  .
. Рассмотрим треугольник
 . Так как
. Так как  см, то
см, то  .
.Запишем и решим систему уравнений 

Из второго уравнения системы выразим  и получим:
и получим:  .
.
Из третьего уравнения выразим и получим:
и получим:  .
.
 и получим:
и получим:  .
. Из третьего уравнения выразим
 и получим:
и получим:  .
. Подставим полученные значения  и
и  в первое уравнение системы и найдем значение
в первое уравнение системы и найдем значение  :
:
 ,
,  ,
,  см.
см.
 и
и  в первое уравнение системы и найдем значение
в первое уравнение системы и найдем значение  :
:  ,
,  ,
,  см.
см.Зная  , определим значения
, определим значения  и
и  :
:
 ,
,  см;
см;
 ,
,  см.
см.
 , определим значения
, определим значения  и
и  :
:  ,
,  см;
см;  ,
,  см.
см.Ответ: 
 .
.

 .
. Пример 6. Найдите объем правильной шестиугольной призмы (рис. 9.52), зная, что большая диагональ призмы равна  и образует с плоскостью основания призмы угол
и образует с плоскостью основания призмы угол  .
.
 и образует с плоскостью основания призмы угол
и образует с плоскостью основания призмы угол  .
.
Решение. Рассмотрим большее диагональное сечение призмы  и прямоугольный треугольник
и прямоугольный треугольник 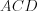 . Поскольку диагональ призмы
. Поскольку диагональ призмы  и образует с плоскостью основания угол
и образует с плоскостью основания угол  , то катет
, то катет  , лежащий против угла
, лежащий против угла  , равен половине гипотенузы, следовательно, высота призмы
, равен половине гипотенузы, следовательно, высота призмы  .
.
 и прямоугольный треугольник
и прямоугольный треугольник 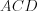 . Поскольку диагональ призмы
. Поскольку диагональ призмы  и образует с плоскостью основания угол
и образует с плоскостью основания угол  , то катет
, то катет  , лежащий против угла
, лежащий против угла  , равен половине гипотенузы, следовательно, высота призмы
, равен половине гипотенузы, следовательно, высота призмы  .
.Из теоремы Пифагора:
 ,
,  ,
,  .
.
 ,
,  ,
,  .
. Так как в основании призмы лежит правильный шестиугольник со стороной  , то
, то
 и
и  .
.
 , то
, то и
и  .
. По формуле  найдем площадь основания призмы:
найдем площадь основания призмы:  .
.
 найдем площадь основания призмы:
найдем площадь основания призмы:  .
. 1. Треугольная призма не имеет диагоналей.
2. Различайте прямую и наклонную призму: у наклонной призмы – боковые грани параллелограммы, у прямой призмы – боковые грани прямоугольники.
3. Если основание призмы – параллелограмм (ромб, прямоугольник, квадрат), то такую призму называют параллелепипедом. Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.




















 , откуда
, откуда  .
. ![S_{\delta.}=18\sqrt[4]{3} \cdot 10=180\sqrt[4]{3} LaTeX formula: S_{\delta.}=18\sqrt[4]{3} \cdot 10=180\sqrt[4]{3}](/uploads/formulas/4beb0a616447e168ffa829362dccc5b3c38a7d33.1.1.png)
![180\sqrt[4]{3} LaTeX formula: 180\sqrt[4]{3}](/uploads/formulas/33faac452da7bb4c66bf4747ea2479bc1160d0b4.1.1.png)


