Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты


 .
.
Десятичной дробью называют дробь, у которой знаменателем являются числа  ,
,  ,
, 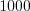 и т. д.
и т. д.
Это дробь вида , где
, где  – целое отличное от нуля число, а
– целое отличное от нуля число, а  – натуральное число.
– натуральное число.
Десятичные дроби принято записывать так: пишут целую часть числа, ставят запятую и пишут его дробную часть. При этом дробная часть должна содержать столько же цифр, сколько нулей содержит знаменатель дроби.
Н а п р и м е р: ;
;  .
.
 ,
,  ,
, 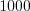 и т. д.
и т. д. Это дробь вида
 , где
, где  – целое отличное от нуля число, а
– целое отличное от нуля число, а  – натуральное число.
– натуральное число. Десятичные дроби принято записывать так: пишут целую часть числа, ставят запятую и пишут его дробную часть. При этом дробная часть должна содержать столько же цифр, сколько нулей содержит знаменатель дроби.
Н а п р и м е р:
 ;
;  .
.Свойства десятичных дробей
1. Если в десятичной дроби к последней цифре дробной части справа приписать любое количество нулей, то получится равная ей дробь.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
. 2. Если в дробной части десятичной дроби последняя цифра нуль (или несколько последних цифр нули), то получится равная ей дробь, если последнюю цифру нуль (или несколько последних нулей) отбросить.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
.3. Если перед первой цифрой в целой части десятичной дроби слева приписать любое количество нулей, то получится равная ей дробь.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
.4. Чтобы умножить десятичную дробь на  ,
,  ,
, 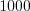 и т. д., необходимо запятую перенести на столько знаков вправо, сколько нулей записано после единицы у чисел
и т. д., необходимо запятую перенести на столько знаков вправо, сколько нулей записано после единицы у чисел  ,
,  ,
, 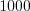 и т. д.
и т. д.
Н а п р и м е р: .
.
 ,
,  ,
, 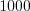 и т. д., необходимо запятую перенести на столько знаков вправо, сколько нулей записано после единицы у чисел
и т. д., необходимо запятую перенести на столько знаков вправо, сколько нулей записано после единицы у чисел  ,
,  ,
, 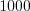 и т. д.
и т. д. Н а п р и м е р:
 .
.5. Чтобы разделить десятичную дробь на  ,
,  ,
, 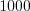 и т. д., необходимо запятую перенести на столько знаков влево, сколько нулей записано после единицы у чисел
и т. д., необходимо запятую перенести на столько знаков влево, сколько нулей записано после единицы у чисел  ,
,  ,
, 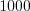 и т. д.
и т. д.
Н а п р и м е р, .
.
 ,
,  ,
, 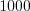 и т. д., необходимо запятую перенести на столько знаков влево, сколько нулей записано после единицы у чисел
и т. д., необходимо запятую перенести на столько знаков влево, сколько нулей записано после единицы у чисел  ,
,  ,
, 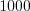 и т. д.
и т. д. Н а п р и м е р,
 .
.Правило сложения и вычитания десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, необходимо:
1) уравнять число знаков после запятых в слагаемых (уменьшаемом и вычитаемом);
2) записать числа так, чтобы запятая оказалась под запятой;
3) сложить (вычесть) дроби по правилу сложения (вычитания) натуральных чисел;
3) в полученном числе поставить запятую под запятыми слагаемых (уменьшаемого и вычитаемого).
Н а п р и м е р:
1) уравнять число знаков после запятых в слагаемых (уменьшаемом и вычитаемом);
2) записать числа так, чтобы запятая оказалась под запятой;
3) сложить (вычесть) дроби по правилу сложения (вычитания) натуральных чисел;
3) в полученном числе поставить запятую под запятыми слагаемых (уменьшаемого и вычитаемого).
Н а п р и м е р:

Правило умножения десятичных дробей
Чтобы умножить десятичные дроби, необходимо выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить справа столько цифр, сколько их содержится в обоих множителях вместе.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
. Правила деления десятичных дробей
1. При делении десятичной дроби на натуральное число запятую в частном ставят после того, как окончено деление целой части.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.2. При делении натурального числа или десятичной дроби на десятичную дробь в делимом и делителе переносят запятую вправо на столько цифр, сколько их содержится в делителе после запятой, и выполняют деление на натуральное число.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.Обращение обыкновенной дроби в десятичную дробь
Любую обыкновенную дробь можно обратить в равную ей десятичную дробь делением числителя на ее знаменатель.
1. Если в знаменателе несократимой дроби не имеется других простых делителей, кроме чисел и
и  , то частное выразится конечной десятичной дробью.
, то частное выразится конечной десятичной дробью.
Н а п р и м е р, .
.
1. Если в знаменателе несократимой дроби не имеется других простых делителей, кроме чисел
 и
и  , то частное выразится конечной десятичной дробью.
, то частное выразится конечной десятичной дробью. Н а п р и м е р,
 .
. 2. Если в знаменателе несократимой дроби имеются другие простые делители, а не только числа  и
и  , то остатки будут бесконечно повторяться, и частное выразится бесконечной периодической десятичной дробью. При этом группа повторяющихся цифр образует период. Период принято записывать в круглых скобках.
, то остатки будут бесконечно повторяться, и частное выразится бесконечной периодической десятичной дробью. При этом группа повторяющихся цифр образует период. Период принято записывать в круглых скобках.
Н а п р и м е р: .
.
 и
и  , то остатки будут бесконечно повторяться, и частное выразится бесконечной периодической десятичной дробью. При этом группа повторяющихся цифр образует период. Период принято записывать в круглых скобках.
, то остатки будут бесконечно повторяться, и частное выразится бесконечной периодической десятичной дробью. При этом группа повторяющихся цифр образует период. Период принято записывать в круглых скобках. Н а п р и м е р:
 .
.Обращение десятичной дроби в обыкновенную дробь
Любая конечная и любая бесконечная периодическая десятичная дробь может быть обращена в обыкновенную.
1. Чтобы обратить конечную десятичную дробь в обыкновенную, необходимо опустить запятую и записать полученное число в числитель обыкновенной дроби, а в знаменатель этой дроби записать цифру и столько нулей, сколько имелось цифр после запятой в десятичной дроби.
и столько нулей, сколько имелось цифр после запятой в десятичной дроби.
Н а п р и м е р: .
.
1. Чтобы обратить конечную десятичную дробь в обыкновенную, необходимо опустить запятую и записать полученное число в числитель обыкновенной дроби, а в знаменатель этой дроби записать цифру
 и столько нулей, сколько имелось цифр после запятой в десятичной дроби.
и столько нулей, сколько имелось цифр после запятой в десятичной дроби. Н а п р и м е р:
 .
.2. Чтобы обратить бесконечную десятичную периодическую дробь в обыкновенную, необходимо к числу, записанному до периода прибавить обыкновенную дробь, в числитель которой записать число, входящее в период, а в знаменатель записать цифру  столько раз, сколько цифр содержит период, и дописать столько нулей, сколько цифр между запятой и периодом.
столько раз, сколько цифр содержит период, и дописать столько нулей, сколько цифр между запятой и периодом.
Н а п р и м е р: .
.
 столько раз, сколько цифр содержит период, и дописать столько нулей, сколько цифр между запятой и периодом.
столько раз, сколько цифр содержит период, и дописать столько нулей, сколько цифр между запятой и периодом. Н а п р и м е р:
 .
.Округление десятичных дробей
При округлении десятичных дробей до какого-нибудь разряда поступают следующим образом:
1) все цифры, следующие за этим разрядом, заменяют нулями, если они стояли до запятой, или отбрасывают, если они стояли после запятой;
2) последнюю оставшуюся цифру не изменяют, если первая следующая за этим разрядом цифра  ,
,  ,
,  ,
,  ,
,  , или последнюю цифру увеличивают на единицу, если первая следующая за этим разрядом цифра
, или последнюю цифру увеличивают на единицу, если первая следующая за этим разрядом цифра  ,
,  ,
,  ,
,  или
или  .
.
 ,
,  ,
,  ,
,  ,
,  , или последнюю цифру увеличивают на единицу, если первая следующая за этим разрядом цифра
, или последнюю цифру увеличивают на единицу, если первая следующая за этим разрядом цифра  ,
,  ,
,  ,
,  или
или  .
. Сравнение десятичных дробей
1. Чтобы сравнить десятичные дроби с разными целыми частями, достаточно сравнить их целые части.
2. Чтобы сравнить десятичные дроби с одинаковыми целыми частями, необходимо уравнять число их знаков после запятой и сравнить эти дроби по правилам сравнения целых чисел и обыкновенных дробей.
Пример 1. Округлите число  до сотен, десятков, единиц, десятых и сотых.
до сотен, десятков, единиц, десятых и сотых.
 до сотен, десятков, единиц, десятых и сотых.
до сотен, десятков, единиц, десятых и сотых.Решение.
1. Округляя число до сотен, цифры
до сотен, цифры  и
и  заменим нулями, цифры, стоящие после запятой, отбросим, а цифру
заменим нулями, цифры, стоящие после запятой, отбросим, а цифру  изменять не будем, так как первая из следующих за разрядом сотен была цифра
изменять не будем, так как первая из следующих за разрядом сотен была цифра  , и получим
, и получим  .
.
1. Округляя число
 до сотен, цифры
до сотен, цифры  и
и  заменим нулями, цифры, стоящие после запятой, отбросим, а цифру
заменим нулями, цифры, стоящие после запятой, отбросим, а цифру  изменять не будем, так как первая из следующих за разрядом сотен была цифра
изменять не будем, так как первая из следующих за разрядом сотен была цифра  , и получим
, и получим  .
.2. Округляя число  до десятков, цифры, стоящие после запятой, отбросим, цифру
до десятков, цифры, стоящие после запятой, отбросим, цифру  заменим нулем, а цифру
заменим нулем, а цифру  увеличим на
увеличим на  , так как первая из следующих за разрядом десятков была цифра
, так как первая из следующих за разрядом десятков была цифра  , и получим
, и получим  .
.
 до десятков, цифры, стоящие после запятой, отбросим, цифру
до десятков, цифры, стоящие после запятой, отбросим, цифру  заменим нулем, а цифру
заменим нулем, а цифру  увеличим на
увеличим на  , так как первая из следующих за разрядом десятков была цифра
, так как первая из следующих за разрядом десятков была цифра  , и получим
, и получим  .
.3. Округляя число  до единиц, получим
до единиц, получим  .
.
 до единиц, получим
до единиц, получим  .
. 4. Округляя число  до десятых, получим
до десятых, получим  .
.
 до десятых, получим
до десятых, получим  .
. 5. Округляя число  до сотых, получим
до сотых, получим  .
.
 до сотых, получим
до сотых, получим  .
.Пример 2. Представьте в виде обыкновенной дроби числа  и
и  .
.
 и
и  .
.Решение.
 .
.
 .
.
 .
.Ответ:  ,
,  .
.
 ,
,  .
.1. Любое целое число можно представить десятичной дробью.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
. 2. Верно, что  , так как
, так как  .
.
 , так как
, так как  .
.
