Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты


























Простейшими фигурами в пространстве являются точка, прямая и плоскость.
Точки обозначают прописными буквами латинского алфавита: ,
,  ,
,  ,
, 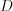 и т. д.
и т. д.
Прямые обозначают или строчными буквами латинского алфавита ,
,  ,
,  ,
,  или двумя прописными буквами
или двумя прописными буквами  ,
,  и т. д.
и т. д.
Плоскости обозначают строчными буквами греческого алфавита ,
,  ,
, 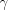 и т. д.
и т. д.
На рисунках плоскости изображают в виде произвольной области, а чаще в виде параллелограмма.
Н а п р и м е р, на рисунке 9.1 изображены плоскости ,
,  и
и 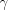 .
.
Точки обозначают прописными буквами латинского алфавита:
 ,
,  ,
,  ,
, 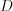 и т. д.
и т. д. Прямые обозначают или строчными буквами латинского алфавита
 ,
,  ,
,  ,
,  или двумя прописными буквами
или двумя прописными буквами  ,
,  и т. д.
и т. д. Плоскости обозначают строчными буквами греческого алфавита
 ,
,  ,
, 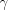 и т. д.
и т. д. На рисунках плоскости изображают в виде произвольной области, а чаще в виде параллелограмма.
Н а п р и м е р, на рисунке 9.1 изображены плоскости
 ,
,  и
и 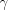 .
.Если точка  принадлежит плоскости
принадлежит плоскости  , то пишут:
, то пишут:  ; если точка
; если точка  не принадлежит этой плоскости, то пишут:
не принадлежит этой плоскости, то пишут:  (рис. 9.2).
(рис. 9.2).
 принадлежит плоскости
принадлежит плоскости  , то пишут:
, то пишут:  ; если точка
; если точка  не принадлежит этой плоскости, то пишут:
не принадлежит этой плоскости, то пишут:  (рис. 9.2).
(рис. 9.2). Если прямая с принадлежит плоскости  , то пишут:
, то пишут:  ; если прямая
; если прямая  не принадлежит этой плоскости, то пишут:
не принадлежит этой плоскости, то пишут:  (рис. 9.3).
(рис. 9.3).
 , то пишут:
, то пишут:  ; если прямая
; если прямая  не принадлежит этой плоскости, то пишут:
не принадлежит этой плоскости, то пишут:  (рис. 9.3).
(рис. 9.3).Аксиомы стереометрии
1. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Н а п р и м е р, на рисунке 9.4 через точки ,
,  и
и  проведена плоскость
проведена плоскость  .
.
Н а п р и м е р, на рисунке 9.4 через точки
 ,
,  и
и  проведена плоскость
проведена плоскость  .
.2. Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат данной плоскости.
Н а п р и м е р, на рисунке 9.5 точки и
и  прямой
прямой  принадлежат плоскости
принадлежат плоскости  , следовательно, прямая
, следовательно, прямая  принадлежит плоскости
принадлежит плоскости  .
.
Н а п р и м е р, на рисунке 9.5 точки
 и
и  прямой
прямой  принадлежат плоскости
принадлежат плоскости  , следовательно, прямая
, следовательно, прямая  принадлежит плоскости
принадлежит плоскости  .
.3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.
Н а п р и м е р, на рисунке 9.6 плоскости и
и 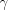 имеют общую точку
имеют общую точку  , принадлежащую прямой
, принадлежащую прямой  , следовательно, имеют общую прямую
, следовательно, имеют общую прямую  .
.
Н а п р и м е р, на рисунке 9.6 плоскости
 и
и 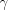 имеют общую точку
имеют общую точку  , принадлежащую прямой
, принадлежащую прямой  , следовательно, имеют общую прямую
, следовательно, имеют общую прямую  .
.Следствия из аксиом
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Н а п р и м е р, на рисунке 9.7 через прямую и точку
и точку проведена плоскость
проведена плоскость 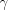 .
.
Н а п р и м е р, на рисунке 9.7 через прямую
 и точку
и точку проведена плоскость
проведена плоскость 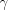 .
.2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Н а п р и м е р, на рисунке 9.8 через пересекающиеся прямые и
и  проведена плоскость
проведена плоскость  .
.
Н а п р и м е р, на рисунке 9.8 через пересекающиеся прямые
 и
и  проведена плоскость
проведена плоскость  .
.Взаимное расположение прямых в пространстве
Две прямые в пространстве могут быть параллельными, пересекаться ил скрещиваться.
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
Н а п р и м е р, на рисунке 9.9 прямые и
и  параллельны.
параллельны.
Н а п р и м е р, на рисунке 9.9 прямые
 и
и  параллельны.
параллельны. 2. Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.
Н а п р и м е р, на рисунке 9.10 прямые и
и  пересекаются под углом
пересекаются под углом  .
.
Н а п р и м е р, на рисунке 9.10 прямые
 и
и  пересекаются под углом
пересекаются под углом  .
. Две прямые называются перпендикулярными, если угол между ними прямой.
3. Две прямые в пространстве скрещиваются, если не существует плоскости, в которой они обе лежат.
Н а п р и м е р, на рисунке 9.11 изображены скрещивающиеся прямые и
и  .
.
Н а п р и м е р, на рисунке 9.11 изображены скрещивающиеся прямые
 и
и  .
. Признак скрещивающихся прямых: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Н а п р и м е р, на рисунке 9.12 прямая параллельна прямой
параллельна прямой  ,
,  – угол между скрещивающимися прямыми
– угол между скрещивающимися прямыми  и
и  .
.
Н а п р и м е р, на рисунке 9.12 прямая
 параллельна прямой
параллельна прямой  ,
,  – угол между скрещивающимися прямыми
– угол между скрещивающимися прямыми  и
и  .
.Взаимное расположение прямых и плоскостей
В пространстве прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости.
Н а п р и м е р, на рисунке 9.13 прямая пересекает плоскость
пересекает плоскость  в точке
в точке  .
.
На рисунке 9.14 прямая параллельна плоскости
параллельна плоскости  , а прямая
, а прямая  лежит в этой плоскости.
лежит в этой плоскости.
Н а п р и м е р, на рисунке 9.13 прямая
 пересекает плоскость
пересекает плоскость  в точке
в точке  .
. На рисунке 9.14 прямая
 параллельна плоскости
параллельна плоскости  , а прямая
, а прямая  лежит в этой плоскости.
лежит в этой плоскости.Плоскость и прямая, не принадлежащая плоскости, параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей этой плоскости, то она параллельна плоскости.
Н а п р и м е р, на рисунке 9.14 прямая принадлежит плоскости
принадлежит плоскости  , а прямая
, а прямая  параллельна прямой
параллельна прямой  и не принадлежит плоскости
и не принадлежит плоскости  , следовательно, прямая
, следовательно, прямая  параллельна плоскости
параллельна плоскости  .
.
Н а п р и м е р, на рисунке 9.14 прямая
 принадлежит плоскости
принадлежит плоскости  , а прямая
, а прямая  параллельна прямой
параллельна прямой  и не принадлежит плоскости
и не принадлежит плоскости  , следовательно, прямая
, следовательно, прямая  параллельна плоскости
параллельна плоскости  .
.Если плоскость содержит прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Н а п р и м е р, на рисунке 9.15 плоскость содержит прямую
содержит прямую  , параллельную плоскости
, параллельную плоскости  , и пересекает плоскость
, и пересекает плоскость  , следовательно, линия пересечения этих плоскостей
, следовательно, линия пересечения этих плоскостей  параллельна прямой
параллельна прямой  .
.
Н а п р и м е р, на рисунке 9.15 плоскость
 содержит прямую
содержит прямую  , параллельную плоскости
, параллельную плоскости  , и пересекает плоскость
, и пересекает плоскость  , следовательно, линия пересечения этих плоскостей
, следовательно, линия пересечения этих плоскостей  параллельна прямой
параллельна прямой  .
.Если через каждую из двух параллельных прямых проведены пересекающиеся плоскости, то линия их пересечения параллельна данным прямым.
Н а п р и м е р, на рисунке 9.16 через две параллельные прямые и
и  проведены пересекающиеся плоскости
проведены пересекающиеся плоскости  и
и  , следовательно, линия пересечения этих плоскостей
, следовательно, линия пересечения этих плоскостей  параллельна прямым
параллельна прямым  и
и  .
.
Н а п р и м е р, на рисунке 9.16 через две параллельные прямые
 и
и  проведены пересекающиеся плоскости
проведены пересекающиеся плоскости  и
и  , следовательно, линия пересечения этих плоскостей
, следовательно, линия пересечения этих плоскостей  параллельна прямым
параллельна прямым  и
и  .
.Взаимное расположение плоскостей в пространстве
Две плоскости в пространстве могут совпадать, быть параллельны или пересекаться.
Две плоскости параллельны, если они не имеют общих точек.
Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Н а п р и м е р, на рисунке 9.17 пересекающиеся прямые и
и  принадлежат плоскости
принадлежат плоскости  , а пересекающиеся прямые
, а пересекающиеся прямые  и
и  – плоскости
– плоскости  . При этом прямая
. При этом прямая  параллельна прямой
параллельна прямой  и прямая
и прямая  параллельна прямой
параллельна прямой  . Следовательно, данные плоскости параллельны.
. Следовательно, данные плоскости параллельны.
Н а п р и м е р, на рисунке 9.17 пересекающиеся прямые
 и
и  принадлежат плоскости
принадлежат плоскости  , а пересекающиеся прямые
, а пересекающиеся прямые  и
и  – плоскости
– плоскости  . При этом прямая
. При этом прямая  параллельна прямой
параллельна прямой  и прямая
и прямая  параллельна прямой
параллельна прямой  . Следовательно, данные плоскости параллельны.
. Следовательно, данные плоскости параллельны.Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости.
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Н а п р и м е р, на рисунке 9.18 прямая перпендикулярна каждой из двух пересекающихся прямых
перпендикулярна каждой из двух пересекающихся прямых  и
и  , принадлежащих плоскости
, принадлежащих плоскости  , следовательно, прямая
, следовательно, прямая  перпендикулярна данной плоскости.
перпендикулярна данной плоскости.
Н а п р и м е р, на рисунке 9.18 прямая
 перпендикулярна каждой из двух пересекающихся прямых
перпендикулярна каждой из двух пересекающихся прямых  и
и  , принадлежащих плоскости
, принадлежащих плоскости  , следовательно, прямая
, следовательно, прямая  перпендикулярна данной плоскости.
перпендикулярна данной плоскости.Свойства прямой, перпендикулярной плоскости
1. Два различных перпендикуляра к плоскости параллельны.
Н а п р и м е р, на рисунке 9.19 прямые и
и  перпендикулярны плоскости
перпендикулярны плоскости  , следовательно,
, следовательно,  .
.
Н а п р и м е р, на рисунке 9.19 прямые
 и
и  перпендикулярны плоскости
перпендикулярны плоскости  , следовательно,
, следовательно,  .
.2. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
Н а п р и м е р, на рисунке 9.20 плоскости и
и  параллельны. Прямая
параллельны. Прямая  перпендикулярна плоскости
перпендикулярна плоскости  , следовательно, она перпендикулярна и плоскости
, следовательно, она перпендикулярна и плоскости  .
.
Н а п р и м е р, на рисунке 9.20 плоскости
 и
и  параллельны. Прямая
параллельны. Прямая  перпендикулярна плоскости
перпендикулярна плоскости  , следовательно, она перпендикулярна и плоскости
, следовательно, она перпендикулярна и плоскости  .
.Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к плоскости.
Н а п р и м е р, на рисунке 9.21 прямая – наклонная к плоскости
– наклонная к плоскости  .
.
Н а п р и м е р, на рисунке 9.21 прямая
 – наклонная к плоскости
– наклонная к плоскости  .
.Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной к плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.
Н а п р и м е р, на рисунке 9.21 прямая – наклонная к плоскости, прямая
– наклонная к плоскости, прямая  – проекция этой наклонной на плоскость и
– проекция этой наклонной на плоскость и  . Тогда
. Тогда  .
.
Н а п р и м е р, на рисунке 9.21 прямая
 – наклонная к плоскости, прямая
– наклонная к плоскости, прямая  – проекция этой наклонной на плоскость и
– проекция этой наклонной на плоскость и  . Тогда
. Тогда  .
.Углом между прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Н а п р и м е р, на рисунке 9.22 прямая – наклонная к плоскости, прямая
– наклонная к плоскости, прямая  – проекция этой наклонной на плоскость, следовательно, угол
– проекция этой наклонной на плоскость, следовательно, угол  – угол между прямой
– угол между прямой  и плоскостью.
и плоскостью.
Н а п р и м е р, на рисунке 9.22 прямая
 – наклонная к плоскости, прямая
– наклонная к плоскости, прямая  – проекция этой наклонной на плоскость, следовательно, угол
– проекция этой наклонной на плоскость, следовательно, угол  – угол между прямой
– угол между прямой  и плоскостью.
и плоскостью.Двугранным углом называют угол, образованный двумя полуплоскостями с общей границей.
Прямую, которая является общей границей этих полуплоскостей, называют ребром двугранного угла, а полуплоскости с общим ребром – гранями двугранного угла.
Н а п р и м е р, на рисунке 9.23 изображен двугранный угол. Полуплоскости и
и  – грани этого угла, прямая
– грани этого угла, прямая  – ребро.
– ребро.
Прямую, которая является общей границей этих полуплоскостей, называют ребром двугранного угла, а полуплоскости с общим ребром – гранями двугранного угла.
Н а п р и м е р, на рисунке 9.23 изображен двугранный угол. Полуплоскости
 и
и  – грани этого угла, прямая
– грани этого угла, прямая  – ребро.
– ребро.В результате пересечения двух плоскостей образуется четыре двугранных угла (рис. 9.24).
Двугранный угол измеряется соответствующим линейным углом.
Линейным углом двугранного угла называют угол между перпендикулярами, проведенными в каждой грани к ребру.
Н а п р и м е р, на рисунке 9.25 угол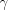 – линейный угол двугранного угла.
– линейный угол двугранного угла.
Двугранный угол измеряется соответствующим линейным углом.
Линейным углом двугранного угла называют угол между перпендикулярами, проведенными в каждой грани к ребру.
Н а п р и м е р, на рисунке 9.25 угол
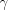 – линейный угол двугранного угла.
– линейный угол двугранного угла.Двугранный угол может иметь любое значение от  до
до  .
.
Если линейный угол двугранного угла равен , то плоскости перпендикулярны.
, то плоскости перпендикулярны.
 до
до  .
. Если линейный угол двугранного угла равен
 , то плоскости перпендикулярны.
, то плоскости перпендикулярны. Признак перпендикулярности плоскостей: если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.
Н а п р и м е р, на рисунке 9.26 плоскости и
и  перпендикулярны.
перпендикулярны.
Н а п р и м е р, на рисунке 9.26 плоскости
 и
и  перпендикулярны.
перпендикулярны.1. Плоскости в пространстве могут: совпадать; пересекаться (образуют двугранный угол); быть параллельными.
2. Прямые в пространстве могут: совпадать; пересекаться; быть параллельными; скрещиваться.
3. Прямая может: принадлежать плоскости; пересекать плоскость (ее называют наклонной к плоскости); быть ей параллельной.
4. Теорема о трех перпендикулярах устанавливает взаимосвязь между прямыми, пересекающими плоскость и прямыми, принадлежащими этой плоскости.

