Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты










 , (8.34)
, (8.34)  ; (8.35)
; (8.35) , (8.36)
, (8.36)  ; (8.37)
; (8.37) , (8.38)
, (8.38)  ; (8.39)
; (8.39) , (8.40)
, (8.40)  ; (8.41)
; (8.41) ; (8.42)
; (8.42) ; (8.43)
; (8.43) . (8.44)
. (8.44) , (8.45)
, (8.45)  . (8.46)
. (8.46)


 ,
,  .
. ,
,  ;
; ,
,  .
. .
.
 . (8.30)
. (8.30) . (8.32)
. (8.32)
Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).
Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).
Свойства вписанной окружности
1. Окружность можно вписать в любой треугольник.
2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.
Н а п р и м е р, на рисунке 8.106 .
.
Н а п р и м е р, на рисунке 8.106
 .
. Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.
Свойства описанной окружности
1. Окружность можно описать около любого треугольника.
2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.
Н а п р и м е р, на рисунке 8.107 .
.
Н а п р и м е р, на рисунке 8.107
 .
. Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
Расположение центров окружностей, описанных около треугольника:
1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;
2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);
б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);
3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);
4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).
Расположение центров окружностей, вписанных в треугольник:
1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);
2) центром окружности является точка пересечения биссектрис треугольника;
3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.
Формулы для вычисления радиусов вписанной и описанной окружностей
Радиус окружности, описанной около многоугольника, как правило, обозначают  , а радиус окружности, вписанной в многоугольник, обозначают
, а радиус окружности, вписанной в многоугольник, обозначают  :
:
 , а радиус окружности, вписанной в многоугольник, обозначают
, а радиус окружности, вписанной в многоугольник, обозначают  :
: 1) для равностороннего треугольника со стороной  :
:
 :
: , (8.34)
, (8.34)  ; (8.35)
; (8.35)2) для произвольного треугольника со сторонами  и площадью
и площадью  :
:
 и площадью
и площадью  :
:  , (8.36)
, (8.36)  ; (8.37)
; (8.37)3) для прямоугольного треугольника с катетами  и гипотенузой
и гипотенузой  :
:
 и гипотенузой
и гипотенузой  :
:  , (8.38)
, (8.38)  ; (8.39)
; (8.39)4) для квадрата со стороной  и диагональю
и диагональю  :
:
 и диагональю
и диагональю  :
:  , (8.40)
, (8.40)  ; (8.41)
; (8.41)5) для прямоугольника с диагональю  :
:
 :
:  ; (8.42)
; (8.42)6) для ромба с высотой  :
:
 :
:  ; (8.43)
; (8.43)7) для трапеции с высотой  , при условии, что в трапецию можно вписать окружность:
, при условии, что в трапецию можно вписать окружность:
 , при условии, что в трапецию можно вписать окружность:
, при условии, что в трапецию можно вписать окружность:  . (8.44)
. (8.44)Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами  и площадью
и площадью  , по формуле
, по формуле  найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
 и площадью
и площадью  , по формуле
, по формуле  найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);8) для правильного шестиугольника со стороной  :
:
 :
:  , (8.45)
, (8.45)  . (8.46)
. (8.46)Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка  является центром вписанной в него и описанной около него окружностей.
является центром вписанной в него и описанной около него окружностей.
 является центром вписанной в него и описанной около него окружностей.
является центром вписанной в него и описанной около него окружностей. Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна  .
.
 .
.Решение. Так как площадь круга радиуса  находят по формуле 8.32, а площадь квадрата со стороной
находят по формуле 8.32, а площадь квадрата со стороной  находят по формуле
находят по формуле  , то согласно условию задачи запишем:
, то согласно условию задачи запишем:
 ,
,  .
.
 находят по формуле 8.32, а площадь квадрата со стороной
находят по формуле 8.32, а площадь квадрата со стороной  находят по формуле
находят по формуле  , то согласно условию задачи запишем:
, то согласно условию задачи запишем: ,
,  .
.А так как  , то
, то
 ,
,  ,
,  ,
,  ,
,  .
.
Ответ: .
.
 , то
, то ,
,  ,
,  ,
,  ,
,  .
. Ответ:
 .
.Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами  и
и  находят по формуле
находят по формуле  .
.
Пусть , тогда
, тогда  (рис. 8.118).
(рис. 8.118).
Получим: ,
,  , откуда
, откуда  , следовательно,
, следовательно,  ,
,  .
.
 и
и  находят по формуле
находят по формуле  .
. Пусть
 , тогда
, тогда  (рис. 8.118).
(рис. 8.118). Получим:
 ,
,  , откуда
, откуда  , следовательно,
, следовательно,  ,
,  .
. Пример 3. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна  .
.
 .
.Решение. Площадь правильного треугольника со стороной  находят по формуле:
находят по формуле: 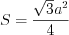 .
.
 находят по формуле:
находят по формуле: 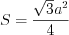 .
.Зная площадь треугольника, найдем его сторону:
 ,
,  ,
,  .
.
 ,
,  ,
,  .
. Пример 4. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.
Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой  находят по формуле 8.38. Тогда
находят по формуле 8.38. Тогда  .
.
 находят по формуле 8.38. Тогда
находят по формуле 8.38. Тогда  .
. Так как треугольник равнобедренный, то его катеты  и
и  раны и по теореме Пифагора
раны и по теореме Пифагора  , откуда
, откуда
 ,
,  .
.
 и
и  раны и по теореме Пифагора
раны и по теореме Пифагора  , откуда
, откуда  ,
,  .
. Пример 5. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).
Решение. Согласно свойству биссектрисы треугольника запишем:  , откуда
, откуда  .
.
 , откуда
, откуда  .
. Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.
В свою очередь по формуле Герона  найдем площадь треугольника.
найдем площадь треугольника.
 найдем площадь треугольника.
найдем площадь треугольника.Так как  , то
, то  .
.
 , то
, то  .
.Тогда  .
.
Ответ: .
.
 .
. Ответ:
 .
.Пример 6. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.
Решение. Согласно условию задачи и рисунку 8.122, запишем:
 ,
,  .
.
 ,
,  .
.По свойству четырехугольника, описанного около окружности, получим:
 ,
,  ,
,  .
.
 ,
,  ,
,  .
.Согласно формуле 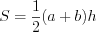 найдем площадь трапеции:
найдем площадь трапеции:
 .
.
Ответ: 45.
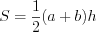 найдем площадь трапеции:
найдем площадь трапеции:  .
. Ответ: 45.
Пример 7. Длины оснований равнобедренной трапеции относятся как  , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.
, а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.
 , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.
, а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.Решение. Рассмотрим равнобедренную трапецию  (рис. 8.123) и проведем диагональ трапеции
(рис. 8.123) и проведем диагональ трапеции 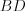 .
.
 (рис. 8.123) и проведем диагональ трапеции
(рис. 8.123) и проведем диагональ трапеции 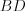 .
. ,
,  .
.Зная, что  и вводя коэффициент пропорциональности
и вводя коэффициент пропорциональности  , получим
, получим  ,
,  .
.
 и вводя коэффициент пропорциональности
и вводя коэффициент пропорциональности  , получим
, получим  ,
,  .
.Так как длина средней линии трапеции равна высоте трапеции, то
 , откуда
, откуда  . Тогда
. Тогда  ,
,  .
.
 , откуда
, откуда  . Тогда
. Тогда  ,
,  .
. Поскольку четырехугольник  является прямоугольником, то
является прямоугольником, то  , тогда
, тогда
 .
.
 является прямоугольником, то
является прямоугольником, то  , тогда
, тогда  .
.Согласно теореме Пифагора запишем:
 ,
,  ;
; ,
,  .
.По формуле 8.36 найдем радиус окружности, описанной около треугольника  , а, следовательно, и около трапеции
, а, следовательно, и около трапеции  :
:
 , а, следовательно, и около трапеции
, а, следовательно, и около трапеции  :
: .
.1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.
3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.
5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.
Длину окружности радиуса  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле:  . (8.30)
. (8.30)Площадь круга радиуса  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле:  . (8.32)
. (8.32)

 ,
, 






 .
. 




 .
.