Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты















 . (8.30)
. (8.30) . (8.31)
. (8.31) . (8.32)
. (8.32) . (8.33)
. (8.33)






Окружностью называют множество всех точек плоскости, равноудаленных от некоторой данной точки, называемой центром окружности.
Отрезок, соединяющий центр окружности и любую точку окружности, называют радиусом окружности.
Хордой называют отрезок, соединяющий две точки окружности.
Н а п р и м е р, на рисунке 8.83: точка – центр окружности; отрезки
– центр окружности; отрезки  и
и  – радиусы окружности; отрезки
– радиусы окружности; отрезки  и
и  – хорды окружности.
– хорды окружности.
Отрезок, соединяющий центр окружности и любую точку окружности, называют радиусом окружности.
Хордой называют отрезок, соединяющий две точки окружности.
Н а п р и м е р, на рисунке 8.83: точка
 – центр окружности; отрезки
– центр окружности; отрезки  и
и  – радиусы окружности; отрезки
– радиусы окружности; отрезки  и
и  – хорды окружности.
– хорды окружности. Если хорда перпендикулярна радиусу окружности, то точкой пересечения она делится пополам.
Н а п р и м е р, на рисунке 8.83 , следовательно,
, следовательно,  .
.
Н а п р и м е р, на рисунке 8.83
 , следовательно,
, следовательно,  .
.Хорду, проходящую через центр окружности, называют диаметром окружности.
Диаметр состоит из двух радиусов.
Н а п р и м е р, на рисунке 8.83 хорда – диаметр окружности и
– диаметр окружности и  .
.
Диаметр состоит из двух радиусов.
Н а п р и м е р, на рисунке 8.83 хорда
 – диаметр окружности и
– диаметр окружности и  .
. Дугой окружности называют часть окружности, заключенную между двумя точками окружности.
Если точки – концы диаметра окружности, то имеем две равные дуги, называемые полуокружностями.
Н а п р и м е р, на рисунке 8.84 изображены дуги окружности: и т.д. Среди них две равные полуокружности
и т.д. Среди них две равные полуокружности  .
.
Если точки – концы диаметра окружности, то имеем две равные дуги, называемые полуокружностями.
Н а п р и м е р, на рисунке 8.84 изображены дуги окружности:
 и т.д. Среди них две равные полуокружности
и т.д. Среди них две равные полуокружности  .
. Дуги можно измерять в угловых единицах. Градусная мера полуокружности равна  .
.
 .
.Кругом называют часть плоскости, ограниченную окружностью, включая точки окружности.
Н а п р и м е р, на рисунке 8.85 изображен круг.
Н а п р и м е р, на рисунке 8.85 изображен круг.
Круговым сектором называют часть круга, ограниченную радиусами и дугой, на которую опираются радиусы.
Н а п р и м е р, на рисунке 8.86 изображен круговой сектор .
.
Н а п р и м е р, на рисунке 8.86 изображен круговой сектор
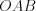 .
. Круговым сегментом называют часть круга, отсекаемую хордой.
Н а п р и м е р, на рисунке 8.87 изображен круговой сегмент .
.
Н а п р и м е р, на рисунке 8.87 изображен круговой сегмент
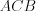 .
.Свойство пересекающихся хорд: если через точку, лежащую внутри окружности, проведены две хорды, то произведения отрезков, на которые хорды делятся в точке пересечения, равны.
Н а п р и м е р, на рисунке 8.88 .
.
Н а п р и м е р, на рисунке 8.88
 .
. Касательной к окружности называют прямую, имеющую с окружностью только одну общую точку.
Н а п р и м е р, на рисунке 8.89 из точки к окружности проведены касательные
к окружности проведены касательные  и
и 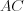 .
.
Н а п р и м е р, на рисунке 8.89 из точки
 к окружности проведены касательные
к окружности проведены касательные  и
и 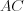 .
.Если к окружности из одной точки провести две касательные, то окружность будет вписана в угол, образованный этими касательными.
Центр окружности, вписанной в угол, расположен на биссектрисе угла (рис. 8.89).
Центр окружности, вписанной в угол, расположен на биссектрисе угла (рис. 8.89).
Свойства касательных
1. Отрезки касательных, проведенных из одной точки к окружности, равны (  на рис. 8.89).
на рис. 8.89).
 на рис. 8.89).
на рис. 8.89).2. Радиус окружности перпендикулярен касательной в точке касания (  на рис. 8.89).
на рис. 8.89).
 на рис. 8.89).
на рис. 8.89). Свойство хорды и касательной: угол, образованный хордой и касательной, проходящей через конец хорды, измеряется половиной дуги, заключенной внутри его.
Н а п р и м е р, на рисунке 8.90 – касательная к окружности,
– касательная к окружности, 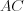 – хорда окружности,
– хорда окружности,
 и
и  .
.
Н а п р и м е р, на рисунке 8.90
 – касательная к окружности,
– касательная к окружности, 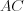 – хорда окружности,
– хорда окружности,  и
и  .
.Секущей называют прямую, имеющую с окружностью две общие точки.
Н а п р и м е р, на рисунке 8.91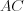 – отрезок секущей, а
– отрезок секущей, а  – внешняя часть отрезка секущей.
– внешняя часть отрезка секущей.
Н а п р и м е р, на рисунке 8.91
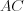 – отрезок секущей, а
– отрезок секущей, а  – внешняя часть отрезка секущей.
– внешняя часть отрезка секущей.Свойство касательной и секущей: если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной равен произведению отрезка секущей и ее внешней части.
Н а п р и м е р, на рисунке 8.91 .
.
Н а п р и м е р, на рисунке 8.91
 .
.Свойство секущих к окружности: если из одной точки к окружности проведены секущие, то все произведения отрезков секущих и их внешних частей равны.
Н а п р и м е р, на рисунке 8.92 .
.
Н а п р и м е р, на рисунке 8.92
 .
.Угол называют центральным, если его вершина лежит в центре окружности, а стороны являются радиусами окружности.
Центральный угол измеряется дугой, на которую он опирается.
Н а п р и м е р, на рисунке 8.93 изображен центральный угол .
.
Центральный угол измеряется дугой, на которую он опирается.
Н а п р и м е р, на рисунке 8.93 изображен центральный угол
 .
. Угол называют вписанным в окружность, если его вершина лежит на окружности, а стороны являются непересекающимися хордами этой окружности.
Н а п р и м е р, на рисунке 8.94 изображен вписанный в окружность угол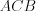 .
.
Н а п р и м е р, на рисунке 8.94 изображен вписанный в окружность угол
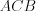 .
.Свойства вписанных в окружность углов
1. Вписанный в окружность угол равен половине соответствующего ему центрального угла.
Н а п р и м е р, на рисунке 8.95.
на рисунке 8.95.
Н а п р и м е р,
 на рисунке 8.95.
на рисунке 8.95.2. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 8.96).
3. Вписанные углы, опирающиеся на диаметр, прямые (рис. 8.97).
Длину окружности радиуса  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле:  . (8.30)
. (8.30)Длину дуги окружности радиуса  c центральным углом
c центральным углом  находят по формуле:
находят по формуле:
 c центральным углом
c центральным углом  находят по формуле:
находят по формуле:  . (8.31)
. (8.31)Площадь круга радиуса  находят по формуле:
находят по формуле:
 находят по формуле:
находят по формуле:  . (8.32)
. (8.32)Площадь кругового сектора радиуса  с центральным углом
с центральным углом  находят по формуле:
находят по формуле:
 с центральным углом
с центральным углом  находят по формуле:
находят по формуле:  . (8.33)
. (8.33)Пример 1. К окружности (рис. 8.98) проведены три касательные так, что в результате их пересечения образовался прямоугольный треугольник  . При этом отрезок
. При этом отрезок  см, а отрезок
см, а отрезок  см. Найдите катеты этого треугольника.
см. Найдите катеты этого треугольника.
 . При этом отрезок
. При этом отрезок  см, а отрезок
см, а отрезок  см. Найдите катеты этого треугольника.
см. Найдите катеты этого треугольника.
Решение. Так как отрезки касательных, проведенных из одной точки к окружности, равны, то:
 см,
см,  см.
см.
Пусть см, тогда
см, тогда  см,
см,  см,
см,  см.
см.
 см,
см,  см.
см. Пусть
 см, тогда
см, тогда  см,
см,  см,
см,  см.
см. Найдем катеты треугольника:
 (см),
(см),  (см).
(см).
Ответ: 6 см и 8 см.
 (см),
(см),  (см).
(см). Ответ: 6 см и 8 см.
Пример 2. В окружность вписан угол  , равный
, равный  . Хорды
. Хорды  и
и  соответственно равны 3 и
соответственно равны 3 и  . Найдите длину окружности.
. Найдите длину окружности.
 , равный
, равный  . Хорды
. Хорды  и
и  соответственно равны 3 и
соответственно равны 3 и  . Найдите длину окружности.
. Найдите длину окружности.
Так как угол  вписан в окружность, а угол
вписан в окружность, а угол  соответствующий ему центральный угол, то:
соответствующий ему центральный угол, то:
 и
и  .
.
Отрезки и
и  радиусы окружности.
радиусы окружности.
Следовательно, треугольник – равнобедренный и углы при его основании равны:
– равнобедренный и углы при его основании равны:
 .
.
Тогда треугольник – равносторонний и
– равносторонний и  .
.
Длину окружности найдем по формуле 8.30. Получим: .
.
Ответ: .
.
 вписан в окружность, а угол
вписан в окружность, а угол  соответствующий ему центральный угол, то:
соответствующий ему центральный угол, то: и
и  .
. Отрезки
 и
и  радиусы окружности.
радиусы окружности. Следовательно, треугольник
 – равнобедренный и углы при его основании равны:
– равнобедренный и углы при его основании равны:  .
. Тогда треугольник
 – равносторонний и
– равносторонний и  .
. Длину окружности найдем по формуле 8.30. Получим:
 .
. Ответ:
 .
. Пример 3. Прямой угол  вписан в окружность, радиус которой равен 9, а центральный угол
вписан в окружность, радиус которой равен 9, а центральный угол  равен
равен  . Найдите длину дуги
. Найдите длину дуги  (рис. 8.100).
(рис. 8.100).
 вписан в окружность, радиус которой равен 9, а центральный угол
вписан в окружность, радиус которой равен 9, а центральный угол  равен
равен  . Найдите длину дуги
. Найдите длину дуги  (рис. 8.100).
(рис. 8.100).
Решение. Так как  , то центральный угол
, то центральный угол  развернутый.
развернутый.
Так как углы и
и  смежные, то
смежные, то
 .
.
Длину дуги найдем по формуле 8.31:
найдем по формуле 8.31:
 .
.
Ответ: .
.
 , то центральный угол
, то центральный угол  развернутый.
развернутый. Так как углы
 и
и  смежные, то
смежные, то .
. Длину дуги
 найдем по формуле 8.31:
найдем по формуле 8.31: .
. Ответ:
 .
. Пример 4. Площадь кругового сектора с центральным углом  равна
равна  . Найдите длину дуги, ограничивающей этот сектор.
. Найдите длину дуги, ограничивающей этот сектор.
 равна
равна  . Найдите длину дуги, ограничивающей этот сектор.
. Найдите длину дуги, ограничивающей этот сектор.Пример 5. Из внешней точки к окружности проведены касательная и секущая. Длина касательной составляет  внутреннего отрезка секущей. Определите длину секущей, если длина касательной равна 6 см.
внутреннего отрезка секущей. Определите длину секущей, если длина касательной равна 6 см.
 внутреннего отрезка секущей. Определите длину секущей, если длина касательной равна 6 см.
внутреннего отрезка секущей. Определите длину секущей, если длина касательной равна 6 см.
Решение. Отметим вне окружности точку  и проведем из этой точки к окружности секущую
и проведем из этой точки к окружности секущую  и касательную
и касательную  (рис. 8.101).
(рис. 8.101).
Определим внутренний отрезок секущей:
 см.
см.
Пусть внешний отрезок касательной см.
см.
 и проведем из этой точки к окружности секущую
и проведем из этой точки к окружности секущую  и касательную
и касательную  (рис. 8.101).
(рис. 8.101). Определим внутренний отрезок секущей:
 см.
см. Пусть внешний отрезок касательной
 см.
см.По свойству касательной и секущей запишем:
 ,
,  ,
,
 ,
,  .
.
Тогда (см).
(см).
Ответ: 12 см.
 ,
,  ,
,  ,
,  .
. Тогда
 (см).
(см). Ответ: 12 см.
Пример 6. Дана точка  , удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. В каком отношении точка
, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. В каком отношении точка  делит хорду?
делит хорду?
 , удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. В каком отношении точка
, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. В каком отношении точка  делит хорду?
делит хорду?
Решение. Рассмотрим окружность (рис.8.102) радиуса  см.
см.
Отметим на диаметре точку
точку  так, что
так, что  см,
см,  см.
см.
Через точку проведем хорду
проведем хорду  см.
см.
Тогда, если см, то
см, то  см.
см.
По свойству пересекающихся хорд имеем:
 ,
,
 ,
,
 , откуда
, откуда  ,
,  .
.
Получили отрезки длиной 12 см и 6 см.
Тогда .
.
Ответ: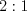 .
.
 см.
см. Отметим на диаметре
 точку
точку  так, что
так, что  см,
см,  см.
см. Через точку
 проведем хорду
проведем хорду  см.
см. Тогда, если
 см, то
см, то  см.
см. По свойству пересекающихся хорд имеем:
 ,
,  ,
,  , откуда
, откуда  ,
,  .
. Получили отрезки длиной 12 см и 6 см.
Тогда
 .
. Ответ:
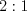 .
.Пример 7. Круг разделен на два сегмента хордой, равной стороне правильного вписанного треугольника. Найдите отношение площадей этих сегментов.

Решение. Рассмотрим круг радиуса  и правильный треугольник
и правильный треугольник  , вписанный в круг (рис. 8.105).
, вписанный в круг (рис. 8.105).
Так как вписанный в окружность угол равен
равен  , то соответствующий ему центральный угол
, то соответствующий ему центральный угол  равен
равен  .
.
По формуле 8.11 найдем площадь треугольника :
:
 .
.
 и правильный треугольник
и правильный треугольник  , вписанный в круг (рис. 8.105).
, вписанный в круг (рис. 8.105). Так как вписанный в окружность угол
 равен
равен  , то соответствующий ему центральный угол
, то соответствующий ему центральный угол  равен
равен  .
. По формуле 8.11 найдем площадь треугольника
 :
:  .
. Найдем площадь сегмента, вычитая из площади сектора  площадь треугольника
площадь треугольника  :
:
 .
.
 площадь треугольника
площадь треугольника  :
:  .
.Найдем площадь второго сегмента, вычитая из площади круга площадь первого сегмента:
 .
.
 .
.Найдем отношение площадей этих сегментов:
 .
.
Ответ: .
.
 .
. Ответ:
 .
.1. Различайте круг и окружность.
В свою очередь:
а) в окружности различайте: центр, радиус, диаметр, хорду, дугу, центральный угол и вписанный угол;
б) в круге различайте: центр, радиус, диаметр, хорду, сектор и сегмент.
В свою очередь:
а) в окружности различайте: центр, радиус, диаметр, хорду, дугу, центральный угол и вписанный угол;
б) в круге различайте: центр, радиус, диаметр, хорду, сектор и сегмент.
2. Из одной точки, не принадлежащей окружности, можно провести две касательные к окружности и множество прямых, которые будут пересекать эту окружность (секущих).
3. Теорема Пифагора: квадрат гипотенузы треугольника равен сумме квадратов его катетов:
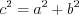 , (8.3)
, (8.3)
где – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.
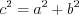 , (8.3)
, (8.3) где
 – гипотенуза,
– гипотенуза,  и
и  – катеты.
– катеты.4. Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих же сторон на косинус угла между ними:
 . (8.4)
. (8.4)
 . (8.4)
. (8.4)5. Площадь треугольника:
 , (8.11)
, (8.11)
где и
и  – стороны,
– стороны,  – величина угла между ними произвольного треугольника.
– величина угла между ними произвольного треугольника.
 , (8.11)
, (8.11) где
 и
и  – стороны,
– стороны,  – величина угла между ними произвольного треугольника.
– величина угла между ними произвольного треугольника.





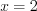



 , откуда
, откуда 
 ,
, 

 .
. 
