Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты






 . (8.2)
. (8.2)
Многоугольником  на плоскости называют фигуру, состоящую из точек
на плоскости называют фигуру, состоящую из точек  и соединяющих их непересекающихся отрезков
и соединяющих их непересекающихся отрезков  .
.
 на плоскости называют фигуру, состоящую из точек
на плоскости называют фигуру, состоящую из точек  и соединяющих их непересекающихся отрезков
и соединяющих их непересекающихся отрезков  .
. Точки  называют вершинами многоугольника, а отрезки
называют вершинами многоугольника, а отрезки  – его сторонами.
– его сторонами.
Две вершины многоугольника называются смежными, если они соединяются стороной многоугольника.
Две стороны многоугольника называются смежными, если они имеют общую вершину.
 называют вершинами многоугольника, а отрезки
называют вершинами многоугольника, а отрезки  – его сторонами.
– его сторонами. Две вершины многоугольника называются смежными, если они соединяются стороной многоугольника.
Две стороны многоугольника называются смежными, если они имеют общую вершину.
Н а п р и м е р, на рисунке 8.21 изображен пятиугольник  .
.
Точки и
и  – его вершины, а отрезки
– его вершины, а отрезки  и
и  – стороны.
– стороны.
Вершины и
и  ,
,  и
и  ,
,  и
и 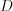 ,
, 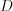 и
и  , а также
, а также  и
и  – смежные.
– смежные.
Стороны и
и  и
и  ,
,  и
и  , а также
, а также  и
и  – смежные.
– смежные.
 .
. Точки
 и
и  – его вершины, а отрезки
– его вершины, а отрезки  и
и  – стороны.
– стороны. Вершины
 и
и  ,
,  и
и  ,
,  и
и 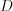 ,
, 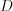 и
и  , а также
, а также  и
и  – смежные.
– смежные. Стороны
 и
и  и
и  ,
,  и
и  , а также
, а также  и
и  – смежные.
– смежные.Диагональю многоугольника называют отрезок, соединяющий две несмежные вершины.
Н а п р и м е р, на рисунке 8.22 из вершины многоугольника
многоугольника  проведены диагонали
проведены диагонали 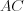 и
и  .
.
Н а п р и м е р, на рисунке 8.22 из вершины
 многоугольника
многоугольника  проведены диагонали
проведены диагонали 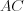 и
и  .
.Многоугольник называют выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую его сторону.
Н а п р и м е р, на рисунке 8.22 изображен выпуклый многоугольник, а на рисунке 8.23 – невыпуклый.
Н а п р и м е р, на рисунке 8.22 изображен выпуклый многоугольник, а на рисунке 8.23 – невыпуклый.
Вершины многоугольника являются вершинами его углов.
Различают внутренние и внешние углы многоугольника.
Н а п р и м е р, пятиугольник , изображенный на рисунке 8.21 имеет пять внутренних углов, которые можно обозначать тремя буквами или одной буквой. Это углы:
, изображенный на рисунке 8.21 имеет пять внутренних углов, которые можно обозначать тремя буквами или одной буквой. Это углы:  и
и  .
.
Различают внутренние и внешние углы многоугольника.
Н а п р и м е р, пятиугольник
 , изображенный на рисунке 8.21 имеет пять внутренних углов, которые можно обозначать тремя буквами или одной буквой. Это углы:
, изображенный на рисунке 8.21 имеет пять внутренних углов, которые можно обозначать тремя буквами или одной буквой. Это углы:  и
и  .
. Внешним углом многоугольника называют угол, смежный с его внутренним углом.
Н а п р и м е р, на рисунке 8.22 угол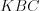 внешний угол при вершине
внешний угол при вершине  многоугольника
многоугольника  .
.
Н а п р и м е р, на рисунке 8.22 угол
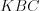 внешний угол при вершине
внешний угол при вершине  многоугольника
многоугольника  .
. Сумму внутренних углов выпуклого многоугольника находят по формуле:
 , (8.1)
, (8.1)
где n – число сторон (углов) многоугольника.
 , (8.1)
, (8.1) где n – число сторон (углов) многоугольника.
Периметром многоугольника называют сумму длин всех его сторон.
Многоугольник называют правильным, если все его стороны и все его углы равны.
Н а п р и м е р, на рисунке 8.24 изображен правильный треугольник, на рисунке 8.25 – правильный четырехугольник, а на рисунке 8.26 – правильный шестиугольник.
Н а п р и м е р, на рисунке 8.24 изображен правильный треугольник, на рисунке 8.25 – правильный четырехугольник, а на рисунке 8.26 – правильный шестиугольник.
Внутренние углы правильного n-угольника находят по формуле:
 . (8.2)
. (8.2)Пример 1. Найдите сумму внутренних угол, внутренние углы и внешние углы правильного треугольника, пятиугольника и шестиугольника.
Решение. 1. По формуле 8.1 найдем сумму внутренних углов треугольника:  .
.
 .
. По формуле 8.2 найдем внутренние углы правильного треугольника:  .
.
 .
.Найдем внешние углы правильного треугольника:  .
.
 .
.2. По формуле 8.1 найдем сумму внутренних углов пятиугольника:  .
.
 .
. По формуле 8.2 найдем внутренние углы правильного пятиугольника:  .
.
 .
.Найдем внешние углы правильного пятиугольника:  .
.
 .
.3. По формуле 8.1 найдем сумму внутренних углов шестиугольника:  .
.
 .
. По формуле 8.2 найдем внутренние углы правильного шестиугольника:  .
.
 .
.Найдем внешние углы правильного шестиугольника:  .
.
 .
.В дальнейшем мы будем рассматривать только выпуклые многоугольники.

