Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
К простейшим геометрическим фигурам на плоскости относят точку и прямую.
Точки обозначают прописными буквами латинского алфавита:
.
Прямые обозначают или строчными буквами латинского алфавита
или двумя прописными буквами: 
и т. д.
Н а п р и м е р, на рисунке 8.1 изображена прямая
и прямая 
. Точка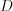 
принадлежит прямой , точка 
не принадлежит данным прямым.
Точки обозначают прописными буквами латинского алфавита:
. Прямые обозначают или строчными буквами латинского алфавита
или двумя прописными буквами: и т. д. Н а п р и м е р, на рисунке 8.1 изображена прямая
и прямая . Точка 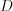принадлежит прямой , точка не принадлежит данным прямым. Часть прямой линии, ограниченную с одной стороны и неограниченную с другой, называют полупрямой или лучом.
Н а п р и м е р, на рисунке 8.2 изображены лучи
и 
.
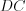Н а п р и м е р, на рисунке 8.2 изображены лучи
и 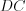. Полупрямые прямой , на которые она разбивается любой точкой прямой, называют дополнительными.
Н а п р и м е р, на рисунке 8.2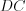 и 
– пара дополнительных полупрямых.
, на которые она разбивается любой точкой прямой, называют дополнительными. Н а п р и м е р, на рисунке 8.2
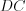и – пара дополнительных полупрямых. Часть прямой линии, ограниченную двумя точками, называют отрезком.
Отрезки называют равными, если их концы совпадают при наложении одного отрезка на другой.
Н а п р и м е р, на рисунке 8.3 изображен отрезок.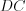
Отрезки называют равными, если их концы совпадают при наложении одного отрезка на другой.
Н а п р и м е р, на рисунке 8.3 изображен отрезок
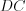. Линию, состоящую из нескольких отрезков, не лежащих на одной прямой (конец предыдущего отрезка совпадает с началом следующего), называют ломаной линией. Отрезки, из которых состоит ломаная линия, называют ее звеньями.
Н а п р и м е р, на рисунке 8.4 изображена ломаная
, состоящая из четырех звеньев: 
и 
.
Н а п р и м е р, на рисунке 8.4 изображена ломаная
, состоящая из четырех звеньев: и . Ломаная называется замкнутой, если ее концы совпадают.
Н а п р и м е р, на рисунках 8.5 и 8.6 изображены замкнутые ломаные.
Н а п р и м е р, на рисунках 8.5 и 8.6 изображены замкнутые ломаные.
Чтобы найти длину ломаной, необходимо найти сумму длин ее звеньев.
Длина отрезка, соединяющего концы ломаной, короче ее длины.
Н а п р и м е р, если
мм, 
мм, 
мм, 
мм, то длина ломаной будет равна 84 мм.
Длина отрезка, соединяющего концы ломаной, короче ее длины.
Н а п р и м е р, если
мм, мм, мм, мм, то длина ломаной будет равна 84 мм.Углом называют фигуру, образованную двумя лучами, исходящими из одной точки (рис. 8.7). Эту точку называют вершиной угла (точка 
), а лучи – сторонами угла (лучи 
и 
).
Угол можно обозначать тремя прописными буквами так, чтобы буква, обозначающая вершину угла, стояла между двумя другими буквами или одной прописной буквой, обозначающей вершину угла.
Н а п р и м е р, на рисунке 8.7 изображен угол
(угол ).
), а лучи – сторонами угла (лучи и ). Угол можно обозначать тремя прописными буквами так, чтобы буква, обозначающая вершину угла, стояла между двумя другими буквами или одной прописной буквой, обозначающей вершину угла.
Н а п р и м е р, на рисунке 8.7 изображен угол
(угол ). Биссектрисой угла называют луч, который выходит из вершины угла и делит этот угол на два равных угла. Каждая точка биссектрисы угла равноудалена от сторон этого угла.
Н а п р и м е р, на рисунке 8.8 луч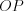
– биссектриса угла , следовательно, углы 
и 
равны, а точка 
равноудалена от сторон угла.
Н а п р и м е р, на рисунке 8.8 луч
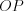– биссектриса угла , следовательно, углы и равны, а точка равноудалена от сторон угла.Угол называют развернутым, если его стороны являются дополнительными прямыми одной прямой. На рисунке 8.9 угол – развернутый.
– развернутый. Основной единицей измерения углов считают угол в 1 градус.
Угол в один градус – это угол, равный
части развернутого угла.
Развернутый угол равен
.
Угол в один градус – это угол, равный
части развернутого угла. Развернутый угол равен
. Наряду с градусной мерой угла употребляется и радианная мера:
n рад =
, а 
рад.
n рад =
, а рад.Н а п р и м е р: 1) 5 рад = 
; 2) 
рад = 
рад.
; 2) рад = рад.Два угла называют смежными, если у них одна сторона общая, а две другие стороны этих углов являются дополнительными полупрямыми.
Сумма смежных углов равна.
Н а п р и м е р, так как углы
и 
являются смежными (рис. 8.10) и 
, то 
.
Сумма смежных углов равна
. Н а п р и м е р, так как углы
и являются смежными (рис. 8.10) и , то . Острым углом называют угол, градусная мера которого меньше 
.
Н а п р и м е р, на рисунке 8.10 угол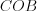
– острый.
. Н а п р и м е р, на рисунке 8.10 угол
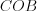– острый. Тупым углом называют угол, градусная мера которого больше , но меньше .
Н а п р и м е р, на рисунке 8.10 угол – тупой.
, но меньше . Н а п р и м е р, на рисунке 8.10 угол
– тупой.Прямым углом называют угол, градусная мера которого равна .
Н а п р и м е р, на рисунке 8.11 угол – прямой.
. Н а п р и м е р, на рисунке 8.11 угол
– прямой.Прямые, которые пересекаются под прямым углом, называют взаимно перпендикулярными.
Н а п р и м е р, на рисунке 8.12 прямые и 
взаимно перпендикулярные. Записывают: 
.
Н а п р и м е р, на рисунке 8.12 прямые
и взаимно перпендикулярные. Записывают: . Две прямые, которые принадлежат одной плоскости и не имеют общих точек, называют параллельными.
Н а п р и м е р, на рисунке 8.12 прямая
параллельна прямой . Записывают: 
.
Н а п р и м е р, на рисунке 8.12 прямая
параллельна прямой . Записывают: .Прямую, которая пересекает данную прямую и не перпендикулярна к ней, называют наклонной.
Точку пересечения наклонной к прямой с этой прямой называют основанием наклонной.
Н а п р и м е р, на рисунке 8.12 прямая
– наклонная к прямой (и к ). Точка 
– основание наклонной к прямой .
Точку пересечения наклонной к прямой с этой прямой называют основанием наклонной.
Н а п р и м е р, на рисунке 8.12 прямая
– наклонная к прямой (и к ). Точка – основание наклонной к прямой .Через точку, не принадлежащую прямой, можно провести единственную прямую, перпендикулярную этой прямой, и бесчисленное множество прямых, которые пересекают эту прямую и образуют с ней непрямые углы.
Н а п р и м е р, на рисунке 8.13 через точку
проведены наклонные 
и к прямой .
Н а п р и м е р, на рисунке 8.13 через точку
проведены наклонные и к прямой . Из точки, не принадлежащей прямой, можно провести к этой прямой только один перпендикуляр.
Точку пересечения перпендикуляра к прямой с этой прямой называют основанием перпендикуляра.
Н а п р и м е р, на рисунке 8.14 из точки к прямой проведен перпендикуляр. Точка 
– основание этого перпендикуляра.
Точку пересечения перпендикуляра к прямой с этой прямой называют основанием перпендикуляра.
Н а п р и м е р, на рисунке 8.14 из точки
к прямой проведен перпендикуляр. Точка – основание этого перпендикуляра.Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных из одной точки к прямой, называют проекцией отрезка наклонной на эту прямую.
Расстоянием от точки до прямой называют длину перпендикуляра от данной точки до его основания на данной прямой.
Н а п р и м е р, на рисунке 8.15 отрезок – проекция отрезка наклонной к прямой . Расстояние от точки до прямой равно длине отрезка 
.
Расстоянием от точки до прямой называют длину перпендикуляра от данной точки до его основания на данной прямой.
Н а п р и м е р, на рисунке 8.15 отрезок
– проекция отрезка наклонной к прямой . Расстояние от точки до прямой равно длине отрезка .Серединным перпендикуляром к отрезку называют перпендикуляр, проведенный через середину этого отрезка.
Каждая точка серединного перпендикуляра к отрезку, равноудалена от концов этого отрезка.
Н а п р и м е р, на рисунке 8.16
и 
так как – серединный перпендикуляр к отрезку 
.
Каждая точка серединного перпендикуляра к отрезку, равноудалена от концов этого отрезка.
Н а п р и м е р, на рисунке 8.16
и так как – серединный перпендикуляр к отрезку .В результате пересечения двух прямых получаем две пары вертикальных углов.
Два угла называют вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вертикальные углы равны.
Н а п р и м е р, на рисунке 8.17 углы и 
, а также углы 
и 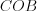– пары вертикальных углов, причем 
и 
.
Два угла называют вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вертикальные углы равны.
Н а п р и м е р, на рисунке 8.17 углы
и , а также углы и 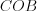– пары вертикальных углов, причем и . Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Н а п р и м е р, на рисунке 8.18 через точки
и прямой 
проведены параллельные прямые 
и 
. Так как 
, то 
.
Н а п р и м е р, на рисунке 8.18 через точки
и прямой проведены параллельные прямые и . Так как , то .Если две прямые и (рис. 8.19) пересечь третьей прямой (секущей), то получим:
1) внутренние односторонние углы: 3 и 5, 4 и 6;
2) внутренние накрест лежащие углы: 3 и 6, 4 и 5;
3) соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8.
и (рис. 8.19) пересечь третьей прямой (секущей), то получим: 1) внутренние односторонние углы: 3 и 5, 4 и 6;
2) внутренние накрест лежащие углы: 3 и 6, 4 и 5;
3) соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8.
Если две параллельные прямые и (рис. 8.20) пересечь третьей прямой 
, то:
1) накрест лежащие углы будут равны (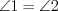
и 
);
2) сумма внутренних односторонних углов будет равна
(
и 
);
3) соответственные углы будут равны (например,
).
и (рис. 8.20) пересечь третьей прямой , то: 1) накрест лежащие углы будут равны (
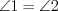и ); 2) сумма внутренних односторонних углов будет равна
(
и ); 3) соответственные углы будут равны (например,
).Признаки параллельности прямых:
1) если прямая с параллельна прямым и , то прямые и параллельны;
и , то прямые и параллельны; 2) если внутренние накрест лежащие углы прямых и с секущей равны, или сумма внутренних односторонних углов равна , или соответственные углы равны, то прямые и параллельны.
и с секущей равны, или сумма внутренних односторонних углов равна , или соответственные углы равны, то прямые и параллельны.Пример 1. На рисунке 8.20 прямые и параллельные, а угол 
равен 
. Найдите углы 
и 
.
и параллельные, а угол равен . Найдите углы и .Решение. Если угол равен , то угол 
также равен как накрест лежащий с ним.
равен , то угол также равен как накрест лежащий с ним.Углы и 
, а также углы и 
образуют пары вертикальных углов, следовательно,
.
и , а также углы и образуют пары вертикальных углов, следовательно, .Углы и , а также 
и 
образуют пары внутренних односторонних углов, значит
.
и , а также и образуют пары внутренних односторонних углов, значит .1. Прямые на плоскости могут: пересекаться, быть параллельными, совпадать.
2. При определенном расположении прямых могут быть образованы углы: смежные, вертикальные, накрест лежащие, односторонние, соответственные.
3. Некоторые аксиомы планиметрии:
1) Через две точки можно провести прямую линию и притом только одну.
2) Отрезок прямой короче всякой другой линии (ломаной или кривой), соединяющей его концы.
3) Через точку, не принадлежащую прямой, можно провести только одну прямую, параллельную данной прямой.