Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты



 .
. .
. ,
,  ,
,  .
.
Тригонометрическими называют неравенства, содержащие тригонометрические функции.
К простейшим тригонометрическим неравенствам относят неравенства вида:  ,
,  ,
,  ,
, 
 .
.
 ,
,  ,
,  ,
, 
 .
.Методы решений неравенств
1. Решение тригонометрических неравенств с помощью единичной окружности.
2. Графическое решение тригонометрических неравенств.
3. Решение неравенств методом интервалов.
Решая тригонометрические неравенства методом интервалов, необходимо отметить, что в случае, если исходное неравенство удалось свести к простейшему, то отбирать корни соответствующего простейшего уравнения (а значит и решать неравенство), будем на основном периоде тригонометрической функции.
Основной период  тригонометрической функции
тригонометрической функции  можно определить по формуле
можно определить по формуле  , где
, где  – основной период функции
– основной период функции  .
.
 тригонометрической функции
тригонометрической функции  можно определить по формуле
можно определить по формуле  , где
, где  – основной период функции
– основной период функции  .
. Например:
1) основной период  функции
функции  равен
равен  , так как основной период
, так как основной период  функции
функции  равен
равен  , а
, а 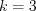 ;
;
 функции
функции  равен
равен  , так как основной период
, так как основной период  функции
функции  равен
равен  , а
, а 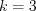 ;
; 2) основной период  функции
функции  равен
равен  , так как основной период
, так как основной период  функции
функции 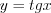 равен
равен  , а
, а  .
.
 функции
функции  равен
равен  , так как основной период
, так как основной период  функции
функции 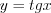 равен
равен  , а
, а  .
. Пример 1. Решите неравенство  .
.
 .
. Решение. Найдем наименьшее положительное решение уравнения  . Получим:
. Получим:  . Построим на координатной плоскости единичную окружность и прямую
. Построим на координатной плоскости единичную окружность и прямую  (рис. 7.53).
(рис. 7.53).
 . Получим:
. Получим:  . Построим на координатной плоскости единичную окружность и прямую
. Построим на координатной плоскости единичную окружность и прямую  (рис. 7.53).
(рис. 7.53).
Решением данного неравенства на основном периоде функции  , равном
, равном  , являются те значения переменной
, являются те значения переменной  , при которых выполняется условие
, при которых выполняется условие  , т. е. отрезок
, т. е. отрезок ![\left [ \frac{3\pi}{4} ; 2\pi +\frac{\pi}{4}\right ] LaTeX formula: \left [ \frac{3\pi}{4} ; 2\pi +\frac{\pi}{4}\right ]](/uploads/formulas/8e79c9cb890cc7828d62d77d2e4e63d60af41c88.1.1.png) . Прибавляя к концам отрезка числа вида
. Прибавляя к концам отрезка числа вида  , где
, где  , получим множество всех решений неравенства.
, получим множество всех решений неравенства.
 , равном
, равном  , являются те значения переменной
, являются те значения переменной  , при которых выполняется условие
, при которых выполняется условие  , т. е. отрезок
, т. е. отрезок ![\left [ \frac{3\pi}{4} ; 2\pi +\frac{\pi}{4}\right ] LaTeX formula: \left [ \frac{3\pi}{4} ; 2\pi +\frac{\pi}{4}\right ]](/uploads/formulas/8e79c9cb890cc7828d62d77d2e4e63d60af41c88.1.1.png) . Прибавляя к концам отрезка числа вида
. Прибавляя к концам отрезка числа вида  , где
, где  , получим множество всех решений неравенства.
, получим множество всех решений неравенства. Ответ: ![\left [ \frac{3\pi}{4}+2\pi n;\frac{9\pi}{4}+2\pi n\right ] LaTeX formula: \left [ \frac{3\pi}{4}+2\pi n;\frac{9\pi}{4}+2\pi n\right ]](/uploads/formulas/142ca63f3bdc324ee4e30096b4126e802ad00bf9.1.1.png) ,
,  .
.
![\left [ \frac{3\pi}{4}+2\pi n;\frac{9\pi}{4}+2\pi n\right ] LaTeX formula: \left [ \frac{3\pi}{4}+2\pi n;\frac{9\pi}{4}+2\pi n\right ]](/uploads/formulas/142ca63f3bdc324ee4e30096b4126e802ad00bf9.1.1.png) ,
,  .
. Пример 2. Решите неравенство  .
.
 .
. Решение. Построим графики функций 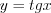 и
и  на промежутке
на промежутке  , т. е. на основном периоде функции
, т. е. на основном периоде функции 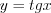 (рис. 7.54).
(рис. 7.54).
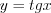 и
и  на промежутке
на промежутке  , т. е. на основном периоде функции
, т. е. на основном периоде функции 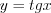 (рис. 7.54).
(рис. 7.54). 
Решением данного неравенства на этом промежутке является множество тех значений переменной  , при которых график функции
, при которых график функции 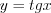 расположен не выше прямой
расположен не выше прямой  : промежуток
: промежуток ![\left ( -\frac{\pi}{2};\frac{\pi}{4} \right ] LaTeX formula: \left ( -\frac{\pi}{2};\frac{\pi}{4} \right ]](/uploads/formulas/51480eb01dd950729e0472c6d9fb7c0f0bcdd845.1.1.png) . Прибавляя к концам этого промежутка числа вида
. Прибавляя к концам этого промежутка числа вида  , где
, где  , получим множество всех решений данного неравенства.
, получим множество всех решений данного неравенства.
 , при которых график функции
, при которых график функции 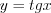 расположен не выше прямой
расположен не выше прямой  : промежуток
: промежуток ![\left ( -\frac{\pi}{2};\frac{\pi}{4} \right ] LaTeX formula: \left ( -\frac{\pi}{2};\frac{\pi}{4} \right ]](/uploads/formulas/51480eb01dd950729e0472c6d9fb7c0f0bcdd845.1.1.png) . Прибавляя к концам этого промежутка числа вида
. Прибавляя к концам этого промежутка числа вида  , где
, где  , получим множество всех решений данного неравенства.
, получим множество всех решений данного неравенства. Ответ: ![\left ( -\frac{\pi}{2}+\pi n;\frac{\pi}{4} +\pi n\right ] LaTeX formula: \left ( -\frac{\pi}{2}+\pi n;\frac{\pi}{4} +\pi n\right ]](/uploads/formulas/c1a23c0950ed498e52202752df9dc64ff94691d6.1.1.png) ,
,  .
.
![\left ( -\frac{\pi}{2}+\pi n;\frac{\pi}{4} +\pi n\right ] LaTeX formula: \left ( -\frac{\pi}{2}+\pi n;\frac{\pi}{4} +\pi n\right ]](/uploads/formulas/c1a23c0950ed498e52202752df9dc64ff94691d6.1.1.png) ,
,  .
.Пример 3. Решите неравенство  .
.
 .
.Решение. 1. Запишем неравенство в виде  и рассмотрим функцию
и рассмотрим функцию  .
.
 и рассмотрим функцию
и рассмотрим функцию  .
. 2. Определим основной период функции по формуле  . Зная, что основной период
. Зная, что основной период  функции
функции  равен
равен  , а
, а  , получим
, получим  .
.
 . Зная, что основной период
. Зная, что основной период  функции
функции  равен
равен  , а
, а  , получим
, получим  .
. 3. Найдем нули функции, решая уравнение:
 , откуда
, откуда  ,
,  ;
;  ,
,  .
.
 , откуда
, откуда  ,
,  ;
;  ,
,  .
.4. Отберем корни уравнения на отрезке ![\left [ 0;\pi \right ] LaTeX formula: \left [ 0;\pi \right ]](/uploads/formulas/ff05a4b242fbad807a5a5234fcc7073c57e0ac75.1.1.png) :
:
если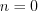 , то
, то  ; если
; если  , то
, то  .
.
![\left [ 0;\pi \right ] LaTeX formula: \left [ 0;\pi \right ]](/uploads/formulas/ff05a4b242fbad807a5a5234fcc7073c57e0ac75.1.1.png) :
: если
 , то
, то  ; если
; если  , то
, то  .
. 5. Нанесем числа  и
и  на отрезок
на отрезок ![\left [ 0;\pi \right ] LaTeX formula: \left [ 0;\pi \right ]](/uploads/formulas/ff05a4b242fbad807a5a5234fcc7073c57e0ac75.1.1.png) и определим знаки значений функции на полученных промежутках (рис. 7.55).
и определим знаки значений функции на полученных промежутках (рис. 7.55).
 и
и  на отрезок
на отрезок ![\left [ 0;\pi \right ] LaTeX formula: \left [ 0;\pi \right ]](/uploads/formulas/ff05a4b242fbad807a5a5234fcc7073c57e0ac75.1.1.png) и определим знаки значений функции на полученных промежутках (рис. 7.55).
и определим знаки значений функции на полученных промежутках (рис. 7.55).
6. Решением неравенства на отрезке является промежуток, на котором функция принимает неположительные значения, т. е. отрезок ![\left [ \frac{\pi}{4};\frac{3\pi}{4} \right ] LaTeX formula: \left [ \frac{\pi}{4};\frac{3\pi}{4} \right ]](/uploads/formulas/3192c1e505bc5096194a845861ef362752570f38.1.1.png) .
.
Чтобы записать множество всех решений неравенства, необходимо к концам этого отрезка прибавить период функции , предварительно умноженный на число m, принадлежащее множеству всех целых чисел.
, предварительно умноженный на число m, принадлежащее множеству всех целых чисел.
![\left [ \frac{\pi}{4};\frac{3\pi}{4} \right ] LaTeX formula: \left [ \frac{\pi}{4};\frac{3\pi}{4} \right ]](/uploads/formulas/3192c1e505bc5096194a845861ef362752570f38.1.1.png) .
. Чтобы записать множество всех решений неравенства, необходимо к концам этого отрезка прибавить период функции
 , предварительно умноженный на число m, принадлежащее множеству всех целых чисел.
, предварительно умноженный на число m, принадлежащее множеству всех целых чисел. Ответ: ![\left [ \frac{\pi}{4}+\pi m;\frac{3\pi}{4}+\pi m\right ] LaTeX formula: \left [ \frac{\pi}{4}+\pi m;\frac{3\pi}{4}+\pi m\right ]](/uploads/formulas/4532567d8c09eae613956967e11fe0d8a14d2811.1.1.png) ,
, 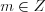 .
.
![\left [ \frac{\pi}{4}+\pi m;\frac{3\pi}{4}+\pi m\right ] LaTeX formula: \left [ \frac{\pi}{4}+\pi m;\frac{3\pi}{4}+\pi m\right ]](/uploads/formulas/4532567d8c09eae613956967e11fe0d8a14d2811.1.1.png) ,
, 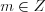 .
. Пример 4. Найдите решения неравенства
 .
.Решение. 1. Запишем неравенство в виде
 .
.Применяя формулы  и
и  , получим:
, получим:
 и
и  , получим:
, получим: ,
,  ,
,  .
.2. Рассмотрим функцию  и найдем ее нули, решая уравнение
и найдем ее нули, решая уравнение  , равносильное совокупности уравнений:
, равносильное совокупности уравнений:
1) ,
,  ,
,  ;
;  ,
,  ;
;
 и найдем ее нули, решая уравнение
и найдем ее нули, решая уравнение  , равносильное совокупности уравнений:
, равносильное совокупности уравнений: 1)
 ,
,  ,
,  ;
;  ,
,  ;
; 2)  ,
,  ,
,  ,
, 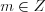 ;
;  ,
, 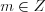 .
.
 ,
,  ,
,  ,
, 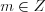 ;
;  ,
, 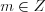 .
.3. Отберем последовательные корни уравнения:
1) если 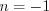 , то
, то  ; если
; если 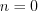 , то
, то  ; если
; если  , то
, то  ; если
; если  , то
, то  ;
;
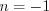 , то
, то  ; если
; если 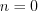 , то
, то  ; если
; если  , то
, то  ; если
; если  , то
, то  ;
; 2) если  , то
, то  ; если
; если 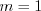 , то
, то  ; если
; если  , то
, то  ; если
; если  , то
, то  .
.
 , то
, то  ; если
; если 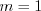 , то
, то  ; если
; если  , то
, то  ; если
; если  , то
, то  .
.4. Нанесем корни уравнения на координатную прямую и определим знаки значений функции  на полученных промежутках (рис. 7.56).
на полученных промежутках (рис. 7.56).
 на полученных промежутках (рис. 7.56).
на полученных промежутках (рис. 7.56).
5. Из рисунка 7.56 видим, что отрицательные значения функция принимает на промежутках разной длины:
1) длина промежутка  и промежутка
и промежутка  равна
равна  ;
;
 и промежутка
и промежутка  равна
равна  ;
; 2) длина промежутка  и промежутка
и промежутка  равна
равна  .
.
 и промежутка
и промежутка  равна
равна  .
. Так как все промежутки знакопостоянства функции повторяются через  , то основной период функции равен
, то основной период функции равен  .
.
Чтобы записать все решения неравенства необходимо к концам промежутков, на которых функция принимает отрицательные значения, прибавить , где
, где  .
.
 , то основной период функции равен
, то основной период функции равен  .
. Чтобы записать все решения неравенства необходимо к концам промежутков, на которых функция принимает отрицательные значения, прибавить
 , где
, где  .
. Ответ:  ;
;  ,
,  .
.
 ;
;  ,
,  .
.Если основной период функции, записанной в левой части неравенства, определить сложно, то можно решать неравенство на любом периоде этой функции. В отдельных случаях можно воспользоваться следующим алгоритмом:
1) записать неравенство в виде 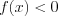
 и найти нули функции, решая уравнение
и найти нули функции, решая уравнение  ;
;
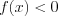
 и найти нули функции, решая уравнение
и найти нули функции, решая уравнение  ;
;2) отобрать несколько последовательных корней уравнения  так, чтобы получить не менее двух промежутков, на которых значения функции отрицательные (положительные, неположительные, неотрицательные);
так, чтобы получить не менее двух промежутков, на которых значения функции отрицательные (положительные, неположительные, неотрицательные);
 так, чтобы получить не менее двух промежутков, на которых значения функции отрицательные (положительные, неположительные, неотрицательные);
так, чтобы получить не менее двух промежутков, на которых значения функции отрицательные (положительные, неположительные, неотрицательные);3) определить два последовательных промежутка, на которых значения функции отрицательные (положительные, неположительные, неотрицательные);
4) определить расстояние на координатной прямой между промежутками, на которых функция имеет значения одного и того же знака (период функции), вычитая из начала второго промежутка, начало первого;
5) записать один из промежутков, на котором функция принимает отрицательные (положительные, неположительные, неотрицательные) значения, и к его концам прибавить период функции, умноженный на целое число n.

