Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
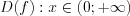 ;
; 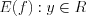 .
. 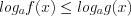 (
( ,
,  ,
,  ), (7.17) где
), (7.17) где 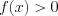 и
и 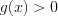 то:
то: 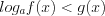 (7.18) и
(7.18) и 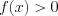 , то:
, то: 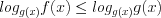 , (7.19)
, (7.19)
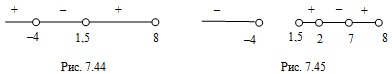
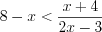 ,
, 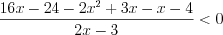 ,
,  ,
, 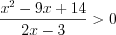 .
. 
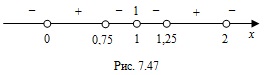
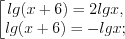
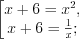

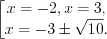
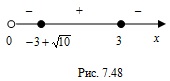
Логарифмическими называют неравенства, содержащие логарифмическую функцию.
Решение логарифмических неравенств основано на свойствах логарифмической функции.
Логарифмической называют функцию вида 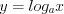 , где
, где  и
и  .
.
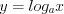 , где
, где  и
и  .
. 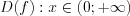 ;
; 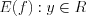 .
. При  функция возрастает, а при
функция возрастает, а при  – убывает.
– убывает.
 функция возрастает, а при
функция возрастает, а при  – убывает.
– убывает.Методы решений неравенств
1. Если неравенство имеет вид
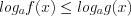 (
( ,
,  ,
,  ), (7.17) где
), (7.17) где 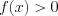 и
и 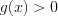 то:
то: а) при условии, что  получим
получим 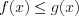 ; (7.17.1)
; (7.17.1)
 получим
получим 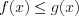 ; (7.17.1)
; (7.17.1)б) при условии, что  получим
получим 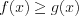 . (7.17.2)
. (7.17.2)
 получим
получим 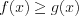 . (7.17.2)
. (7.17.2)2. Если неравенство имеет вид
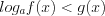 (7.18) и
(7.18) и 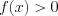 , то:
, то: а) при условии, что  получим
получим 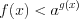 ; (7.18.1)
; (7.18.1)
 получим
получим 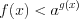 ; (7.18.1)
; (7.18.1)б) при условии, что  получим
получим 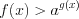 . (7.18.2)
. (7.18.2)
 получим
получим 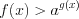 . (7.18.2)
. (7.18.2)3. Если неравенство имеет вид
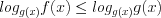 , (7.19)
, (7.19)то решают совокупность систем неравенств:
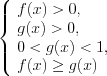 (7.19.1) и
(7.19.1) и  (7.19.2)
(7.19.2)
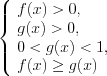 (7.19.1) и
(7.19.1) и  (7.19.2)
(7.19.2)Пример 1. Найдите решение неравенства  .
.
 .
.Решение. ОДЗ: 

Поскольку решением первого неравенства является промежуток 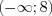 , то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем:
, то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем: 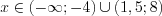 .
.
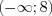 , то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем:
, то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем: 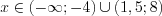 .
.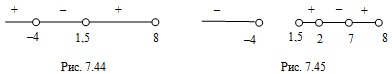
Так как 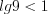 , то :
, то :
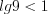 , то :
, то : 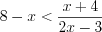 ,
, 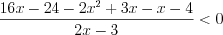 ,
,  ,
, 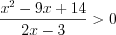 .
. Решим последнее неравенство методом интервалов на ОДЗ исходного неравенства (рис. 7.45) и получим: 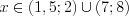 .
.
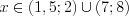 .
. Ответ: 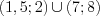 .
.
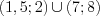 .
.Пример 2. Найдите середину промежутка, на котором выполняется неравенство 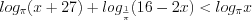 .
.
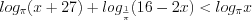 .
.Решение. ОДЗ: 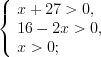
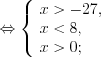
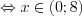 .
.
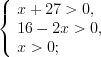
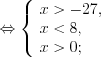
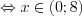 .
.Выполним преобразования:
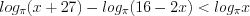
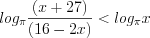 .
.
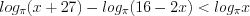
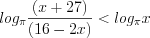 .
. Поскольку основание логарифма 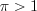 , то данное неравенство равносильно неравенству:
, то данное неравенство равносильно неравенству:
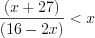 ,
, 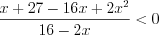 ,
, 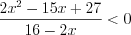 .
.
Решение этого неравенства показано на рисунке 7.46 : .
.
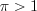 , то данное неравенство равносильно неравенству:
, то данное неравенство равносильно неравенству: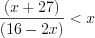 ,
, 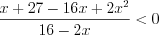 ,
, 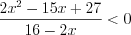 .
. Решение этого неравенства показано на рисунке 7.46 :
 .
.
Найдем середину интервала: 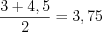 .
.
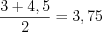 .
.Ответ: 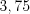 .
.
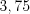 .
.Пример 3. Решите неравенство 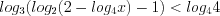 .
.
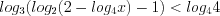 .
.Решение. ОДЗ: 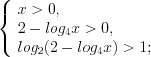
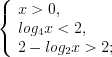
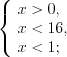
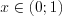 .
.
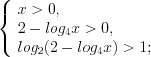
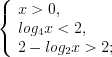
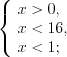
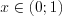 .
.Учитывая, что  , получим:
, получим:
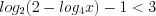 ,
, 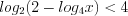 ,
, 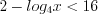 ,
,  ,
, 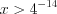 ,
, 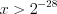 .
.
Учитывая ОДЗ неравенства, запишем его решение: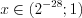 .
.
 , получим:
, получим: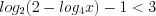 ,
, 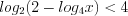 ,
, 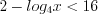 ,
,  ,
, 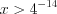 ,
, 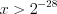 .
. Учитывая ОДЗ неравенства, запишем его решение:
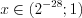 .
.Ответ: 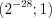 .
.
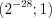 .
.Пример 4. Найдите наименьшее натуральное число, которое не является решением неравенства 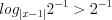 .
.
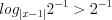 .
.1. Рассмотрим функцию 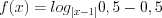 .
.
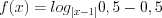 .
.2. 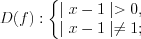
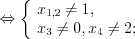
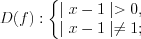
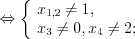
3. Найдем нули функции, решая уравнение
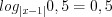 , откуда
, откуда 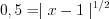 ,
, 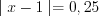 .
.
Тогда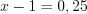 или
или 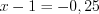 , а
, а 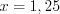 или
или 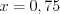 .
.
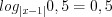 , откуда
, откуда 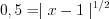 ,
, 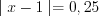 .
. Тогда
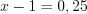 или
или 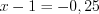 , а
, а 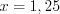 или
или 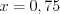 .
.4. Нанесем нули функции на ее область определения и установим знаки значений функции на полученных промежутках (рис. 7.47).
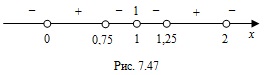
5. Решением неравенства являются промежутки, на которых функция положительна: 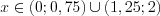 . Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
. Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
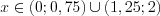 . Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
. Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.Ответ: 1.
Пример 5. Найдите среднее арифметическое всех целых решений неравенства 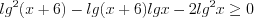 .
.
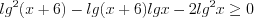 .
.Решение. ОДЗ: 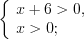
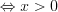 .
.
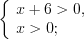
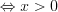 .
. По теореме, обратной теореме Виета, найдем нули функции 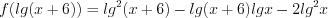 .
.
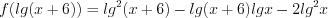 .
. 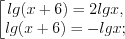
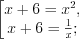

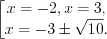
Согласно рисунку 7.48 запишем его решение:  .
.
 .
.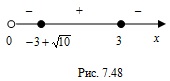
Запишем целые решения неравенства: 1; 2; 3. Найдем среднее арифметическое этих решений: 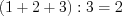 .
.
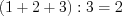 .
.Ответ: 2.
Всякое логарифмическое неравенство можно решить методом интервалов, но наиболее целесообразно этот метод применять в случае решения неравенств 7.19 и комбинированных неравенств.


 равносильно
равносильно