Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
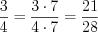 ,
, 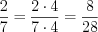 .
.
Обыкновенная дробь – это число вида 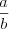 , где
, где  и
и  – натуральные числа.
– натуральные числа.
Число называется знаменателем дроби и показывает, на сколько равных частей разделена единица.
называется знаменателем дроби и показывает, на сколько равных частей разделена единица.
Число называется числителем дроби и показывает, сколько таких частей взято.
называется числителем дроби и показывает, сколько таких частей взято.
Если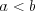 , то дробь
, то дробь 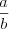 правильная, если
правильная, если 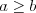 , то дробь
, то дробь 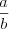 неправильная.
неправильная.
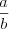 , где
, где  и
и  – натуральные числа.
– натуральные числа. Число
 называется знаменателем дроби и показывает, на сколько равных частей разделена единица.
называется знаменателем дроби и показывает, на сколько равных частей разделена единица. Число
 называется числителем дроби и показывает, сколько таких частей взято.
называется числителем дроби и показывает, сколько таких частей взято. Если
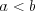 , то дробь
, то дробь 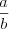 правильная, если
правильная, если 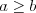 , то дробь
, то дробь 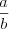 неправильная.
неправильная. Н а п р и м е р, дроби  и
и 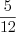 – правильные, а дроби
– правильные, а дроби 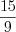 и
и  – неправильные.
– неправильные.
 и
и 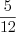 – правильные, а дроби
– правильные, а дроби 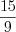 и
и  – неправильные.
– неправильные.Основное свойство дроби: если числитель и знаменатель дроби увеличить или уменьшить в одно и то же число раз, то величина дроби не изменится.
Н а п р и м е р,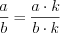 и
и 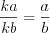 .
.
Н а п р и м е р,
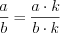 и
и 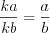 .
.Дробь несократима, если числитель и знаменатель этой дроби представлены взаимно простыми числами.
Н а п р и м е р, дроби и
и 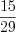 – несократимые, а дроби
– несократимые, а дроби 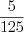 и
и  – сократимые.
– сократимые.
Н а п р и м е р, дроби
 и
и 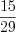 – несократимые, а дроби
– несократимые, а дроби 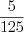 и
и  – сократимые.
– сократимые.Числа вида 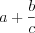 называют смешанными.
называют смешанными.
Как правило, в записи этих чисел знак « » между целой и дробной частью числа опускают.
» между целой и дробной частью числа опускают.
Н а п р и м е р, .
.
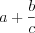 называют смешанными.
называют смешанными. Как правило, в записи этих чисел знак «
 » между целой и дробной частью числа опускают.
» между целой и дробной частью числа опускают. Н а п р и м е р,
 .
.Всякое смешанное число можно представить в виде обыкновенной дроби: 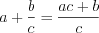 .
.
Н а п р и м е р,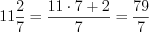 .
.
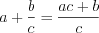 .
. Н а п р и м е р,
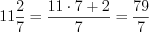 .
.У обыкновенной дроби всегда можно выделить целую часть.
Н а п р и м е р, у правильной дроби целая часть равна нулю; у неправильной дроби
целая часть равна нулю; у неправильной дроби  целая часть равна
целая часть равна  , т.е.
, т.е. 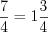 .
.
Н а п р и м е р, у правильной дроби
 целая часть равна нулю; у неправильной дроби
целая часть равна нулю; у неправильной дроби  целая часть равна
целая часть равна  , т.е.
, т.е. 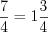 .
.Правила сложения и вычитания обыкновенных дробей
1. Если дроби имеют одинаковые знаменатели, то их складывают (вычитают) по правилу:
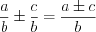 .
.
Н а п р и м е р,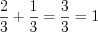 .
.
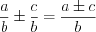 .
. Н а п р и м е р,
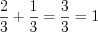 .
. 2. Если дроби имеют различные знаменатели, то их складывают (вычитают) по правилу:
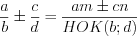 ,
,
где и
и  – дополнительные множители, причем
– дополнительные множители, причем 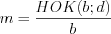 ,
, 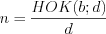 .
.
Н а п р и м е р,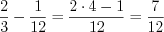 .
.
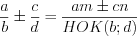 ,
, где
 и
и  – дополнительные множители, причем
– дополнительные множители, причем 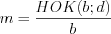 ,
, 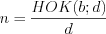 .
. Н а п р и м е р,
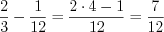 .
.3. При сложении и вычитании смешанных чисел, можно отдельно сложить (вычесть) целые и дробные их части.
Н а п р и м е р,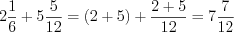 .
.
Н а п р и м е р,
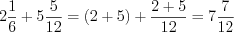 .
.Правила умножения и деления обыкновенных дробей
1. Умножение дробей выполняют по правилу:
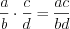 .
.
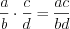 .
. 2. Деление дробей выполняют по правилу:
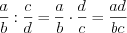 .
.
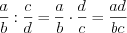 .
.3. При умножении и делении смешанных чисел необходимо представлять эти числа в виде обыкновенных дробей.
Дроби 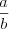 и
и  являются взаимно обратными. Произведение взаимно обратных дробей равно единице:
являются взаимно обратными. Произведение взаимно обратных дробей равно единице: 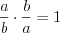 .
.
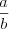 и
и  являются взаимно обратными. Произведение взаимно обратных дробей равно единице:
являются взаимно обратными. Произведение взаимно обратных дробей равно единице: 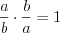 .
.Правило нахождения дроби от числа: чтобы найти дробь от числа, необходимо умножить это число на дробь.
Правило нахождения числа по его дроби: чтобы найти число по заданной величине его дроби, необходимо разделить заданную величину на эту дробь.
Сравнение обыкновенных дробей
1. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой больший числитель.
Н а п р и м е р: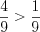 .
.
Н а п р и м е р:
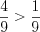 .
.2. Из двух дробей с одинаковыми числителями больше та дробь, у которой меньший знаменатель.
Н а п р и м е р,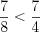 .
.
Н а п р и м е р,
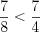 .
.3. При сравнении дробей с различными знаменателями, необходимо их приводить к общему знаменателю.
4. При сравнении смешанных чисел с разными целыми частями достаточно сравнить их целые части.
Н а п р и м е р,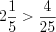 , так как
, так как 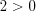 .
.
Н а п р и м е р,
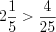 , так как
, так как 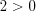 .
.5. При сравнении смешанных чисел с одинаковыми целыми частями необходимо сравнить их дробные части.
Н а п р и м е р,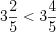 , так как
, так как 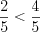 .
.
Н а п р и м е р,
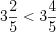 , так как
, так как 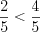 .
.Пример 1. Выполните действия:
1) 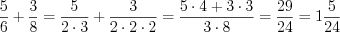 ;
;
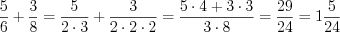 ;
;2) 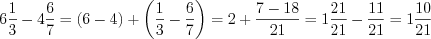 ;
;
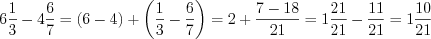 ;
;3) 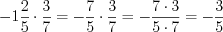 ;
;
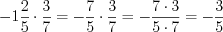 ;
; 4) 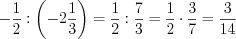 .
.
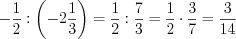 .
.Пример 2. Сравните дроби  и
и  .
.
 и
и  .
.Решение. Приведем эти дроби к знаменателю  :
:
 :
: 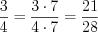 ,
, 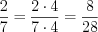 .
. Так как  , то
, то  .
.
 , то
, то  .
.Пример 3. Найдите  от числа
от числа 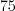 .
.
 от числа
от числа 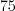 .
.Решение. 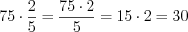 .
.
Ответ: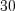 .
.
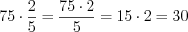 .
. Ответ:
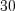 .
.Пример 4. Найдите число,  которого равны
которого равны 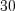 .
.
 которого равны
которого равны 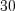 .
.Решение. 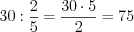 .
.
Ответ: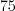 .
.
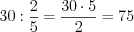 .
. Ответ:
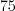 .
.1. Любое натуральное и любое целое число можно представить в виде обыкновенной дроби:
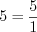 ;
; 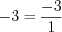 ;
; 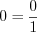 .
.
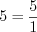 ;
; 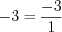 ;
; 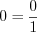 .
.2. Число  всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю:
всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю:
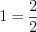 ,
, 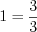 .
.
Исключение составляет дробь . Это выражение не имеет смысла.
. Это выражение не имеет смысла.
 всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю:
всегда можно представить в виде обыкновенной дроби, у которой числитель равен знаменателю: 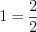 ,
, 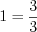 .
. Исключение составляет дробь
 . Это выражение не имеет смысла.
. Это выражение не имеет смысла.3. Целое число (за исключением числа  ) можно всегда представить в виде смешанного числа:
) можно всегда представить в виде смешанного числа:
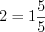 .
.
 ) можно всегда представить в виде смешанного числа:
) можно всегда представить в виде смешанного числа: 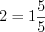 .
.
