Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 , если
, если  и
и  , если
, если  .
. (7.8.1)
(7.8.1)  (7.9.1)
(7.9.1)








![\Leftrightarrow x\in [-3,6; 3] LaTeX formula: \Leftrightarrow x\in [-3,6; 3]](/uploads/formulas/d21e569addc93751b251d3a817fe04fff55cf30b.1.1.png) ;
; 


![\Leftrightarrow x\in (-\infty;-3,6]\cup [3;+\infty) LaTeX formula: \Leftrightarrow x\in (-\infty;-3,6]\cup [3;+\infty)](/uploads/formulas/b2dc53bd5d7853b544c5cb1a9caea247c2c59bb6.1.1.png) .
.




 ,
,  .
.
Преобразования неравенств, содержащих переменную под знаком модуля, основано на определении модуля числа.
Модулем (абсолютной величиной) числа  называют число
называют число  , если оно неотрицательное, и противоположное ему число, если число
, если оно неотрицательное, и противоположное ему число, если число  отрицательное:
отрицательное:
 называют число
называют число  , если оно неотрицательное, и противоположное ему число, если число
, если оно неотрицательное, и противоположное ему число, если число  отрицательное:
отрицательное:  , если
, если  и
и  , если
, если  .
.Методы решений неравенств
1. Если неравенство имеет вид  , (7.8)
, (7.8)
то оно равносильно системе неравенств
 , (7.8)
, (7.8) то оно равносильно системе неравенств
 (7.8.1)
(7.8.1)2. Если неравенство имеет вид  , (7.9)
, (7.9)
то оно равносильно совокупности неравенств
 , (7.9)
, (7.9) то оно равносильно совокупности неравенств
 (7.9.1)
(7.9.1)3. Решение неравенств вида  (
(  ,
,  ,
,  ):
):
 (
(  ,
,  ,
,  ):
):1) если неравенство имеет вид  (
(  ), (7.10)
), (7.10)
то оно равносильно неравенству (
(  ); (7.10.1)
); (7.10.1)
 (
(  ), (7.10)
), (7.10) то оно равносильно неравенству
 (
(  ); (7.10.1)
); (7.10.1)2) если неравенство имеет вид  , (7.11)
, (7.11)
то оно выполняется на всей области определения функции ;
;
 , (7.11)
, (7.11) то оно выполняется на всей области определения функции
 ;
;3) если неравенство имеет вид  , (7.12)
, (7.12)
то оно равносильно неравенству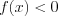 . (7.12.1)
. (7.12.1)
 , (7.12)
, (7.12) то оно равносильно неравенству
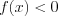 . (7.12.1)
. (7.12.1)4. Если неравенство имеет вид  (
(  ,
,  ,
,  ), (7.13)
), (7.13)
то оно равносильно неравенству (
(  ,
,  ,
,  ). (7.13.1)
). (7.13.1)
 (
(  ,
,  ,
,  ), (7.13)
), (7.13) то оно равносильно неравенству
 (
(  ,
,  ,
,  ). (7.13.1)
). (7.13.1)5. Если неравенство содержит несколько модулей, например, имеет вид
 , (
, (  ,
,  ,
,  ) , (7.14)
) , (7.14)
то применяем метод интервалов, следуя алгоритму:
 , (
, (  ,
,  ,
,  ) , (7.14)
) , (7.14) то применяем метод интервалов, следуя алгоритму:
1) находим нули функций, стоящих под знаком модуля, решая уравнения  и
и  ;
;
 и
и  ;
;2) наносим нули функций на область определения уравнения;
3) раскрываем модули на каждом промежутке;
4) решаем полученные неравенства;
5) производим отбор корней на каждом промежутке, оставляя корни, принадлежащие рассматриваемому промежутку.
Пример 1. Решите неравенство  .
.
 .
.Решение. Имеем неравенство вида 7.8, которое равносильно 7.8.1, следовательно, данное неравенство равносильно системе неравенств:



Поскольку второе неравенство системы выполняется при  , то первое неравенство системы решим методом интервалов на промежутке
, то первое неравенство системы решим методом интервалов на промежутке 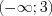 .
.
 , то первое неравенство системы решим методом интервалов на промежутке
, то первое неравенство системы решим методом интервалов на промежутке 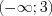 .
. Согласно рисунку 7.32 запишем решение системы неравенств, а, следовательно, и решение исходного неравенства:  .
.
 .
.
Ответ:  .
.
 .
. Пример 2. Решите неравенство  .
.
 .
.Решение. Имеем неравенство вида 7.9, которое равносильно 7.9.1, следовательно, данное неравенство равносильно совокупности неравенств:


Решим каждое неравенство совокупности:
1) поскольку левая часть неравенства  всегда положительна, а правая его часть всегда отрицательна и положительное число больше отрицательного, то неравенство не имеет решений;
всегда положительна, а правая его часть всегда отрицательна и положительное число больше отрицательного, то неравенство не имеет решений;
 всегда положительна, а правая его часть всегда отрицательна и положительное число больше отрицательного, то неравенство не имеет решений;
всегда положительна, а правая его часть всегда отрицательна и положительное число больше отрицательного, то неравенство не имеет решений;2) 


![\Leftrightarrow x\in (-\infty ;-31]\cup [33;+\infty) LaTeX formula: \Leftrightarrow x\in (-\infty ;-31]\cup [33;+\infty)](/uploads/formulas/d3cf23dca7a0cc450fb5efa7a31a8e4a4498e6a6.1.1.png) .
.



![\Leftrightarrow x\in (-\infty ;-31]\cup [33;+\infty) LaTeX formula: \Leftrightarrow x\in (-\infty ;-31]\cup [33;+\infty)](/uploads/formulas/d3cf23dca7a0cc450fb5efa7a31a8e4a4498e6a6.1.1.png) .
.Решением совокупности неравенств является решение второго неравенства совокупности.
Ответ: ![(-\infty ;-31]\cup [33;+\infty) LaTeX formula: (-\infty ;-31]\cup [33;+\infty)](/uploads/formulas/9bf5d05693825f1a708f5c1fc9c54c57a09eed96.1.1.png) .
.
![(-\infty ;-31]\cup [33;+\infty) LaTeX formula: (-\infty ;-31]\cup [33;+\infty)](/uploads/formulas/9bf5d05693825f1a708f5c1fc9c54c57a09eed96.1.1.png) .
.Пример 3. Найдите сумму решений системы неравенств 



![\Leftrightarrow x\in [-3,6; 3] LaTeX formula: \Leftrightarrow x\in [-3,6; 3]](/uploads/formulas/d21e569addc93751b251d3a817fe04fff55cf30b.1.1.png) ;
; 


![\Leftrightarrow x\in (-\infty;-3,6]\cup [3;+\infty) LaTeX formula: \Leftrightarrow x\in (-\infty;-3,6]\cup [3;+\infty)](/uploads/formulas/b2dc53bd5d7853b544c5cb1a9caea247c2c59bb6.1.1.png) .
.Очевидно, что решением системы неравенств являются числа –3,6 и 3, сумма которых равна –0,6.
Способ II. Заменим систему неравенств  равносильным уравнением
равносильным уравнением
 равносильным уравнением
равносильным уравнением 



Ответ:  .
.
 .
.Пример 4. Найдите наименьшее целое положительное решение неравенства  .
.
 .
.Решение. Поскольку  и
и  , то неравенство примет вид
, то неравенство примет вид  , решать которое будем методом интервалов.
, решать которое будем методом интервалов.
 и
и  , то неравенство примет вид
, то неравенство примет вид  , решать которое будем методом интервалов.
, решать которое будем методом интервалов.1. Рассмотрим функцию  .
.
 .
.2. 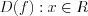 .
.
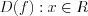 .
.3. Найдем нули функции, решая уравнение  . Получим
. Получим  , откуда
, откуда  или
или  , откуда
, откуда  ,
,  .
.
 . Получим
. Получим  , откуда
, откуда  или
или  , откуда
, откуда  ,
,  .
.4. Нанесем полученные числа на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.33).

5. Решением неравенства является объединение промежутков, на которых функция положительна:  .
.
 .
.Так как  , а
, а  , то число 1 является наименьшим целым положительным решением неравенства.
, то число 1 является наименьшим целым положительным решением неравенства.
 , а
, а  , то число 1 является наименьшим целым положительным решением неравенства.
, то число 1 является наименьшим целым положительным решением неравенства.Ответ: 1.
Пример 5. Найдите сумму квадратов целых решений неравенства  .
.
 .
.Разложим левую часть неравенства на множители, применяя формулу разности квадратов:
 ,
,  .
.Решим неравенство методом интервалов.
1. Рассмотрим функцию  .
.
 .
.2.  .
.
 .
.3. Найдем нули функции, решая совокупность уравнений:
1)  , откуда
, откуда  ;
;
 , откуда
, откуда  ;
;2)  , откуда
, откуда  ,
,  ,
,  и
и  .
.
 , откуда
, откуда  ,
,  ,
,  и
и  .
.4. Нанесем числа –1, 1, –3 и 3 на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.34).

5. Решением неравенства является объединение промежутков, на котором функция отрицательна:  .
.
 .
.Найдем сумму квадратов целых решений неравенства:  .
.
 .
.Ответ:  .
.
 .
.Всякое неравенство, содержащее переменную по знаком модуля, можно решить методом интервалов, но наиболее целесообразно применять этот метод в случае решения комбинированных неравенств.



