Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 (7.2.1)
(7.2.1)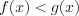 (
( ,
,  ,
,  ); (7.3.1)
); (7.3.1) (
( ,
,  ,
,  ); (7.4.1)
); (7.4.1) (
( ,
,  ,
,  ); (7.5.1)
); (7.5.1)


 .
. ![x^{2}+2x-15\geq 0\Leftrightarrow x\in (-\infty ;-5]\cup [3;+\infty ) LaTeX formula: x^{2}+2x-15\geq 0\Leftrightarrow x\in (-\infty ;-5]\cup [3;+\infty )](/uploads/formulas/934d56481f205e67b58847339ca0ef12809d68c5.1.1.png) (рис. 7.20).
(рис. 7.20).




 ,
,  ,
,  .
.


![\Leftrightarrow x\in (-\infty;0] LaTeX formula: \Leftrightarrow x\in (-\infty;0]](/uploads/formulas/ab963af3a81660aaf06c3cadb79c6433baac1492.1.1.png) (рис. 7.24).
(рис. 7.24).![x\in (-\infty;0]\cup (4,5;+\infty ) LaTeX formula: x\in (-\infty;0]\cup (4,5;+\infty )](/uploads/formulas/3d52a6fd935ddfac2d5708137746ec108d307ade.1.1.png) .
.



Иррациональными называют неравенства, содержащие переменную под знаком корня (радикала).
При решении иррациональных неравенств необходимо помнить:
а) если обе части неравенства на его области определения принимают только неотрицательные значения, то, возводя обе части в квадрат, (или в любую другую четную степень) и сохранив знак исходного неравенства, получим неравенство, равносильное данному (на области определения);
б) возводя обе части неравенства в одну и ту же нечетную степень, всегда получим неравенство, равносильное данному неравенству.
Методы решений неравенств
1. Рассмотрим неравенство вида  . (7.1)
. (7.1)
 . (7.1)
. (7.1)Так как выражение, стоящее под знаком радикала и правая часть неравенства не могут быть отрицательными, то, данное неравенство равносильно системе неравенств  (7.1.1)
(7.1.1)
 (7.1.1)
(7.1.1)2. Рассмотрим неравенство вида  . (7.2)
. (7.2)
 . (7.2)
. (7.2)Так как  может принимать как неотрицательные, так и отрицательные значения, то возможны два случая:
может принимать как неотрицательные, так и отрицательные значения, то возможны два случая:
 может принимать как неотрицательные, так и отрицательные значения, то возможны два случая:
может принимать как неотрицательные, так и отрицательные значения, то возможны два случая: 1) если  , то решаем систему неравенств
, то решаем систему неравенств
 , то решаем систему неравенств
, то решаем систему неравенств  (7.2.1)
(7.2.1)2) если  , то решаем систему неравенств
, то решаем систему неравенств  (7.2.2)
(7.2.2)
 , то решаем систему неравенств
, то решаем систему неравенств  (7.2.2)
(7.2.2)3. Неравенства с двумя радикалами:
1) неравенство  (
( ,
,  ,
,  ) (7.3)
) (7.3)
 (
( ,
,  ,
,  ) (7.3)
) (7.3)при  и
и  равносильно неравенству
равносильно неравенству
 и
и  равносильно неравенству
равносильно неравенству 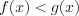 (
( ,
,  ,
,  ); (7.3.1)
); (7.3.1)2) неравенство  (
( ,
,  ,
,  ) (7.4)
) (7.4)
 (
( ,
,  ,
,  ) (7.4)
) (7.4)при  ,
,  и
и  равносильно неравенству
равносильно неравенству
 ,
,  и
и  равносильно неравенству
равносильно неравенству (
( ,
,  ,
,  ); (7.4.1)
); (7.4.1)3) неравенство  (
( ,
,  ,
,  ) (7.5)
) (7.5)
 (
( ,
,  ,
,  ) (7.5)
) (7.5)при ,
,  и
и  равносильно неравенству
равносильно неравенству
 ,
,  и
и  равносильно неравенству
равносильно неравенству (
( ,
,  ,
,  ); (7.5.1)
); (7.5.1)4) неравенство  (
(  ) (7.6)
) (7.6)
 (
(  ) (7.6)
) (7.6)при  равносильно системе неравенств
равносильно системе неравенств  и
и  ;
;
 равносильно системе неравенств
равносильно системе неравенств  и
и  ;
;5) неравенство  (
(  ) (7.7)
) (7.7)
 (
(  ) (7.7)
) (7.7)при  решений не имеет.
решений не имеет.
 решений не имеет.
решений не имеет.4. Иррациональные неравенства можно решить методом интервалов, следуя алгоритму:
1) записать неравенство в виде 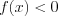 (
(  ,
,  ,
,  );
);
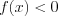 (
(  ,
,  ,
,  );
);2) найти область определения функции  ;
;
 ;
;3) найти нули функции, решая уравнение  ;
;
 ;
;4) нанести нули функции на ее область определения;
5) определить знак значений функции на любом промежутке;
6) определить знаки значений функции на остальных промежутках по правилу: при переходе через каждый корень уравнения  знак значений функции изменяется (при этом учитываем кратность корней);
знак значений функции изменяется (при этом учитываем кратность корней);
 знак значений функции изменяется (при этом учитываем кратность корней);
знак значений функции изменяется (при этом учитываем кратность корней);7) записать решение неравенства, учитывая его смысловой знак.
5. Использование монотонности функций.
Если функция  строго возрастает на некотором отрезке
строго возрастает на некотором отрезке ![\left [ a;b \right ] LaTeX formula: \left [ a;b \right ]](/uploads/formulas/f165e2ebf0de9dc9fdd510b5ddcf1bdd5e4de429.1.1.png) , а функция
, а функция  строго убывает на этом отрезке и
строго убывает на этом отрезке и  – корень уравнения
– корень уравнения  , то решением неравенства
, то решением неравенства 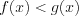 является промежуток
является промежуток  , а решением неравенства
, а решением неравенства 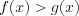 является промежуток
является промежуток ![(x_{0};b] LaTeX formula: (x_{0};b]](/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png) (рис. 7.19).
(рис. 7.19).
 строго возрастает на некотором отрезке
строго возрастает на некотором отрезке ![\left [ a;b \right ] LaTeX formula: \left [ a;b \right ]](/uploads/formulas/f165e2ebf0de9dc9fdd510b5ddcf1bdd5e4de429.1.1.png) , а функция
, а функция  строго убывает на этом отрезке и
строго убывает на этом отрезке и  – корень уравнения
– корень уравнения  , то решением неравенства
, то решением неравенства 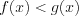 является промежуток
является промежуток  , а решением неравенства
, а решением неравенства 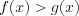 является промежуток
является промежуток ![(x_{0};b] LaTeX formula: (x_{0};b]](/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png) (рис. 7.19).
(рис. 7.19).
Аналогично решаются неравенства  и
и  , а также неравенства, где функция
, а также неравенства, где функция  имеет вид
имеет вид 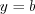 .
.
 и
и  , а также неравенства, где функция
, а также неравенства, где функция  имеет вид
имеет вид 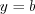 .
. Пример 1. Решите неравенство  .
.
 .
. Решение. Найдем область определения неравенства:


 .
.Поскольку левая часть неравенства представлена функцией, которая строго возрастает на области определения и  - корень уравнения
- корень уравнения  , то промежуток
, то промежуток  - решение данного неравенства.
- решение данного неравенства.
 - корень уравнения
- корень уравнения  , то промежуток
, то промежуток  - решение данного неравенства.
- решение данного неравенства.Ответ:  .
.
 .
.Пример 2. Решите неравенство  .
.
 .
.Решение. Так как выражение, стоящее под знаком радикала не может быть отрицательным, то запишем ОДЗ неравенства:
![x^{2}+2x-15\geq 0\Leftrightarrow x\in (-\infty ;-5]\cup [3;+\infty ) LaTeX formula: x^{2}+2x-15\geq 0\Leftrightarrow x\in (-\infty ;-5]\cup [3;+\infty )](/uploads/formulas/934d56481f205e67b58847339ca0ef12809d68c5.1.1.png) (рис. 7.20).
(рис. 7.20).
Поскольку левая часть неравенства неотрицательна, а правая всегда отрицательна на ОДЗ, то решением неравенства является любое число из промежутков ![(-\infty ;-5] LaTeX formula: (-\infty ;-5]](/uploads/formulas/2b7bdb48cd2e6ddfe851c4c77b41014faefd5e41.1.1.png) и
и  .
.
![(-\infty ;-5] LaTeX formula: (-\infty ;-5]](/uploads/formulas/2b7bdb48cd2e6ddfe851c4c77b41014faefd5e41.1.1.png) и
и  .
.Ответ: ![(-\infty ;-5]\cup [3;+\infty ) LaTeX formula: (-\infty ;-5]\cup [3;+\infty )](/uploads/formulas/265f6c091b0109d62313c31595f5a6b41a4d67e5.2.1.png) .
.
![(-\infty ;-5]\cup [3;+\infty ) LaTeX formula: (-\infty ;-5]\cup [3;+\infty )](/uploads/formulas/265f6c091b0109d62313c31595f5a6b41a4d67e5.2.1.png) .
.Пример 3. Найдите целые решения неравенства  .
.
 .
.Решение. Способ I. Запишем неравенство в виде 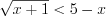 .
.
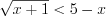 .
.Запишем систему ограничений: 


![x\in \left [ -1;5 \right ] LaTeX formula: x\in \left [ -1;5 \right ]](/uploads/formulas/10327e70a3952eeee5ffe1b71082ab5101926f09.1.1.png) .
.



![x\in \left [ -1;5 \right ] LaTeX formula: x\in \left [ -1;5 \right ]](/uploads/formulas/10327e70a3952eeee5ffe1b71082ab5101926f09.1.1.png) .
.Возводя обе части неравенства в квадрат, получим:  ,
,  ,
,  , откуда
, откуда  (рис. 7.21).
(рис. 7.21).
 ,
,  ,
,  , откуда
, откуда  (рис. 7.21).
(рис. 7.21). 
Запишем целые решения неравенства:  ;
;  ;
;  ;
;  .
.
 ;
;  ;
;  ;
;  .
.Способ II. Запишем неравенство в виде  и решим его методом интервалов.
и решим его методом интервалов.
 и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию  .
.
 .
.2.  .
.
 .
.3. Найдем нули функции, решая уравнение  при условии, что
при условии, что  .
.
 при условии, что
при условии, что  .
. Получим:  ,
,  , откуда
, откуда  ,
,  , причем
, причем  посторонний корень уравнения, так как он не удовлетворяет условию
посторонний корень уравнения, так как он не удовлетворяет условию  .
.
 ,
,  , откуда
, откуда  ,
,  , причем
, причем  посторонний корень уравнения, так как он не удовлетворяет условию
посторонний корень уравнения, так как он не удовлетворяет условию  .
.4. Нанесем число 3 на область определения функции и установим знаки ее значений на полученных промежутках (рис. 7.22).

5. Решением неравенства является промежуток, на котором функция  отрицательна:
отрицательна:  .
.
 отрицательна:
отрицательна:  .
. Ответ:  ;
;  ;
;  ;
;  .
.
 ;
;  ;
;  ;
;  .
.Пример 4. Найдите сумму целых решений неравенства  , удовлетворяющих условию
, удовлетворяющих условию ![\sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4} LaTeX formula: \sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4}](/uploads/formulas/3eb4bf50bd6ca7ee113f12a383c8df6ca34b6d33.1.1.png) .
.
 , удовлетворяющих условию
, удовлетворяющих условию ![\sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4} LaTeX formula: \sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4}](/uploads/formulas/3eb4bf50bd6ca7ee113f12a383c8df6ca34b6d33.1.1.png) .
.Решение. Способ I. Имеем неравенство 7.2, которое равносильно совокупности систем неравенств 7.2.1 и 7.2.2.
1. Если правая часть неравенства неотрицательна, то запишем систему ограничений: 

 (рис. 7.23).
(рис. 7.23).


 (рис. 7.23).
(рис. 7.23). 

Возведем обе части неравенства в квадрат и получим:
 ,
,  ,
,  .
.Учитывая систему ограничений, запишем:  .
.
 .
.2. Если правая часть неравенства отрицательна, то решим систему неравенств:



![\Leftrightarrow x\in (-\infty;0] LaTeX formula: \Leftrightarrow x\in (-\infty;0]](/uploads/formulas/ab963af3a81660aaf06c3cadb79c6433baac1492.1.1.png) (рис. 7.24).
(рис. 7.24).Решением исходного неравенства является объединение решений, полученных в первом и во втором случаях:
![x\in (-\infty;0]\cup (4,5;+\infty ) LaTeX formula: x\in (-\infty;0]\cup (4,5;+\infty )](/uploads/formulas/3d52a6fd935ddfac2d5708137746ec108d307ade.1.1.png) .
.Рассмотрим дополнительное ограничение ![\sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4} LaTeX formula: \sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4}](/uploads/formulas/3eb4bf50bd6ca7ee113f12a383c8df6ca34b6d33.1.1.png) и запишем его в виде
и запишем его в виде  . Это неравенство равносильно системе неравенств:
. Это неравенство равносильно системе неравенств: 


![\Leftrightarrow x\in \left [ -3;5 \right ] LaTeX formula: \Leftrightarrow x\in \left [ -3;5 \right ]](/uploads/formulas/94262ec205e52e817ac316ab59ee03a672a93754.1.1.png) .
.
![\sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4} LaTeX formula: \sqrt[4]{(1-x)^{4}}\leq (-\sqrt{2})^{4}](/uploads/formulas/3eb4bf50bd6ca7ee113f12a383c8df6ca34b6d33.1.1.png) и запишем его в виде
и запишем его в виде  . Это неравенство равносильно системе неравенств:
. Это неравенство равносильно системе неравенств: 


![\Leftrightarrow x\in \left [ -3;5 \right ] LaTeX formula: \Leftrightarrow x\in \left [ -3;5 \right ]](/uploads/formulas/94262ec205e52e817ac316ab59ee03a672a93754.1.1.png) .
.Запишем решение задачи (рис. 7.25): ![x\in \left [ -3;0 \right ]\cup (4,5;5] LaTeX formula: x\in \left [ -3;0 \right ]\cup (4,5;5]](/uploads/formulas/ede41c48ea36790e703fe232472dd00d311d93c3.1.1.png) .
.
![x\in \left [ -3;0 \right ]\cup (4,5;5] LaTeX formula: x\in \left [ -3;0 \right ]\cup (4,5;5]](/uploads/formulas/ede41c48ea36790e703fe232472dd00d311d93c3.1.1.png) .
. 
Найдем сумму целых решений задачи:  .
.
 .
.Способ II. Запишем неравенство в виде  и решим его методом интервалов.
и решим его методом интервалов.
 и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию  .
.
 .
.2.  . Поскольку решения неравенства должны удовлетворять условию
. Поскольку решения неравенства должны удовлетворять условию ![\left | x-1 \right |\leq 4\Leftrightarrow x\in \left [ -3;5 \right ] LaTeX formula: \left | x-1 \right |\leq 4\Leftrightarrow x\in \left [ -3;5 \right ]](/uploads/formulas/59f912a500eecae2308a128881e4f36799124989.1.1.png) , то решим неравенство
, то решим неравенство  на отрезке
на отрезке ![\left [ -3;5 \right ] LaTeX formula: \left [ -3;5 \right ]](/uploads/formulas/6a7d2bc85c2cc3e61b66d2876a19808e972ec703.1.1.png) и согласно рисунку 7.26 запишем: .
и согласно рисунку 7.26 запишем: .
 . Поскольку решения неравенства должны удовлетворять условию
. Поскольку решения неравенства должны удовлетворять условию ![\left | x-1 \right |\leq 4\Leftrightarrow x\in \left [ -3;5 \right ] LaTeX formula: \left | x-1 \right |\leq 4\Leftrightarrow x\in \left [ -3;5 \right ]](/uploads/formulas/59f912a500eecae2308a128881e4f36799124989.1.1.png) , то решим неравенство
, то решим неравенство  на отрезке
на отрезке ![\left [ -3;5 \right ] LaTeX formula: \left [ -3;5 \right ]](/uploads/formulas/6a7d2bc85c2cc3e61b66d2876a19808e972ec703.1.1.png) и согласно рисунку 7.26 запишем: .
и согласно рисунку 7.26 запишем: .

3. Найдем нули функции, решая уравнение  , при условии, что
, при условии, что  . Получим:
. Получим:  , откуда
, откуда  .
.
 , при условии, что
, при условии, что  . Получим:
. Получим:  , откуда
, откуда  .
.4. Нанесем число  на область определения функции и определим знаки ее значений на полученных промежутках (рис. 7.27).
на область определения функции и определим знаки ее значений на полученных промежутках (рис. 7.27).
 на область определения функции и определим знаки ее значений на полученных промежутках (рис. 7.27).
на область определения функции и определим знаки ее значений на полученных промежутках (рис. 7.27).5. Решением неравенства является объединение промежутков, на которых функция положительна: ![x\in \left [ -3;0 \right ]\cup \left ( 4,5;5 \right ] LaTeX formula: x\in \left [ -3;0 \right ]\cup \left ( 4,5;5 \right ]](/uploads/formulas/dcd955b490745ac5701c7fa80e3d6aa45d8f3a09.1.1.png) .
.
![x\in \left [ -3;0 \right ]\cup \left ( 4,5;5 \right ] LaTeX formula: x\in \left [ -3;0 \right ]\cup \left ( 4,5;5 \right ]](/uploads/formulas/dcd955b490745ac5701c7fa80e3d6aa45d8f3a09.1.1.png) .
.Этим промежуткам принадлежит  целых решений неравенства, сумма которых равна
целых решений неравенства, сумма которых равна  .
.
 целых решений неравенства, сумма которых равна
целых решений неравенства, сумма которых равна  .
.Ответ:  .
.
 .
.Пример 5. Найдите среднее арифметическое целых решений неравенства ![\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}> 0 LaTeX formula: \sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}> 0](/uploads/formulas/a3d7f24b9d0db5872d0734a9ee36cc8f2c3c6541.1.1.png) .
.
![\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}> 0 LaTeX formula: \sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}> 0](/uploads/formulas/a3d7f24b9d0db5872d0734a9ee36cc8f2c3c6541.1.1.png) .
.Решение. Решим неравенство методом интервалов.
1. Рассмотрим функцию ![f(x)=\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x} LaTeX formula: f(x)=\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}](/uploads/formulas/ac49130e12155694290c20579a61a1e07ecca3bc.1.1.png) .
.
![f(x)=\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x} LaTeX formula: f(x)=\sqrt[11]{-x^{2}+5x+6} \cdot \sqrt[10]{4-x}](/uploads/formulas/ac49130e12155694290c20579a61a1e07ecca3bc.1.1.png) .
.2.  ,
,  .
.
 ,
,  .
.3. Найдем нули функции, решая уравнения  и
и  . Получим:
. Получим:  ,
,  ,
,  .
.
 и
и  . Получим:
. Получим:  ,
,  ,
,  .
.4. Нанесем числа –1 и 4 на область определения функции и установим знаки ее значений на полученных промежутках (рис. 7.28).

5. Согласно рисунку 7.28 решением неравенства является интервал  , на котором функция положительна.
, на котором функция положительна.
 , на котором функция положительна.
, на котором функция положительна. Найдем среднее арифметическое целых решений неравенства:  .
.
 .
.Ответ:  .
.
 .
.Всякое иррациональное неравенство можно решить методом интервалов, но наиболее целесообразно применять этот метод в случае решения неравенств вида 7.2 и комбинированных неравенств.

