Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Неравенство вида 
(>; ≤; ≥) называют линейным.
(>; ≤; ≥) называют линейным. Чтобы решить линейное неравенство необходимо привести его к виду 
(>, ≤, ≥).
Для этого слагаемые, содержащие переменную, переносят в одну часть неравенства, а слагаемые, не содержащие переменную – в другую.
Разделив обе части неравенства на коэффициент при переменной (если он отличен от нуля), получают решение неравенства.
(>, ≤, ≥). Для этого слагаемые, содержащие переменную, переносят в одну часть неравенства, а слагаемые, не содержащие переменную – в другую.
Разделив обе части неравенства на коэффициент при переменной (если он отличен от нуля), получают решение неравенства.
При этом возможны следующие случаи.
1. Если 
и 
, то 
– решение неравенства 
.
и , то – решение неравенства .2. Если 
и , то 
– решение неравенства 
.
и , то – решение неравенства .3. Если 
и 
, то неравенство примет вид 
или 
. Поскольку полученное числовое неравенство не верное, то неравенство решений не имеет. Записывают: решений нет. Можно записать иначе: 
.
и , то неравенство примет вид или . Поскольку полученное числовое неравенство не верное, то неравенство решений не имеет. Записывают: решений нет. Можно записать иначе: .4. Если 
и 
, то неравенство примет вид 
или 
. Поскольку полученное числовое неравенство верное, то неравенство имеет бесконечное множество решений. Записывают: 
.
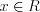и , то неравенство примет вид или . Поскольку полученное числовое неравенство верное, то неравенство имеет бесконечное множество решений. Записывают: 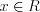.Пример 1. Найдите середину интервала, являющегося решением системы неравенств
Решение. Решим каждое неравенство системы:
1) 
;
;2) 
, поскольку 
.
, поскольку . Найдем решение данной системы неравенств.
Согласно рисунку 7.7 запишем:
.
Согласно рисунку 7.7 запишем:
.
Найдем середину интервала: 
.
.Ответ: 0,05.
Пример 2. Найдите наибольшее целое решение совокупности неравенств 
Решение. Найдем решение каждого неравенства совокупности, выполнив равносильные преобразования неравенств:
1) 
;
;2) 
.
.Поскольку решение второго неравенства содержит решение первого неравенства, то решением данной совокупности неравенств является промежуток 
, а число –1 является наибольшим целым решением этой совокупности неравенств.
, а число –1 является наибольшим целым решением этой совокупности неравенств.Ответ: –1.
Сравните решения неравенств:
1) 
;
;2) ;
;3) 
;
;4) 
;
;5) 
;
;6) 
.
.