Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
, 
, 
, 
, 
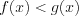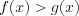Неравенством с одной переменной называют каждое из выражений вида:
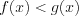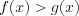, , , , где знаки 
, 
, 
, 
означают соответственно меньше, больше, меньше или равно, больше или равно.
, , , означают соответственно меньше, больше, меньше или равно, больше или равно. Н а п р и м е р, 
, 
, 
, 
, 
– примеры неравенств с одной переменной.
, , , , – примеры неравенств с одной переменной.Решением неравенства называют значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – значит найти множество всех его решений или доказать, что неравенство не имеет решений.
Областью определения (областью допустимых значений) неравенства 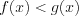называют общую часть областей определения функций 
и 
.
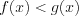называют общую часть областей определения функций и .Равносильные неравенства
Два неравенства называют равносильными, если множества их решений совпадают или оба неравенства не имеют решений.
Н а п р и м е р:
1) неравенства
и 
равносильны, так как оба неравенства выполняются на множестве действительных чисел;
2) неравенства
и 
равносильны, так как оба неравенства не имеют решений;
1) неравенства
и равносильны, так как оба неравенства выполняются на множестве действительных чисел; 2) неравенства
и равносильны, так как оба неравенства не имеют решений; Решая неравенство, как правило, его заменяют более простым, но равносильным ему неравенством. Такие замены осуществляют на основании следующих утверждений:
1. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получим неравенство, равносильное данному неравенству.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число или на одну и ту же функцию, положительную на области определения неравенства, то получим неравенство, равносильное данному неравенству.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число или на одну и ту же функцию, отрицательную на области определения неравенства, изменив при этом смысловой знак неравенства, то получим неравенство, равносильное данному.
4. Неравенства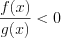 
и 
, а также неравенства 
и 
равносильны.
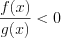и , а также неравенства и равносильны. 5. Неравенства 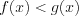и 
равносильны для всех 
при условии, что значения выражений 
и 
неотрицательные.
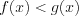и равносильны для всех при условии, что значения выражений и неотрицательные. 6. Неравенства 
и 
равносильны для всех 
.
и равносильны для всех . 7. Неравенства ![LaTeX formula: \sqrt[2n+1]{f(x)}< \sqrt[2n+1]{g(x)}](/uploads/formulas/fba645ad1ebd71ce03c560c56e25ab36b08ec1bc.1.1.png "\sqrt[2n+1]{f(x)}< \sqrt[2n+1]{g(x)}")
и 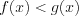равносильны для всех .
и 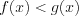равносильны для всех . Системы и совокупности неравенств с одной переменной
Рассмотрим два неравенства 
и 
.
и . Систему двух неравенств записывают в виде: 
Совокупность неравенств записывают в виде: 
Чтобы решить систему неравенств, необходимо найти множества решений каждого неравенства системы, тогда общая часть (пересечение) этих множеств и будет решением системы.
Чтобы решить совокупность неравенств, необходимо найти множества решений каждого неравенства совокупности, тогда объединение этих множеств и будет решением совокупности.
Метод интервалов
Метод интервалов основан на следующем свойстве двучлена: если отметить на координатной оси 
число 
(рис. 7.1), то для любого 
, находящегося справа от точки 
, двучлен 
положителен, а слева от точки 
он отрицателен.
число (рис. 7.1), то для любого , находящегося справа от точки , двучлен положителен, а слева от точки он отрицателен. Рассмотрим дробно-рациональную функцию 
где: 
.
где: . Если 
, то каждый из сомножителей 
, 
, 
, 
положителен, и, следовательно, на промежутке 
имеем 
(рис. 7.2).
Если
, то множитель 
, а остальные сомножители по-прежнему положительны. Значит, на промежутке 
имеем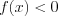 
. Однако при разложении левой части неравенства могут встретиться одинаковые множители.
, то каждый из сомножителей , , , положителен, и, следовательно, на промежутке имеем (рис. 7.2). Если
, то множитель , а остальные сомножители по-прежнему положительны. Значит, на промежутке имеем 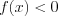. Однако при разложении левой части неравенства могут встретиться одинаковые множители. Число 
называют кратностью корня 
многочлена 
, а число – k-кратным корнем этого многочлена.
называют кратностью корня многочлена , а число – k-кратным корнем этого многочлена. В процессе решения неравенств методом интервалов для удобства корни четной кратности будем наносить на координатную прямую дважды, а нечетной кратности – один раз. При переходе через корень четной кратности знаки значений функции не изменятся, а при переходе через корень нечетной кратности – изменятся.
При решении неравенств вида 
и 
корни числителя будем отмечать на координатной прямой «зачерненными» кружочками, а корни знаменателя – «пустыми», так как множество решений неравенства не должно содержать корней многочлена .
и корни числителя будем отмечать на координатной прямой «зачерненными» кружочками, а корни знаменателя – «пустыми», так как множество решений неравенства не должно содержать корней многочлена . Пример 1. Найдите область определения неравенства 
.
.Решение. Областью определения функции 
является промежуток 
.
Областью определения функции
является промежуток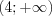 
.
Следовательно, областью определения данного неравенства является промежуток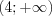
.
является промежуток . Областью определения функции
является промежуток 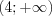. Следовательно, областью определения данного неравенства является промежуток
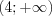.Ответ: .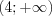
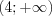.Пример 2. Решите систему неравенств 
и совокупность неравенств 
и совокупность неравенств Решение. Решением системы неравенств 
является промежуток 
(рис. 7.3).
является промежуток (рис. 7.3).Решением совокупности неравенств 
являются промежутки 
и 
(рис. 7.4).
являются промежутки и (рис. 7.4). Ответ: 
; 
.
; .Пример 3. Решите неравенства 
и 
.
и .Решение. Решение неравенства показано на рисунке 7.5: 
.
показано на рисунке 7.5: . Решение неравенства показано на рисунке 7.6: ![LaTeX formula: x\in (-\infty ;2 )\cup \left [ 3;6 \right ]](/uploads/formulas/0bc6e490f8a5b35547f8edf360065176b4e91367.1.1.png "x\in (-\infty ;2 )\cup \left [ 3;6 \right ]")
.
показано на рисунке 7.6: . Ответ: 
; ![LaTeX formula: (-\infty ;2 )\cup \left [ 3;6 \right ]](/uploads/formulas/8de12b9847e5e6750afd8481616bbefd39b86c81.1.1.png "(-\infty ;2 )\cup \left [ 3;6 \right ]")
.
; .Наряду с алгебраическим подходом к решению неравенств можно использовать также и функциональный подход.
Приведем алгоритм решения методом интервалов неравенства вида 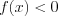( , , ), где функция 
может быть произвольной (рациональной, иррациональной, показательной, логарифмической, тригонометрической и т. д.):
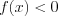( , , ), где функция может быть произвольной (рациональной, иррациональной, показательной, логарифмической, тригонометрической и т. д.):1) запишем функцию ;
;2) найдем область определения функции;
3) найдем нули функции, решая уравнение 
;
;4) нанесем нули функции на ее область определения;
5) определим знаки значений функции на одном из полученных промежутков;
6) определим знаки значений функции на остальных промежутках по правилу: при переходе через каждый нуль функции знаки значений функции изменяются (учитываем кратность нулей);
7) запишем решение неравенства, учитывая его смысловой знак.