Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Пример 1. Найдите шестой член геометрической прогрессии с положительным членами, если ее третий член равен
Найдем знаменатель прогрессии:
Найдем шестой член прогрессии:
Ответ:
Пример 2. Найдите знаменатель геометрической прогрессии, члены которой поочередно меняют знак, если сумма первых шести членов равна
Разделим первое уравнение системы на второе:
1. Знаменатель геометрической прогрессии q можно найти по формуле:
Возведем обе части исходного равенства дважды в квадрат:
Геометрической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, умноженному на одно и то же число  . Число
. Число  называют знаменателем геометрической прогрессии.Н а п р и м е р,числовая последовательность
называют знаменателем геометрической прогрессии.Н а п р и м е р,числовая последовательность  … является геометрической прогрессией, первый член которой равен
… является геометрической прогрессией, первый член которой равен 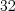 , а знаменатель ее равен
, а знаменатель ее равен  .Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и разность.Если
.Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и разность.Если  – первый член прогрессии
– первый член прогрессии  ,
,  – знаменатель прогрессии
– знаменатель прогрессии  , а
, а  – количество членов прогрессии, то справедливы следующие формулы.Формула
– количество членов прогрессии, то справедливы следующие формулы.Формула  -го члена:
-го члена: . (6.4)Формула суммы
. (6.4)Формула суммы  первых членов:
первых членов: . (6.5)Свойство
. (6.5)Свойство  –го члена
–го члена . (6.6)Если
. (6.6)Если  , то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле:
, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле: . (6.7)
. (6.7)
 .
.  называют знаменателем геометрической прогрессии.
называют знаменателем геометрической прогрессии. … является геометрической прогрессией, первый член которой равен
… является геометрической прогрессией, первый член которой равен 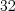 , а знаменатель ее равен
, а знаменатель ее равен  .
. – первый член прогрессии
– первый член прогрессии  ,
,  – знаменатель прогрессии
– знаменатель прогрессии  , а
, а  – количество членов прогрессии, то справедливы следующие формулы.
– количество членов прогрессии, то справедливы следующие формулы. -го члена:
-го члена: . (6.4)
. (6.4) первых членов:
первых членов: . (6.5)
. (6.5) –го члена
–го члена . (6.6)
. (6.6) , то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле:
, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле: . (6.7)
. (6.7)Пример 1. Найдите шестой член геометрической прогрессии с положительным членами, если ее третий член равен  , а пятый член равен
, а пятый член равен  .
.
Решение. Согласно свойству 6.6 запишем:
 .
.
Найдем знаменатель прогрессии:
 .
.
Найдем шестой член прогрессии:
 .
.
Ответ:  .
.
Пример 2. Найдите знаменатель геометрической прогрессии, члены которой поочередно меняют знак, если сумма первых шести членов равна  , а сумма первого и четвертого члена равна
, а сумма первого и четвертого члена равна  .
.
Решение. Условию задачи соответствует система уравнений 
Применяя формулы 6.4 и 6.5, запишем:
Разделим первое уравнение системы на второе:
 откуда
откуда  .
.
Найдем первый член прогрессии, подставляя значения  в уравнение
в уравнение  :
:
если  , то
, то  ;
;
если  , то
, то  .
.
Так как согласно условию задачи члены заданной геометрической прогрессии поочередно меняют знак, то знаменатель прогрессии равен 
 .
.
Ответ: 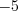 .
.
Пример 3. Сумма бесконечной убывающей геометрической прогрессии равна  , а сумма квадратов членов этой же прогрессии равна
, а сумма квадратов членов этой же прогрессии равна  . Найдите четвертый член прогрессии.
. Найдите четвертый член прогрессии.
Решение. Рассмотрим бесконечную убывающую геометрическую прогрессию с первым членом  и знаменателем
и знаменателем  :
:

Согласно формуле 6.7 запишем:
 ,
,  .
.
Рассмотрим бесконечную убывающую геометрическую прогрессию  с первым членом
с первым членом  и знаменателем
и знаменателем  .
.
Согласно формуле 6.7 запишем:
 .
.
Зная, что  получим:
получим:

 .
.
Тогда  .
.
По формуле 6.4 найдем четвертый член этой прогрессии:
 .
.
Ответ:  .
.
Пример 4. Найдите  , если
, если 
Решение. Запишем


Рассмотрим показатели степеней:
1)  – сумма бесконечно убывающей геометрической прогрессии, у которой
– сумма бесконечно убывающей геометрической прогрессии, у которой  и
и  . Тогда по формуле 6.7
. Тогда по формуле 6.7 
2)  – сумма бесконечно убывающей геометрической прогрессии, у которой
– сумма бесконечно убывающей геометрической прогрессии, у которой  и
и  . Тогда по формуле 6.7
. Тогда по формуле 6.7 
Получим  откуда
откуда  .
.
Ответ:  .
.
Пример 5. Найдите сумму корней уравнения  , если
, если  .
.
Решение. Прибавляя к обеим частям уравнения число  , запишем:
, запишем:
 .
.
Поскольку в левой части уравнения записана сумма бесконечной убывающей геометрической прогрессии с первым членом  и знаменателем
и знаменателем  , то согласно формуле 6.7 получим:
, то согласно формуле 6.7 получим:
 откуда
откуда  .
.
Так как оба корня удовлетворяют условию  , то найдем их сумму:
, то найдем их сумму:  .
.
Ответ:  .
.
1. Знаменатель геометрической прогрессии q можно найти по формуле:  .
.
2. Различайте формулы:
1)  – сумма
– сумма  первых членов любой геометрической прогрессии;
первых членов любой геометрической прогрессии;
2)  – сумма всех членов бесконечной убывающей геометрической прогрессии.
– сумма всех членов бесконечной убывающей геометрической прогрессии.
3. Пример 4 можно решить иначе:










 .
.