Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Пример 1. Сумма семнадцати первых членов арифметической прогрессии равна
Та как по формуле 6.1
Поскольку прогрессия содержит
Ответ:
Найдем второй член прогрессии:
Согласно формуле 6.1
Рассмотрим члены прогрессии с нечетными номерами:
Поскольку
1. Разность прогрессии можно найти по формуле:
2. Сумма членов арифметической прогрессии с
Арифметической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, увеличенному на одно и то же число  .
.
 .
. Число  называют разностью арифметической прогрессии.Если
называют разностью арифметической прогрессии.Если  , то арифметическая прогрессия является возрастающей числовой последовательностью, а если
, то арифметическая прогрессия является возрастающей числовой последовательностью, а если  , то – убывающей числовой последовательностью. Н а п р и м е р, числовая последовательность
, то – убывающей числовой последовательностью. Н а п р и м е р, числовая последовательность  … является убывающей арифметической прогрессией, первый член которой равен
… является убывающей арифметической прогрессией, первый член которой равен  , а ее разность равна
, а ее разность равна 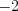 .Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность.
.Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность.
Если  – первый член прогрессии,
– первый член прогрессии,  – разность прогрессии, а
– разность прогрессии, а  – количество членов прогрессии, то справедливы следующие формулы.1. Формула
– количество членов прогрессии, то справедливы следующие формулы.1. Формула  -го члена:
-го члена: . (6.1)2. Формулы суммы
. (6.1)2. Формулы суммы  первых членов:
первых членов: (6.2)
(6.2)  . (6.2.1)3. Свойство
. (6.2.1)3. Свойство  -го члена:
-го члена: . (6.3)
. (6.3)
 называют разностью арифметической прогрессии.
называют разностью арифметической прогрессии. , то арифметическая прогрессия является возрастающей числовой последовательностью, а если
, то арифметическая прогрессия является возрастающей числовой последовательностью, а если  , то – убывающей числовой последовательностью.
, то – убывающей числовой последовательностью.  … является убывающей арифметической прогрессией, первый член которой равен
… является убывающей арифметической прогрессией, первый член которой равен  , а ее разность равна
, а ее разность равна 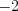 .
.Если
 – первый член прогрессии,
– первый член прогрессии,  – разность прогрессии, а
– разность прогрессии, а  – количество членов прогрессии, то справедливы следующие формулы.
– количество членов прогрессии, то справедливы следующие формулы. -го члена:
-го члена: . (6.1)
. (6.1) первых членов:
первых членов: (6.2)
(6.2)  . (6.2.1)
. (6.2.1) -го члена:
-го члена: . (6.3)
. (6.3)Пример 1. Сумма семнадцати первых членов арифметической прогрессии равна  . Найдите девятый член этой прогрессии.
. Найдите девятый член этой прогрессии.
Решение. Согласно формуле 6.2 Запишем сумму  первых членов прогрессии:
первых членов прогрессии:
 .
.
Так как  , то
, то  , откуда
, откуда
 и
и  .
.
Та как по формуле 6.1  , то
, то  .
.
Ответ:  .
.
Пример 2. Арифметическая прогрессия содержит  членов. Первый член прогрессии равен
членов. Первый член прогрессии равен  , разность ее равна
, разность ее равна  . Сколько членов этой прогрессии нужно взять, чтобы их сумма была равна
. Сколько членов этой прогрессии нужно взять, чтобы их сумма была равна  ?
?
Решение. Согласно условию задачи:
 ,
,  ,
,  .
.
С учетом формулы 6.2 запишем уравнение:
 , откуда
, откуда

 .
.
Поскольку прогрессия содержит  членов, то
членов, то  .
.
Ответ:  .
.
Пример 3. Двадцать пять чисел, первое из которых равно единице, а каждое следующее на 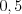 больше предыдущего, в порядке возрастания расположены в двух таблицах. Сумма чисел первой таблицы равна
больше предыдущего, в порядке возрастания расположены в двух таблицах. Сумма чисел первой таблицы равна  . Сколько чисел содержится во второй таблице?
. Сколько чисел содержится во второй таблице?
Решение. Согласно условию задачи запишем:  ,
,  .
.
Если в первой таблице  чисел, то
чисел, то  .
.
Подставляя значения  ,
,  и
и  в формулу 6.2 , получим:
в формулу 6.2 , получим:


 откуда
откуда  ,
,  .
.
Поскольку  – посторонний корень уравнения, то
– посторонний корень уравнения, то 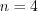 и, следовательно, в первой таблице
и, следовательно, в первой таблице  числа. Так как имеется
числа. Так как имеется  чисел, то вторая таблица содержит
чисел, то вторая таблица содержит  число.
число.
Ответ:  .
.
Пример 4. При делении тринадцатого члена арифметической прогрессии на третий член в частном получается  , а при делении восемнадцатого члена на седьмой член в частном получается
, а при делении восемнадцатого члена на седьмой член в частном получается  и в остатке
и в остатке  . Определите второй член прогрессии.
. Определите второй член прогрессии.
Решение. Согласно условию задачи запишем систему уравнений:

Применяя формулу 6.1 , получим:
 и
и  .
.
Система уравнений примет вид:
Найдем второй член прогрессии:
 .
.
Ответ:  .
.
Пример 5. В арифметической прогрессии  членов. Сумма членов с четными номерами равна
членов. Сумма членов с четными номерами равна  , а сумма членов с нечетными номерами равна
, а сумма членов с нечетными номерами равна  . Чему равна разность этой прогрессии?
. Чему равна разность этой прогрессии?
Решение. Рассмотрим члены прогрессии с четными номерами:  .
.
Согласно формуле 6.2.1 получим:

 .
.
Согласно формуле 6.1  и
и  .
.
Тогда  ,
,  .
.
Рассмотрим члены прогрессии с нечетными номерами:  .
.
Выполняя аналогичные действия, получим:




Вычитая из уравнения  уравнение
уравнение  , найдем разность прогрессии:
, найдем разность прогрессии:
 .
.
Ответ:  .
.
Пример 6. Найдите сумму всех четных натуральных двузначных чисел, которые при делении на  дают в остатке
дают в остатке  .
.
Решение. Найдем наименьшее четное натуральное двузначное число, которое при делении на  дает в остатке
дает в остатке  Это
Это 
Найдем наибольшее четное двузначное натуральное число, которое при делении на  дает в остатке
дает в остатке  . Для этого разделим
. Для этого разделим  на
на  .
.
Поскольку  , то
, то  .
.
Очевидно, что множество рассматриваемых чисел образует арифметическую прогрессию, у которой  и
и  .
.
Найдем число членов этой прогрессии.
Согласно формуле 6.1 получим:
 , откуда
, откуда  и
и 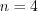 .
.
В соответствии с формулой 6.2.1 запишем:
 ,
,  .
.
Ответ:  .
.
Пример 7. Найдите сумму с четвертого члена по седьмой член арифметической прогрессии, если ее пятый член равен  , а седьмой член равен
, а седьмой член равен  .
.
 , а седьмой член равен
, а седьмой член равен  .
.Найдем разность прогрессии:  .
.
 .
.Найдем четвертый член прогрессии:  .
.
 .
.Тогда  .
.
 .
.Ответ:  .
.
 .
.




 .
.
 .
.