Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты



 ,
,  ,
,  ,
,  , откуда
, откуда  км/ч.
км/ч.
Ответ: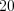 км/ч.
км/ч.



Пропорции
Две взаимно зависимые величины называются пропорциональными, если отношение их значений остается неизменным.
Неизменное отношение пропорциональных величин называют коэффициентом пропорциональности и обозначают :
:
 .
.
Основное свойство пропорции:
Неизменное отношение пропорциональных величин называют коэффициентом пропорциональности и обозначают
 :
: .
.Основное свойство пропорции:
если 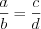 , то
, то  .
.
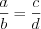 , то
, то  .
.Процентом числа называют одну сотую часть этого числа:  % от числа
% от числа  равен
равен  .
.
 % от числа
% от числа  равен
равен  .
.Задачи на проценты
1. Нахождение процента от числа:
 % от числа
% от числа  равны
равны  .
.
 % от числа
% от числа  равны
равны  .
. 2. Нахождение числа по его проценту:
если % от некоторого числа равны
% от некоторого числа равны  , то это число равно
, то это число равно  .
.
если
 % от некоторого числа равны
% от некоторого числа равны  , то это число равно
, то это число равно  .
. 3. Нахождение процентного отношения чисел:
процентное отношение числа к числу
к числу  равно
равно  %.
%.
процентное отношение числа
 к числу
к числу  равно
равно  %.
%. Соотношения между натуральными числами
Рассмотрим запись чисел в десятичной позиционной системе счисления.
Так, например, если – цифра десятков,
– цифра десятков,  – цифра единиц, то запишем:
– цифра единиц, то запишем:
 .
.
Так, например, если
 – цифра десятков,
– цифра десятков,  – цифра единиц, то запишем:
– цифра единиц, то запишем:  .
. Аналогично запишем трехзначное число, у которого  – цифра сотен,
– цифра сотен,  – цифра десятков,
– цифра десятков,  – цифра единиц:
– цифра единиц:
 .
.
 – цифра сотен,
– цифра сотен,  – цифра десятков,
– цифра десятков,  – цифра единиц:
– цифра единиц: .
.Задачи на движение
Уравнения, которые необходимо составить на основании условий задач на движение, содержат следующие величины: расстояние  , скорость
, скорость  , время
, время  .
.
Связь между этими величинами выражается формулой: .
.
 , скорость
, скорость  , время
, время  .
. Связь между этими величинами выражается формулой:
 .
.Если тело движется по течению реки, то его скорость слагается из собственной скорости и скорости течения реки:
 по теч. =
по теч. =  с. +
с. +  теч.
теч.
 по теч. =
по теч. =  с. +
с. +  теч.
теч.Если тело движется против течения реки, то  пр. теч. =
пр. теч. =  c. –
c. – теч.
теч.
 пр. теч. =
пр. теч. =  c. –
c. – теч.
теч.Если речь идет о движении плота, то его скорость равна скорости движения реки.
Задачи на работу
Уравнения, которые необходимо составить на основании условий задач на работу, содержат следующие величины: работу  , скорость выполнения работы (производительность)
, скорость выполнения работы (производительность)  , время выполнения работы
, время выполнения работы  .
.
Эти величины связаны формулой: .
.
 , скорость выполнения работы (производительность)
, скорость выполнения работы (производительность)  , время выполнения работы
, время выполнения работы  .
. Эти величины связаны формулой:
 .
.Смеси, сплавы
Задачи на смеси и сплавы удобно решать, учитывая пропорциональную зависимость между величинами. При помощи пропорции они сводятся к одной схеме решения.
Пример 1. На экзамене по математике  % поступающих не решили ни одной задачи,
% поступающих не решили ни одной задачи,  человек решили задачи с ошибками, а число решивших все задачи верно, относится к числу не решивших вовсе как
человек решили задачи с ошибками, а число решивших все задачи верно, относится к числу не решивших вовсе как  . Определите, сколько человек присутствовало на экзамене. Укажите наименьшее значение параметра
. Определите, сколько человек присутствовало на экзамене. Укажите наименьшее значение параметра  .
.
Решение. Запишем условие задачи:
 % поступающих не решили ни одной задачи,
% поступающих не решили ни одной задачи,  человек решили задачи с ошибками, а число решивших все задачи верно, относится к числу не решивших вовсе как
человек решили задачи с ошибками, а число решивших все задачи верно, относится к числу не решивших вовсе как  . Определите, сколько человек присутствовало на экзамене. Укажите наименьшее значение параметра
. Определите, сколько человек присутствовало на экзамене. Укажите наименьшее значение параметра  .
. Решение. Запишем условие задачи:

Пояснения к условию задачи:
а) если экзаменовалось человек, то
человек, то  % от
% от  равны
равны  ;
;
б) если число решивших верно, относится к числу не решивших вовсе как , то, вводя коэффициент пропорциональности
, то, вводя коэффициент пропорциональности  , получим: не решили ни одной задачи
, получим: не решили ни одной задачи  человек, решили верно все задачи
человек, решили верно все задачи  человек.
человек.
Согласно условию задачи составим и решим систему уравнений:



Следовательно, на экзамене присутствовало человек.
человек.
Поскольку согласно условию задачи целое положительное число, то
целое положительное число, то  при
при  и наименьшее значение
и наименьшее значение  равно
равно  .
.
Ответ:
а) если экзаменовалось
 человек, то
человек, то  % от
% от  равны
равны  ;
; б) если число решивших верно, относится к числу не решивших вовсе как
 , то, вводя коэффициент пропорциональности
, то, вводя коэффициент пропорциональности  , получим: не решили ни одной задачи
, получим: не решили ни одной задачи  человек, решили верно все задачи
человек, решили верно все задачи  человек.
человек. Согласно условию задачи составим и решим систему уравнений:



Следовательно, на экзамене присутствовало
 человек.
человек.Поскольку согласно условию задачи
 целое положительное число, то
целое положительное число, то  при
при  и наименьшее значение
и наименьшее значение  равно
равно  .
. Ответ:

Пример 2. Цену товара сначала снизили на 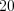 %, затем новую цену снизили еще на
%, затем новую цену снизили еще на  % и, наконец, произвели снижение еще на
% и, наконец, произвели снижение еще на  %. На сколько процентов необходимо повысить последнюю цену товара, чтобы получить его первоначальную цену?
%. На сколько процентов необходимо повысить последнюю цену товара, чтобы получить его первоначальную цену?
Решение. Пусть первоначальная цена товара была ден. ед.
ден. ед.
Согласно условию задачи составим и решим пропорции:
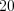 %, затем новую цену снизили еще на
%, затем новую цену снизили еще на  % и, наконец, произвели снижение еще на
% и, наконец, произвели снижение еще на  %. На сколько процентов необходимо повысить последнюю цену товара, чтобы получить его первоначальную цену?
%. На сколько процентов необходимо повысить последнюю цену товара, чтобы получить его первоначальную цену? Решение. Пусть первоначальная цена товара была
 ден. ед.
ден. ед. Согласно условию задачи составим и решим пропорции:
1) первоначальная цена  –
–  %,
%,
цена после снижения
снижения  – 80%,
– 80%,
откуда (ден. ед.);
(ден. ед.);
 –
–  %,
%, цена после
 снижения
снижения  – 80%,
– 80%, откуда
 (ден. ед.);
(ден. ед.);2) цена после  снижения
снижения  – 100%,
– 100%,
цена после снижения
снижения  – 85%,
– 85%,
 снижения
снижения  – 100%,
– 100%, цена после
 снижения
снижения  – 85%,
– 85%,откуда  (ден. ед.);
(ден. ед.);
 (ден. ед.);
(ден. ед.);3) цена после  снижения
снижения  – 100%,
– 100%,
цена после снижения
снижения  – 90%,
– 90%,
 снижения
снижения  – 100%,
– 100%, цена после
 снижения
снижения  – 90%,
– 90%,откуда  (ден. ед.);
(ден. ед.);
 (ден. ед.);
(ден. ед.);4) первоначальная цена  %,
%,
конечная цена %,
%,
 %,
%,конечная цена
 %,
%,откуда  ,
,  %.
%.
 ,
,  %.
%.Ответ: на  %.
%.
 %.
%.Пример 3. Сумма цифр двузначного числа равна  . Если к этому числу прибавить
. Если к этому числу прибавить  , то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
Решение. Пусть исходное число , где
, где  и
и  цифры.
цифры.
Согласно условию задачи составим систему уравнений:

Упростим второе уравнение системы:
 ,
,  ,
,  .
.
Сложим уравнения системы:
Подставляя значение в уравнение
в уравнение  , получим
, получим 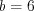 .
.
Запишем искомое число: .
.
Ответ: .
.
 . Если к этому числу прибавить
. Если к этому числу прибавить  , то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число.
, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите исходное число. Решение. Пусть исходное число
 , где
, где  и
и  цифры.
цифры. Согласно условию задачи составим систему уравнений:

Упростим второе уравнение системы:
 ,
,  ,
,  .
. Сложим уравнения системы:

Подставляя значение
 в уравнение
в уравнение  , получим
, получим 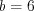 .
. Запишем искомое число:
 .
. Ответ:
 .
.Пример 4. Товарный поезд был задержан в пути на  мин, а затем на расстоянии
мин, а затем на расстоянии  км наверстал упущенное время. Как изменилась при этом его скорость, если первоначально он проходил
км наверстал упущенное время. Как изменилась при этом его скорость, если первоначально он проходил  километров за один час?
километров за один час?
Решение. Полагая, что первоначальная скорость поезда увеличилась на км/ч, составим таблицу:
км/ч, составим таблицу:
 мин, а затем на расстоянии
мин, а затем на расстоянии  км наверстал упущенное время. Как изменилась при этом его скорость, если первоначально он проходил
км наверстал упущенное время. Как изменилась при этом его скорость, если первоначально он проходил  километров за один час?
километров за один час? Решение. Полагая, что первоначальная скорость поезда увеличилась на
 км/ч, составим таблицу:
км/ч, составим таблицу:
Так как время движения поезда сократилось на  мин, что составляет
мин, что составляет  ч, то согласно условию задачи получим уравнение:
ч, то согласно условию задачи получим уравнение:
 км/ч.
км/ч.
 мин, что составляет
мин, что составляет  ч, то согласно условию задачи получим уравнение:
ч, то согласно условию задачи получим уравнение:  км/ч.
км/ч. Ответ: увеличилась на  км/ч.
км/ч.
 км/ч.
км/ч.Пример 5. Моторная лодка прошла расстояние между двумя пунктами по реке туда и обратно, не останавливаясь, за  ч
ч  мин. Расстояние между пунктами
мин. Расстояние между пунктами  км. Определите собственную скорость лодки, если скорость течения реки равна
км. Определите собственную скорость лодки, если скорость течения реки равна  км/ч.
км/ч.
Решение. Пусть собственная скорость лодки равна км/ч.
км/ч.
Составим таблицу:
 ч
ч  мин. Расстояние между пунктами
мин. Расстояние между пунктами  км. Определите собственную скорость лодки, если скорость течения реки равна
км. Определите собственную скорость лодки, если скорость течения реки равна  км/ч.
км/ч. Решение. Пусть собственная скорость лодки равна
 км/ч.
км/ч. Составим таблицу:

Так как  ч
ч  мин
мин  ч
ч ч и
ч и  по теч.+
по теч.+  пр. теч. =
пр. теч. =  ч, то получим уравнение:
ч, то получим уравнение:
 ч
ч  мин
мин  ч
ч ч и
ч и  по теч.+
по теч.+  пр. теч. =
пр. теч. =  ч, то получим уравнение:
ч, то получим уравнение:  ,
,  ,
,  ,
,  , откуда
, откуда  км/ч.
км/ч. Ответ:
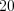 км/ч.
км/ч.Пример 6. Два тела движутся по окружности равномерно в одну сторону. Первое тело проходит окружность на  быстрее второго и догоняет второе тело каждые
быстрее второго и догоняет второе тело каждые  . За сколько секунд второе тело пройдет
. За сколько секунд второе тело пройдет  окружности?
окружности?
Решение. Пусть длина окружности равна .
.
Составим таблицу, учитывая, что первое тело проходит окружность на быстрее второго.
быстрее второго.
 быстрее второго и догоняет второе тело каждые
быстрее второго и догоняет второе тело каждые  . За сколько секунд второе тело пройдет
. За сколько секунд второе тело пройдет  окружности?
окружности? Решение. Пусть длина окружности равна
 .
. Составим таблицу, учитывая, что первое тело проходит окружность на
 быстрее второго.
быстрее второго.
Зная скорость движения каждого тела, составим таблицу, учитывая, что первое тело догоняет второе каждые  :
:
 :
:
Согласно условию задачи второе тело догоняет первое, значит, оно проходит путь  .
.
Получим уравнение .
.
Разделив обе части уравнения на (
(  ), запишем:
), запишем:
 ,
,  ,
,  , откуда
, откуда 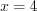 .
.
Найдем время, за которое второе тело проходит всю окружность:
 (с).
(с).
Найдем время, за которое второе тело проходит окружности:
окружности:
 (с).
(с).
Ответ: .
.
 .
. Получим уравнение
 .
. Разделив обе части уравнения на
 (
(  ), запишем:
), запишем:  ,
,  ,
,  , откуда
, откуда 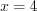 .
. Найдем время, за которое второе тело проходит всю окружность:
 (с).
(с).Найдем время, за которое второе тело проходит
 окружности:
окружности: (с).
(с). Ответ:
 .
.Пример 7. Двое рабочих выполняют совместно некоторое задание за  ч. Первый из них, работая отдельно, может выполнить его на
ч. Первый из них, работая отдельно, может выполнить его на  ч быстрее, чем второй, если тот будет работать отдельно. За сколько часов второй рабочий может выполнить
ч быстрее, чем второй, если тот будет работать отдельно. За сколько часов второй рабочий может выполнить  % задания?
% задания?
Решение. Пусть – объем задания.
– объем задания.
Рассмотрим раздельную работу, учитывая при этом, что каждый рабочий в таком случае выполняет весь объем задания:
 ч. Первый из них, работая отдельно, может выполнить его на
ч. Первый из них, работая отдельно, может выполнить его на  ч быстрее, чем второй, если тот будет работать отдельно. За сколько часов второй рабочий может выполнить
ч быстрее, чем второй, если тот будет работать отдельно. За сколько часов второй рабочий может выполнить  % задания?
% задания? Решение. Пусть
 – объем задания.
– объем задания. Рассмотрим раздельную работу, учитывая при этом, что каждый рабочий в таком случае выполняет весь объем задания:

Зная производительность каждого рабочего, рассмотрим совместную работу:

Согласно условию задачи запишем и решим уравнение:
 ,
,  ,
,  ,
,
 ,
,  , откуда
, откуда  .
.
Если все задание второй рабочий может выполнить за ч, то
ч, то  % задания он выполнит за
% задания он выполнит за
 (ч).
(ч).
Ответ: ч.
ч.
 ,
,  ,
,  ,
,  ,
,  , откуда
, откуда  .
. Если все задание второй рабочий может выполнить за
 ч, то
ч, то  % задания он выполнит за
% задания он выполнит за  (ч).
(ч). Ответ:
 ч.
ч.Пример 8. Через  час после начала равномерного спуска воды в бассейне ее осталось
час после начала равномерного спуска воды в бассейне ее осталось  тонн, а еще через
тонн, а еще через  часа
часа  тонн. Сколько воды было в бассейне?
тонн. Сколько воды было в бассейне?
Решение. Пусть в бассейне было тонн воды.
тонн воды.
Если за час вытекает
час вытекает  тонн воды, то через 1 час после спуска в бассейне останется
тонн воды, то через 1 час после спуска в бассейне останется  или
или  тонн воды.
тонн воды.
Через часа останется
часа останется  тонн воды.
тонн воды.
Вычитая из уравнения уравнение
уравнение  , получим:
, получим:
 (т).
(т).
Ответ: тонн.
тонн.
 час после начала равномерного спуска воды в бассейне ее осталось
час после начала равномерного спуска воды в бассейне ее осталось  тонн, а еще через
тонн, а еще через  часа
часа  тонн. Сколько воды было в бассейне?
тонн. Сколько воды было в бассейне? Решение. Пусть в бассейне было
 тонн воды.
тонн воды. Если за
 час вытекает
час вытекает  тонн воды, то через 1 час после спуска в бассейне останется
тонн воды, то через 1 час после спуска в бассейне останется  или
или  тонн воды.
тонн воды.Через
 часа останется
часа останется  тонн воды.
тонн воды. Вычитая из уравнения
 уравнение
уравнение  , получим:
, получим: (т).
(т). Ответ:
 тонн.
тонн.Пример 9. Смешали 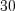 % - й раствор соляной кислоты с
% - й раствор соляной кислоты с  %-м и получили один килограмм
%-м и получили один килограмм  %- го раствора. Сколько граммов каждого раствора было взято?
%- го раствора. Сколько граммов каждого раствора было взято?
Решение. Пусть первого раствора взяли г, а второго
г, а второго  г.
г.
Зная,что в первом растворе содержится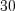 % кислоты, запишем:
% кислоты, запишем:

Зная, что во втором растворе содержится % кислоты, запишем:
% кислоты, запишем:

Если смешать г первого и
г первого и  г второго раствора, то получим третий раствор:
г второго раствора, то получим третий раствор:

Запишем пропорцию:
 %
%
 %
%
Тогда
 , откуда
, откуда  .
.
Так как согласно условию задачи , то, вычитая из уравнения
, то, вычитая из уравнения  уравнение
уравнение  , получим:
, получим:
 .
.
Подставляя значение в уравнение
в уравнение  , найдем значение
, найдем значение  :
:
 .
.
Ответ: г и
г и  г.
г.
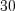 % - й раствор соляной кислоты с
% - й раствор соляной кислоты с  %-м и получили один килограмм
%-м и получили один килограмм  %- го раствора. Сколько граммов каждого раствора было взято?
%- го раствора. Сколько граммов каждого раствора было взято? Решение. Пусть первого раствора взяли
 г, а второго
г, а второго  г.
г. Зная,что в первом растворе содержится
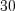 % кислоты, запишем:
% кислоты, запишем: 
Зная, что во втором растворе содержится
 % кислоты, запишем:
% кислоты, запишем: 
Если смешать
 г первого и
г первого и  г второго раствора, то получим третий раствор:
г второго раствора, то получим третий раствор: 
Запишем пропорцию:
 %
%  %
% Тогда

 , откуда
, откуда  .
. Так как согласно условию задачи
 , то, вычитая из уравнения
, то, вычитая из уравнения  уравнение
уравнение  , получим:
, получим: .
. Подставляя значение
 в уравнение
в уравнение  , найдем значение
, найдем значение  :
: .
. Ответ:
 г и
г и  г.
г. 
