Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (5.20)
. (5.20) . (5.24)
. (5.24)  . (5.28)
. (5.28) . (5.29)
. (5.29) или
или  .
.



Тригонометрическими называют уравнения, содержащие тригонометрические функции.
Например, уравнения  и
и  – тригонометрические.
– тригонометрические.
 и
и  – тригонометрические.
– тригонометрические.Простейшие тригонометрические уравнения
1. Если уравнение имеет вид  , то при условии, что
, то при условии, что  ,
,  ,
,
 , то при условии, что
, то при условии, что  ,
,  ,
,  . (5.20)
. (5.20)Частные случаи:
а) если , то
, то 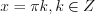 ; (5.21)
; (5.21)
а) если
 , то
, то 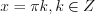 ; (5.21)
; (5.21) б) если  , то
, то 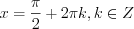 ; (5.22)
; (5.22)
 , то
, то 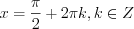 ; (5.22)
; (5.22)в) если  , то
, то 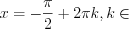
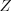 . (5.23)
. (5.23)
 , то
, то 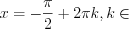
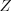 . (5.23)
. (5.23)2. Если уравнение имеет вид  , то при условии, что
, то при условии, что 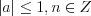 ,
,
 , то при условии, что
, то при условии, что 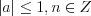 ,
,  . (5.24)
. (5.24)Частные
случаи:
а) если  , то
, то  (5.25)
(5.25)
б) если  , то
, то  ; (5.26)
; (5.26)
 , то
, то  ; (5.26)
; (5.26)в) если  , то
, то 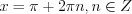 . (5.27)
. (5.27)
 , то
, то 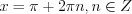 . (5.27)
. (5.27)3. Если уравнение имеет вид  , то при
, то при 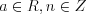 ,
,
 , то при
, то при 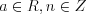 ,
,  . (5.28)
. (5.28)4. Если уравнение имеет вид  , то при
, то при 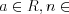
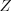
 , то при
, то при 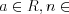
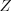
 . (5.29)
. (5.29)Методы решений тригонометрических уравнений
1. Решение однородных
уравнений относительно  x и
x и  .
.
Однородным
уравнением первой степени называют уравнение вида:  . (5.30)
. (5.30)
Чтобы решить однородное уравнение, необходимо разделить обе его части на  :
:
 или
или  ,
,
откуда  ,
,  , где
, где  .
.
 ,
,  , где
, где  .
.Однородным
уравнением второй степени называют уравнение вида:  . (5.31)
. (5.31)
Чтобы решить это уравнение, необходимо разделить обе его части на  :
:
 :
:  или
или  .
. Решая квадратное уравнение относительно  , получим простейшие уравнения вида
, получим простейшие уравнения вида  .
.
 , получим простейшие уравнения вида
, получим простейшие уравнения вида  .
.2. Решение методом введения вспомогательного аргумента уравнений вида:
 . (5.32)
. (5.32)
 . (5.32)
. (5.32)Чтобы ввести вспомогательный аргумент, необходимо
разделить обе части уравнения 5.32 на число
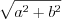 , т. е. записать данное уравнение в виде:
, т. е. записать данное уравнение в виде:
 . (5.32.1)
. (5.32.1)
Применяя подстановку и
и  , получим:
, получим:
 , откуда
, откуда  .
.
Решая это уравнение при условии, что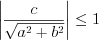 , найдем значения переменной
, найдем значения переменной  :
:
 , где
, где  .
.
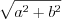 , т. е. записать данное уравнение в виде:
, т. е. записать данное уравнение в виде:  . (5.32.1)
. (5.32.1) Применяя подстановку
 и
и  , получим:
, получим:  , откуда
, откуда  .
. Решая это уравнение при условии, что
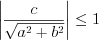 , найдем значения переменной
, найдем значения переменной  :
:  , где
, где  .
.Вспомогательный аргумент  может быть записан в
виде:
может быть записан в
виде:
 или
или  .
.
 может быть записан в
виде:
может быть записан в
виде:  или
или  .
.3. Решение уравнений помощью универсальной тригонометрической подстановки:
 и
и  .
.
В результате подстановки изменится область определения уравнения, что может привести к потере корней.
 и
и  .
. В результате подстановки изменится область определения уравнения, что может привести к потере корней.
С помощью универсальной тригонометрической
подстановки можно решать и уравнение вида:
 .
.
Решая квадратное уравнение относительно , найдем корни уравнения.
, найдем корни уравнения.
 .
. Решая квадратное уравнение относительно
 , найдем корни уравнения.
, найдем корни уравнения.Пример 1. Решите уравнение  .
.
 .
.Решение. Зная, что  , запишем:
, запишем:  .
.
Подставляя значение в исходное уравнение, получим:
в исходное уравнение, получим:
 ,
,
 ,
,
 .
.
Полученное уравнение равносильно совокупности двух простейших уравнений:
1) , откуда по формуле 5.25
, откуда по формуле 5.25
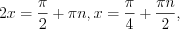 где
где  ;
;
2) , откуда
, откуда  , поскольку областью значений функции
, поскольку областью значений функции  является отрезок
является отрезок ![[-1;1] LaTeX formula: [-1;1]](/uploads/formulas/39c69e02cc294b23aafc11c9f25dc64d7b6685f4.1.1.png) , а число
, а число  не принадлежит этому отрезку.
не принадлежит этому отрезку.
Ответ: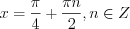 .
.
 , запишем:
, запишем:  .
. Подставляя значение
 в исходное уравнение, получим:
в исходное уравнение, получим:  ,
, ,
, .
. Полученное уравнение равносильно совокупности двух простейших уравнений:
1)
 , откуда по формуле 5.25
, откуда по формуле 5.25 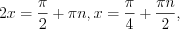 где
где  ;
; 2)
 , откуда
, откуда  , поскольку областью значений функции
, поскольку областью значений функции  является отрезок
является отрезок ![[-1;1] LaTeX formula: [-1;1]](/uploads/formulas/39c69e02cc294b23aafc11c9f25dc64d7b6685f4.1.1.png) , а число
, а число  не принадлежит этому отрезку.
не принадлежит этому отрезку. Ответ:
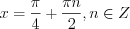 .
.Пример 2. Найдите сумму всех корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку ![[-\pi;0] LaTeX formula: [-\pi;0]](/uploads/formulas/842a820c9f3445985531b2f22da71d83895c78c5.1.1.png) .
.
 , принадлежащих отрезку
, принадлежащих отрезку ![[-\pi;0] LaTeX formula: [-\pi;0]](/uploads/formulas/842a820c9f3445985531b2f22da71d83895c78c5.1.1.png) .
.Решение. Учитывая основной период функции синус и применяя формулу приведения, получим:
 ,
,
 ,
,  .
.
 ,
, ,
,  .
. 2)  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
, Произведем отбор корней уравнения на отрезке ![[-\pi;0] LaTeX formula: [-\pi;0]](http://helpy.quali.me/uploads/formulas/842a820c9f3445985531b2f22da71d83895c78c5.1.1.png) (рис. 5.9).
(рис. 5.9).
![[-\pi;0] LaTeX formula: [-\pi;0]](http://helpy.quali.me/uploads/formulas/842a820c9f3445985531b2f22da71d83895c78c5.1.1.png) (рис. 5.9).
(рис. 5.9). 
Если  то при
то при 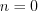 получим
получим  , а при
, а при 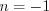 получим
получим 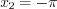 .
.
 то при
то при 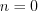 получим
получим  , а при
, а при 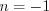 получим
получим 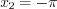 .
.Если 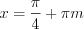 , то при
, то при 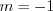 получим
получим 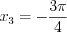 .
.
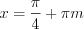 , то при
, то при 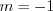 получим
получим 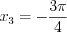 .
. Найдем сумму полученных корней уравнения: 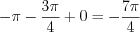 .
.
Ответ: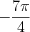 .
.
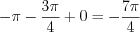 .
. Ответ:
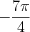 .
.Пример 3. Укажите количество корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку ![[0;\pi] LaTeX formula: [0;\pi]](/uploads/formulas/afb897bb69d12c200693ec6f07caedbe8c1d4f84.1.1.png) .
.
 , принадлежащих отрезку
, принадлежащих отрезку ![[0;\pi] LaTeX formula: [0;\pi]](/uploads/formulas/afb897bb69d12c200693ec6f07caedbe8c1d4f84.1.1.png) .
.Решение. Так как  , то
, то
 ,
,
 .
.
Получили уравнение вида 5.31.
Разделим обе его части на и решим квадратное уравнение относительно
и решим квадратное уравнение относительно  :
:
 , откуда
, откуда  и
и  .
.
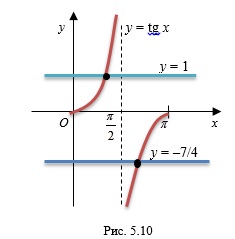
На отрезке![[0;\pi] LaTeX formula: [0;\pi]](http://helpy.quali.me/uploads/formulas/afb897bb69d12c200693ec6f07caedbe8c1d4f84.1.1.png) построим графики функций
построим графики функций  ,
,  и
и  (рис. 5.10).
(рис. 5.10).
 , то
, то ,
, .
. Получили уравнение вида 5.31.
Разделим обе его части на
 и решим квадратное уравнение относительно
и решим квадратное уравнение относительно  :
:  , откуда
, откуда  и
и  .
. На отрезке
![[0;\pi] LaTeX formula: [0;\pi]](http://helpy.quali.me/uploads/formulas/afb897bb69d12c200693ec6f07caedbe8c1d4f84.1.1.png) построим графики функций
построим графики функций  ,
,  и
и  (рис. 5.10).
(рис. 5.10).
Так как график функции  пересекает прямые
пересекает прямые  и
и  в двух точках, то исходное уравнение имеет два корня.
в двух точках, то исходное уравнение имеет два корня.
Ответ: .
.
 пересекает прямые
пересекает прямые  и
и  в двух точках, то исходное уравнение имеет два корня.
в двух точках, то исходное уравнение имеет два корня. Ответ:
 .
.Пример 4. Решите уравнение  .
.
 .
.Решение. Имеем уравнение 5.31, которое приведем к виду 5.32.1.
Разделив обе части уравнения на число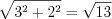 , получим:
, получим:
 .
.
Разделив обе части уравнения на число
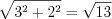 , получим:
, получим: .
. Применим подстановку  откуда
откуда  .
.
Уравнение примет вид:
 или
или  .
.
По формуле 5.20, получим:
 , где
, где  ,
,
 , где
, где  ,
,
 , где
, где  .
.
 откуда
откуда  .
. Уравнение примет вид:
 или
или  .
. По формуле 5.20, получим:
 , где
, где  ,
, , где
, где  ,
, , где
, где  .
.Ответ:  ,
,  .
.
 ,
,  .
.Пример 5. Найдите среднее арифметическое корней уравнения  .
.
 .
.Решение. Зная, что областью определения функции арккосинус является отрезок ![[-1;1] LaTeX formula: [-1;1]](/uploads/formulas/39c69e02cc294b23aafc11c9f25dc64d7b6685f4.1.1.png) , запишем ОДЗ уравнения:
, запишем ОДЗ уравнения:
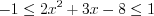 .
.
Заменим данное уравнение равносильным ему на ОДЗ уравнением:
 или
или  , откуда
, откуда 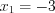 и
и  .
.
Так как оба полученных корня принадлежат области допустимых значений уравнения, то найдем их среднее арифметическое:
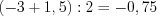 .
.
Ответ: .
.
![[-1;1] LaTeX formula: [-1;1]](/uploads/formulas/39c69e02cc294b23aafc11c9f25dc64d7b6685f4.1.1.png) , запишем ОДЗ уравнения:
, запишем ОДЗ уравнения: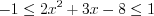 .
. Заменим данное уравнение равносильным ему на ОДЗ уравнением:
 или
или  , откуда
, откуда 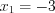 и
и  .
. Так как оба полученных корня принадлежат области допустимых значений уравнения, то найдем их среднее арифметическое:
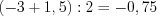 .
. Ответ:
 .
.Пример 6. Найдите число решений уравнения  , если
, если ![x,y \in \left [-\frac{\pi }{2};\pi \right ] LaTeX formula: x,y \in \left [-\frac{\pi }{2};\pi \right ]](/uploads/formulas/7f78099f37f75b17c58e2f61f06cd71de0bb1918.1.1.png) .
.
 , если
, если ![x,y \in \left [-\frac{\pi }{2};\pi \right ] LaTeX formula: x,y \in \left [-\frac{\pi }{2};\pi \right ]](/uploads/formulas/7f78099f37f75b17c58e2f61f06cd71de0bb1918.1.1.png) .
.Решение.Так как  и
и  , то данное уравнение равносильно системе уравнений:
, то данное уравнение равносильно системе уравнений:
 и
и  , то данное уравнение равносильно системе уравнений:
, то данное уравнение равносильно системе уравнений: 
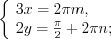

Проведем отбор корней уравнения на отрезке ![\left [ -\frac{\pi }{2};\pi \right ] LaTeX formula: \left [ -\frac{\pi }{2};\pi \right ]](/uploads/formulas/4773ea029c278f879acd83f5784d72bf50dc7eb5.1.1.png) :
:
если , то
, то  ; если
; если 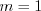 , то
, то 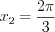 ; если
; если 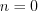 , то
, то 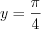 .
.
Получили две пары решений уравнения: и
и  .
.
Ответ: .
.
![\left [ -\frac{\pi }{2};\pi \right ] LaTeX formula: \left [ -\frac{\pi }{2};\pi \right ]](/uploads/formulas/4773ea029c278f879acd83f5784d72bf50dc7eb5.1.1.png) :
: если
 , то
, то  ; если
; если 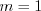 , то
, то 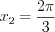 ; если
; если 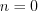 , то
, то 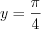 .
. Получили две пары решений уравнения:
 и
и  .
. Ответ:
 .
.1. Уравнения  и
и  имеют решения только при
имеют решения только при  .
.
 и
и  имеют решения только при
имеют решения только при  .
.2. Уравнения  и
и  имеют решения при
имеют решения при  .
.
 и
и  имеют решения при
имеют решения при  .
.