Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты


Множество целых чисел состоит из натуральных чисел, противоположных им чисел и числа нуль.
Множество всех целых чисел обозначают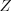 .
.
Это множество чисел бесконечно: …,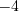 ,
, 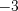 ,
, 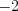 ,
,  ,
,  ,
,  ,
,  , … .
, … .
Множество всех целых чисел обозначают
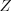 .
. Это множество чисел бесконечно: …,
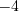 ,
, 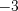 ,
, 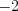 ,
,  ,
,  ,
,  ,
,  , … .
, … . Числовая ось или числовая прямая – это прямая, на которой определено начало отсчета, направление отсчета и единичный отрезок.
На рисунке 1.1 точка – начало отсчета, отрезок
– начало отсчета, отрезок 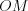 имеет длину, равную единице, а стрелка указывает положительное направление отсчета. Начало отсчета (точка
имеет длину, равную единице, а стрелка указывает положительное направление отсчета. Начало отсчета (точка  ) и число нуль совпадают.
) и число нуль совпадают.
Числа, расположенные на числовой оси справа от начала отсчета, называют положительными числами, а числа, расположенные слева от начала отсчета, называют отрицательными.
На рисунке 1.1 точка
 – начало отсчета, отрезок
– начало отсчета, отрезок 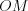 имеет длину, равную единице, а стрелка указывает положительное направление отсчета. Начало отсчета (точка
имеет длину, равную единице, а стрелка указывает положительное направление отсчета. Начало отсчета (точка  ) и число нуль совпадают.
) и число нуль совпадают. Числа, расположенные на числовой оси справа от начала отсчета, называют положительными числами, а числа, расположенные слева от начала отсчета, называют отрицательными.

Перед отрицательными числами всегда ставят знак «  ». Натуральные числа – положительные. Перед положительными числами можно поставить знак «
». Натуральные числа – положительные. Перед положительными числами можно поставить знак «  ».
».
 ». Натуральные числа – положительные. Перед положительными числами можно поставить знак «
». Натуральные числа – положительные. Перед положительными числами можно поставить знак «  ».
». Числа  и
и  называют противоположными.
называют противоположными.
Сумма двух противоположных чисел всегда равна нулю.
Н а п р и м е р, ;
;  .
.
 и
и  называют противоположными.
называют противоположными. Сумма двух противоположных чисел всегда равна нулю.
Н а п р и м е р,
 ;
;  .
.Сравнение целых чисел с помощью числовой прямой
Из двух чисел больше то число, которое расположено правее на числовой прямой, и меньше то число, которое расположено левее на этой прямой.
Н а п р и м е р, на рисунке 1.2 число расположено правее числа
расположено правее числа 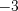 , значит число
, значит число  больше числа
больше числа 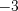 , а число
, а число 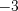 в свою очередь меньше числа
в свою очередь меньше числа  .
.
Н а п р и м е р, на рисунке 1.2 число
 расположено правее числа
расположено правее числа 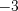 , значит число
, значит число  больше числа
больше числа 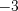 , а число
, а число 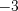 в свою очередь меньше числа
в свою очередь меньше числа  .
.Числовые неравенства
Два числа  и
и  , соединенные одним из знаков
, соединенные одним из знаков  (больше),
(больше),  (меньше),
(меньше),  (больше или равно) или
(больше или равно) или  (меньше или равно), называют числовым неравенством:
(меньше или равно), называют числовым неравенством:
 ,
, 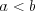 ,
, 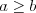 ,
,  .
.
 и
и  , соединенные одним из знаков
, соединенные одним из знаков  (больше),
(больше),  (меньше),
(меньше),  (больше или равно) или
(больше или равно) или  (меньше или равно), называют числовым неравенством:
(меньше или равно), называют числовым неравенством:  ,
, 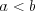 ,
, 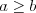 ,
,  .
. Если число  неотрицательное, то пишут
неотрицательное, то пишут  и читают:
и читают:  больше или равно нулю.
больше или равно нулю.
Если число неположительное, то есть отрицательное или число
неположительное, то есть отрицательное или число  , то пишут
, то пишут  и читают:
и читают:  меньше или равно нулю.
меньше или равно нулю.
Если число положительное, то записывают
положительное, то записывают  , а если число
, а если число  отрицательное, то записывают
отрицательное, то записывают  .
.
Неравенство, содержащее знак или знак
или знак  называют строгим неравенством, а содержащее знак
называют строгим неравенством, а содержащее знак  или знак
или знак  – нестрогим неравенством.
– нестрогим неравенством.
Если оба неравенства содержат один и тот же знак (знак или знак
или знак  ), то их называют неравенствами одинакового смысла. Если же одно из неравенств содержит знак
), то их называют неравенствами одинакового смысла. Если же одно из неравенств содержит знак  , а другое знак
, а другое знак  , то такие неравенства называют неравенствами противоположного смысла.
, то такие неравенства называют неравенствами противоположного смысла.
 неотрицательное, то пишут
неотрицательное, то пишут  и читают:
и читают:  больше или равно нулю.
больше или равно нулю. Если число
 неположительное, то есть отрицательное или число
неположительное, то есть отрицательное или число  , то пишут
, то пишут  и читают:
и читают:  меньше или равно нулю.
меньше или равно нулю. Если число
 положительное, то записывают
положительное, то записывают  , а если число
, а если число  отрицательное, то записывают
отрицательное, то записывают  .
.Неравенство, содержащее знак
 или знак
или знак  называют строгим неравенством, а содержащее знак
называют строгим неравенством, а содержащее знак  или знак
или знак  – нестрогим неравенством.
– нестрогим неравенством. Если оба неравенства содержат один и тот же знак (знак
 или знак
или знак  ), то их называют неравенствами одинакового смысла. Если же одно из неравенств содержит знак
), то их называют неравенствами одинакового смысла. Если же одно из неравенств содержит знак  , а другое знак
, а другое знак  , то такие неравенства называют неравенствами противоположного смысла.
, то такие неравенства называют неравенствами противоположного смысла.Неравенства  ,
,  ,
,  и
и  называют двойными неравенствами.
называют двойными неравенствами.
Неравенство читают так: число
читают так: число  больше числа
больше числа  , но меньше числа
, но меньше числа  .
.
Неравенство читают так: число
читают так: число  больше или равно числу
больше или равно числу  , но меньше или равно числу
, но меньше или равно числу  или число
или число  не меньше числа
не меньше числа  и не больше числа
и не больше числа  .
.
Двойные неравенства можно заменять системами неравенств.
Н а п р и м е р, неравенство заменяют системой неравенств
заменяют системой неравенств 
 ,
,  ,
,  и
и  называют двойными неравенствами.
называют двойными неравенствами. Неравенство
 читают так: число
читают так: число  больше числа
больше числа  , но меньше числа
, но меньше числа  .
. Неравенство
 читают так: число
читают так: число  больше или равно числу
больше или равно числу  , но меньше или равно числу
, но меньше или равно числу  или число
или число  не меньше числа
не меньше числа  и не больше числа
и не больше числа  .
. Двойные неравенства можно заменять системами неравенств.
Н а п р и м е р, неравенство
 заменяют системой неравенств
заменяют системой неравенств 
Свойства числовых неравенств
1. Если  и
и  , то
, то  , или если
, или если 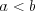 и
и  , то
, то  .
.
 и
и  , то
, то  , или если
, или если 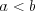 и
и  , то
, то  .
. 2. Если  и
и  , то
, то  , или если
, или если 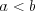 и
и  , то
, то  .
.
 и
и  , то
, то  , или если
, или если 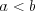 и
и  , то
, то  .
. 3. Если  и
и  , то
, то  , или если
, или если 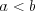 и
и  , то
, то  .
.
 и
и  , то
, то  , или если
, или если 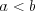 и
и  , то
, то  .
. 4. Если  , то
, то  , или если
, или если 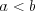 , то
, то  при условии, что
при условии, что  .
.
 , то
, то  , или если
, или если 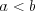 , то
, то  при условии, что
при условии, что  .
. 5. Если  и
и  , то
, то  , или если
, или если 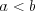 и
и  , то
, то  .
.
 и
и  , то
, то  , или если
, или если 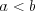 и
и  , то
, то  .
. 6. Если 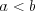 и
и  – натуральное число, то
– натуральное число, то  .
.
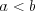 и
и  – натуральное число, то
– натуральное число, то  .
. 7. Если 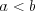 и
и  – натуральное число, то
– натуральное число, то  при условии, что
при условии, что  и
и 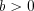 .
.
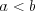 и
и  – натуральное число, то
– натуральное число, то  при условии, что
при условии, что  и
и 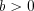 .
. 8. Если  , то
, то  . Если
. Если  , то
, то  .
.
 , то
, то  . Если
. Если  , то
, то  .
. Абсолютная величина числа
Модулем (абсолютной величиной) числа  называют число
называют число  , если оно неотрицательное, и противоположное ему число, если
, если оно неотрицательное, и противоположное ему число, если  отрицательное:
отрицательное:
 , если
, если  и
и  , если
, если  .
.
Н а п р и м е р: ;
;  ;
;  .
.
 называют число
называют число  , если оно неотрицательное, и противоположное ему число, если
, если оно неотрицательное, и противоположное ему число, если  отрицательное:
отрицательное:  , если
, если  и
и  , если
, если  .
. Н а п р и м е р:
 ;
;  ;
;  .
.Геометрический смысл модуля числа: модуль числа – это расстояние от начала отсчета до точки на числовой прямой, соответствующей этому числу (рис. 1.3).

Свойства модуля числа:
1) ;
;
2) ;
;
3) ;
;
4) ;
;
5) ;
;
6) .
.
1)
 ;
; 2)
 ;
; 3)
 ;
; 4)
 ;
; 5)
 ;
;6)
 .
. Решение простейших уравнений, содержащих переменную под знаком модуля
Поскольку модуль любого числа – величина неотрицательная, то уравнение  имеет решения, если
имеет решения, если  и не имеет решений, если
и не имеет решений, если  .
.
Н а п р и м е р:
1) решение уравнения образуют числа
образуют числа  и
и 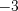 ;
;
2) решением уравнения является число
является число  ;
;
3) уравнение решений не имеет.
решений не имеет.
 имеет решения, если
имеет решения, если  и не имеет решений, если
и не имеет решений, если  .
. Н а п р и м е р:
1) решение уравнения
 образуют числа
образуют числа  и
и 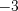 ;
;2) решением уравнения
 является число
является число  ;
;3) уравнение
 решений не имеет.
решений не имеет.Решение простейших неравенств, содержащих переменную под знаком модуля
Решение неравенства  записывают так:
записывают так:  .
.
 записывают так:
записывают так:  .
.Решение неравенства  записывают так:
записывают так:  .
.
 записывают так:
записывают так:  .
.Решение неравенства  записывают так:
записывают так:  или
или  .
.
 записывают так:
записывают так:  или
или  .
.Решение неравенства  записывают так:
записывают так:  или
или  .
.
 записывают так:
записывают так:  или
или  .
.Правила сравнения целых чисел
1. Из двух положительных чисел больше то число, модуль которого больше.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
.2. Из двух отрицательных чисел больше то число, модуль которого меньше.
Н а п р и м е р, , так как
, так как  .
.
Н а п р и м е р,
 , так как
, так как  .
.3. Любое положительное число больше любого отрицательного числа и числа нуль.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
. 4. Любое отрицательное число меньше любого положительного числа и числа нуль.
Н а п р и м е р, .
.
Н а п р и м е р,
 .
.Правила сложения целых чисел
1. Чтобы сложить два числа с одинаковыми знаками, необходимо сложить их модули и перед результатом поставить общий знак этих чисел.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
.2. Чтобы сложить два числа с противоположными знаками, необходимо из большего модуля числа вычесть меньший и перед результатом поставить знак числа, модуль которого больше.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
.3. Чтобы из одного числа вычесть другое, можно к уменьшаемому прибавить число, противоположное вычитаемому.
Н а п р и м е р: .
.
Н а п р и м е р:
 .
. Правила умножения и деления целых чисел
1. Чтобы умножить (разделить) два числа с одинаковыми знаками, необходимо модули этих чисел умножить (разделить). В результате всегда будем получать положительное число.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
.2. Чтобы умножить (разделить) два числа с противоположными знаками, необходимо модули этих чисел перемножить (разделить) и перед результатом поставить знак минус. В результате всегда будем получать отрицательное число.
Н а п р и м е р: ;
;  .
.
Н а п р и м е р:
 ;
;  .
.3. При умножении любого числа на число  всегда будем получать число
всегда будем получать число  . При делении числа
. При делении числа  на положительное или отрицательное число всегда будем получать число
на положительное или отрицательное число всегда будем получать число  .
.
Н а п р и м е р: ;
;  .
.
 всегда будем получать число
всегда будем получать число  . При делении числа
. При делении числа  на положительное или отрицательное число всегда будем получать число
на положительное или отрицательное число всегда будем получать число  .
. Н а п р и м е р:
 ;
;  .
.Пример 1. Решите неравенства:  ,
,  ,
,  ,
,  .
.
Решение:
1) если , то
, то  ;
;
2) если , то
, то  или
или  ;
;
3) неравенство решений не имеет, поскольку левая часть этого неравенства всегда неотрицательна, а правая его часть отрицательна, а положительные числа и число
решений не имеет, поскольку левая часть этого неравенства всегда неотрицательна, а правая его часть отрицательна, а положительные числа и число  не могут быть меньше отрицательного числа или быть ему равны;
не могут быть меньше отрицательного числа или быть ему равны;
4) решением неравенства является любое число, поскольку левая часть этого неравенства всегда неотрицательна, а его правая часть отрицательна, а любое положительное число и число
является любое число, поскольку левая часть этого неравенства всегда неотрицательна, а его правая часть отрицательна, а любое положительное число и число  всегда больше отрицательного.
всегда больше отрицательного.
 ,
,  ,
,  ,
,  .
. Решение:
1) если
 , то
, то  ;
; 2) если
 , то
, то  или
или  ;
; 3) неравенство
 решений не имеет, поскольку левая часть этого неравенства всегда неотрицательна, а правая его часть отрицательна, а положительные числа и число
решений не имеет, поскольку левая часть этого неравенства всегда неотрицательна, а правая его часть отрицательна, а положительные числа и число  не могут быть меньше отрицательного числа или быть ему равны;
не могут быть меньше отрицательного числа или быть ему равны; 4) решением неравенства
 является любое число, поскольку левая часть этого неравенства всегда неотрицательна, а его правая часть отрицательна, а любое положительное число и число
является любое число, поскольку левая часть этого неравенства всегда неотрицательна, а его правая часть отрицательна, а любое положительное число и число  всегда больше отрицательного.
всегда больше отрицательного.Пример 2. Вычислите  .
.
Решение. Выполним действия:
1) ;
;
2) ;
;
3) ;
;
4) ;
;
5) .
.
Ответ: .
.
 .
. Решение. Выполним действия:
1)
 ;
; 2)
 ;
; 3)
 ;
; 4)
 ;
;5)
 .
.Ответ:
 .
.1. Число  не является ни положительным, ни отрицательным. Все положительные числа и число
не является ни положительным, ни отрицательным. Все положительные числа и число  называют неотрицательными, а все отрицательные числа и число
называют неотрицательными, а все отрицательные числа и число  называют неположительными.
называют неположительными.
 не является ни положительным, ни отрицательным. Все положительные числа и число
не является ни положительным, ни отрицательным. Все положительные числа и число  называют неотрицательными, а все отрицательные числа и число
называют неотрицательными, а все отрицательные числа и число  называют неположительными.
называют неположительными. 2. Поскольку вычитание всегда можно заменить сложением, то выражения, соединенные знаками «  » и «
» и «  », называют алгебраической суммой.
», называют алгебраической суммой.
 » и «
» и «  », называют алгебраической суммой.
», называют алгебраической суммой.3. Деление любого числа на число  не имеет смысла.
не имеет смысла.
 не имеет смысла.
не имеет смысла.4. Неравенство  не имеет решений, а решением неравенства
не имеет решений, а решением неравенства  является только число
является только число  ; неравенство
; неравенство  также не имеет решений, если
также не имеет решений, если  отрицательное число;
отрицательное число;
 не имеет решений, а решением неравенства
не имеет решений, а решением неравенства  является только число
является только число  ; неравенство
; неравенство  также не имеет решений, если
также не имеет решений, если  отрицательное число;
отрицательное число; 5. Решением неравенства  , при условии, что
, при условии, что  отрицательное число или число
отрицательное число или число  , является любое число, а решением неравенства
, является любое число, а решением неравенства  является любое число, за исключением числа
является любое число, за исключением числа  .
.
 , при условии, что
, при условии, что  отрицательное число или число
отрицательное число или число  , является любое число, а решением неравенства
, является любое число, а решением неравенства  является любое число, за исключением числа
является любое число, за исключением числа  .
. 
