Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 ; (3.15)
; (3.15)  ; (3.21)
; (3.21)  ; (3.16)
; (3.16)  ; (3.22)
; (3.22)  ; (3.17)
; (3.17)  ; (3.23)
; (3.23) ; (3.18)
; (3.18)  ; (3.24)
; (3.24)  ; (3.19)
; (3.19)  ; (3.25)
; (3.25) ; (3.20)
; (3.20)  . (3.26)
. (3.26) . (3.27)
. (3.27)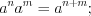
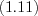
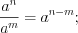
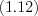
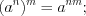

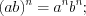
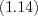
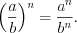
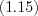
 ,
,
 ,
, ,
,  .
.
Логарифмическими называют уравнения, содержащие переменную под знаком логарифма.
Н а п р и м е р, это может быть уравнение вида:  , где
, где 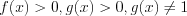 .
.
 , где
, где 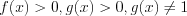 .
.Методы решений уравнений
1. Если уравнение имеет
вид  , (5.18)
, (5.18)
 , (5.18)
, (5.18) то оно равносильно уравнению  (5.18.1)
(5.18.1)
при условии, что и
и 

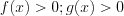 .
.
 (5.18.1)
(5.18.1) при условии, что
 и
и 

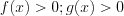 .
. 2. Если уравнение имеет
вид  , (5.19)
, (5.19)
 , (5.19)
, (5.19) то оно равносильно уравнению 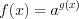 (5.19.1)
(5.19.1)
при условии, что и
и  .
.
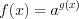 (5.19.1)
(5.19.1) при условии, что
 и
и  .
. 3. Метод подстановки.
4. Использование монотонности функций.
Свойства логарифмов:
 ; (3.15)
; (3.15)  ; (3.21)
; (3.21) ; (3.16)
; (3.16)  ; (3.22)
; (3.22)  ; (3.17)
; (3.17)  ; (3.23)
; (3.23) ; (3.18)
; (3.18)  ; (3.24)
; (3.24)  ; (3.19)
; (3.19)  ; (3.25)
; (3.25) ; (3.20)
; (3.20)  . (3.26)
. (3.26)Свойства 3.15 – 3.26 справедливы при  и
и 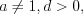 и
и 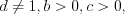 причем числа
причем числа 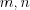 и
и  отличны от нуля.
отличны от нуля.
 и
и 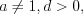 и
и 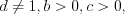 причем числа
причем числа 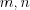 и
и  отличны от нуля.
отличны от нуля. Основное логарифмическое тождество:
 . (3.27)
. (3.27)Свойства степеней:
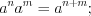
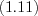
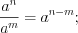
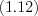
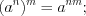

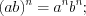
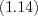
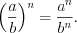
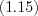
Пример 1. Решите уравнение  .
.
 .
. Решение. ОДЗ: 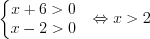 .
.
Согласно свойству 3.18 получим: .
.
Имеем уравнение вида 5.18, которое равносильно уравнению 5.18.1:
 ,
,  .
.
Решим иррациональное уравнение:
 ,
,  ,
,
 ,
,  ,
,
откуда ,
,  – посторонний корень уравнения.
– посторонний корень уравнения.
Ответ: .
.
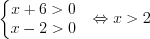 .
. Согласно свойству 3.18 получим:
 .
. Имеем уравнение вида 5.18, которое равносильно уравнению 5.18.1:
 ,
,  .
. Решим иррациональное уравнение:
 ,
,  ,
,  ,
,  ,
, откуда
 ,
,  – посторонний корень уравнения.
– посторонний корень уравнения. Ответ:
 .
.Пример 2. Решите уравнение  .
.
 .
.Решение. ОДЗ: 

По формулам 3.21 и 3.27 выполним преобразования правой части уравнения:
 .
.
Так как имеем уравнение вида 5.19 , то исходное уравнение на ОДЗ равносильно уравнению 5.19.1:
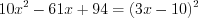 ,
,
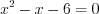 , откуда
, откуда 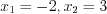 .
.
Так как числа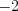 и
и  не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
Ответ: .
.
 .
. Так как имеем уравнение вида 5.19 , то исходное уравнение на ОДЗ равносильно уравнению 5.19.1:
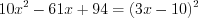 ,
, 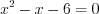 , откуда
, откуда 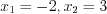 .
. Так как числа
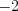 и
и  не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
не принадлежат области допустимых значений уравнения, то уравнение корней не имеет. Ответ:
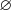 .
.Пример 3. Решите уравнение  .
.
 .
.Решение. ОДЗ: 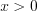 .
.
Полагая , запишем
, запишем 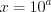 .
.
Решим показательное уравнение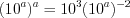 .
.
Применяя свойства степеней 1.13 и 1.11, получим:
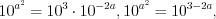
откуда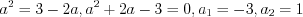 .
.
Учитывая подстановку, найдем корни исходного уравнения:
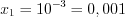 и
и 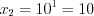 .
.
Ответ: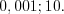
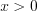 .
. Полагая
 , запишем
, запишем 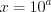 .
. Решим показательное уравнение
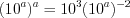 .
. Применяя свойства степеней 1.13 и 1.11, получим:
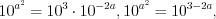
откуда
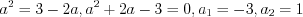 .
. Учитывая подстановку, найдем корни исходного уравнения:
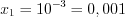 и
и 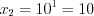 .
. Ответ:
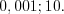
Пример 4. Решите уравнение  .
.
 .
.Решение. ОДЗ: 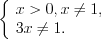
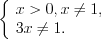
 ,
,  ,
, ,
,  .
.В результате подстановки  получим:
получим:
 ,
,  ,
, 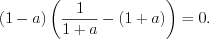
 получим:
получим:  ,
,  ,
, 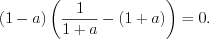
Решим два уравнения:
1)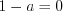 , откуда
, откуда 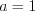 ;
;
2)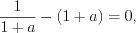
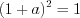 , откуда
, откуда  и
и 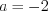 .
.
1)
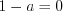 , откуда
, откуда 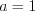 ;
; 2)
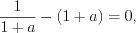
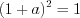 , откуда
, откуда  и
и 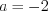 .
. Учитывая подстановку, решим уравнения:
1) , откуда
, откуда  ;
;
2) , откуда
, откуда  – посторонний корень;
– посторонний корень;
3) , откуда
, откуда 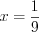 .
.
Ответ: ,
,  .
.
1)
 , откуда
, откуда  ;
; 2)
 , откуда
, откуда  – посторонний корень;
– посторонний корень; 3)
 , откуда
, откуда 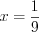 .
. Ответ:
 ,
,  .
.Пример 5. Решите систему уравнений 

Решение. ОДЗ: 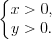
Запишем систему уравнений в виде:
Рассматриваемая система равносильна системе уравнений:

Выразим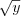 из первого уравнения системы:
из первого уравнения системы: 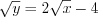 .
.
Подставим полученное выражение во второе уравнение системы:
 ,
,  ,
,  .
.
Получили квадратное уравнение относительно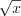 .
.
Значит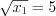 , откуда
, откуда 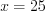 и
и 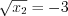 , откуда
, откуда  .
.
Найдем значения переменной :
:
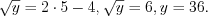
Ответ: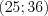 .
.
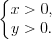
Запишем систему уравнений в виде:

Рассматриваемая система равносильна системе уравнений:

Выразим
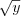 из первого уравнения системы:
из первого уравнения системы: 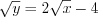 .
. Подставим полученное выражение во второе уравнение системы:
 ,
,  ,
,  .
. Получили квадратное уравнение относительно
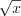 .
. Значит
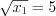 , откуда
, откуда 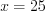 и
и 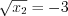 , откуда
, откуда  .
. Найдем значения переменной
 :
: 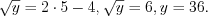
Ответ:
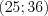 .
.1. Аргумент логарифмической функции всегда положительный, а ее основание положительное и к тому же не равно числу  .
.
 .
.2. Значение логарифма может быть положительным числом, отрицательным числом и числом  .
.
 .
.

 ,
,