Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
 . (5.16.1)
. (5.16.1)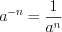 ; (1.9)
; (1.9) . (1.10)
. (1.10) 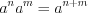 ; (1.11)
; (1.11) 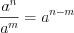 ; (1.12)
; (1.12) 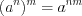 ; (1.13)
; (1.13) 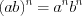 ; (1.14)
; (1.14) . (1.15)
. (1.15)
Пример 1. Найдите сумму корней уравнения
Имеем уравнение вида 5.16, которое равносильно уравнению 5.16.1:
Найдем сумму корней уравнения:
Ответ:

 .
.
Показательными называют уравнения, содержащие переменную в показателе степени, то есть
уравнения вида  , где
, где 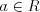 и
и  , причем,
, причем,  и
и 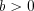 ,
,  .
.
 , где
, где 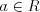 и
и  , причем,
, причем,  и
и 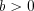 ,
,  .
. Если 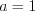 , то уравнение
, то уравнение  примет вид
примет вид  , а его решением является любое из чисел, принадлежащих области определения данного уравнения.
, а его решением является любое из чисел, принадлежащих области определения данного уравнения.
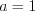 , то уравнение
, то уравнение  примет вид
примет вид  , а его решением является любое из чисел, принадлежащих области определения данного уравнения.
, а его решением является любое из чисел, принадлежащих области определения данного уравнения. Например:
1) решение уравнения образуют все числа, удовлетворяющие условию
образуют все числа, удовлетворяющие условию  ;
;
2) решением уравнения является любое действительное число.
является любое действительное число.
1) решение уравнения
 образуют все числа, удовлетворяющие условию
образуют все числа, удовлетворяющие условию  ;
; 2) решением уравнения
 является любое действительное число.
является любое действительное число.Методы решений уравнений
1. Если уравнение имеет
вид  , (5.16)
, (5.16)
 , (5.16)
, (5.16)то при  и
и  , оно равносильно уравнению
, оно равносильно уравнению
 и
и  , оно равносильно уравнению
, оно равносильно уравнению . (5.16.1)
. (5.16.1)2. Если уравнение имеет
вид  , (5.17)
, (5.17)
 , (5.17)
, (5.17)то оно равносильно уравнению  . (5.17.1)
. (5.17.1)
 . (5.17.1)
. (5.17.1)Степень с целым отрицательным показателем
Для любых действительных чисел  и
и  , при условии, что
, при условии, что  и
и 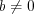 , справедливы равенства:
, справедливы равенства:
 и
и  , при условии, что
, при условии, что  и
и 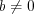 , справедливы равенства:
, справедливы равенства: 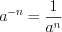 ; (1.9)
; (1.9) . (1.10)
. (1.10)Свойства степеней:
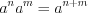 ; (1.11)
; (1.11) 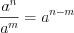 ; (1.12)
; (1.12)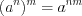 ; (1.13)
; (1.13) 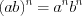 ; (1.14)
; (1.14) . (1.15)
. (1.15)Пример 1. Найдите сумму корней уравнения 
Решение. Применяя свойства степеней 1.13 , 1.11 и 1.14 получим:
Имеем уравнение вида 5.16, которое равносильно уравнению 5.16.1:
 ,
,  ,
,  , откуда
, откуда  .
.
Найдем сумму корней уравнения:  .
.
Ответ:  .
.
Пример 2. Решите уравнение 

Решение. Запишем уравнение в виде:
 .
.
В левой и правой части уравнения вынесем степени с показателем :
:
 ,
,
 ,
,
 .
.
Разделим обе части уравнения на и на
и на  :
:

 .
. В левой и правой части уравнения вынесем степени с показателем
 :
:  ,
,  ,
,  .
. Разделим обе части уравнения на
 и на
и на  :
: 
Пример 3. Найдите модуль разности корней уравнения  .
.
 .
.
 .
. В результате подстановки  уравнение примет вид:
уравнение примет вид:
 откуда
откуда 
Учитывая подстановку , решим два уравнения:
, решим два уравнения:
1) откуда
откуда 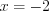 ;
;
 уравнение примет вид:
уравнение примет вид: откуда
откуда 
Учитывая подстановку
 , решим два уравнения:
, решим два уравнения: 1)
 откуда
откуда 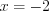 ;
; 2)  откуда
откуда  .
.
Найдем модуль разности корней уравнения: .
.
Ответ: .
.
 откуда
откуда  .
. Найдем модуль разности корней уравнения:
 .
. Ответ:
 .
.Пример 4. Решите уравнение  .
.
 .
.Решение. Пусть  , тогда
, тогда  .
.
 , тогда
, тогда  .
.Действительно, в результате умножения левых и правых частей этих равенств получим:

 ,
,
 ,
,  ,
,  .
.
Рассмотрим уравнение или
или  , откуда
, откуда
 ,
,  .
.

 ,
,  ,
,  ,
,  .
. Рассмотрим уравнение
 или
или  , откуда
, откуда ,
,  .
. Учитывая подстановку  , решим уравнения:
, решим уравнения:
1)

 откуда
откуда  ;
;
2) откуда
откуда 
 .
.
Ответ: .
.
 , решим уравнения:
, решим уравнения: 1)


 откуда
откуда  ;
; 2)
 откуда
откуда 
 .
. Ответ:
 .
.Пример 5. Найдите число корней уравнения  .
.
 .
.Решение. Поскольку  , то имеем уравнение вида
, то имеем уравнение вида  .
.
Решим три уравнения:
1) ,
,  , откуда
, откуда 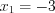 ,
,  ;
;
2) , откуда
, откуда  , тогда
, тогда 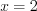 или
или  , тогда
, тогда  ;
;
3) , откуда
, откуда  . Выполним проверку: подставим значение
. Выполним проверку: подставим значение  в исходное уравнение и получим
в исходное уравнение и получим  . Так как имеем неопределенность вида
. Так как имеем неопределенность вида 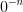 , то число
, то число  не является корнем исходного уравнения.
не является корнем исходного уравнения.
Уравнение имеет три корня:
имеет три корня: 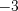 ;
;  и
и  .
.
Ответ: .
.
 , то имеем уравнение вида
, то имеем уравнение вида  .
. Решим три уравнения:
1)
 ,
,  , откуда
, откуда 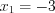 ,
,  ;
; 2)
 , откуда
, откуда  , тогда
, тогда 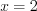 или
или  , тогда
, тогда  ;
; 3)
 , откуда
, откуда  . Выполним проверку: подставим значение
. Выполним проверку: подставим значение  в исходное уравнение и получим
в исходное уравнение и получим  . Так как имеем неопределенность вида
. Так как имеем неопределенность вида 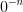 , то число
, то число  не является корнем исходного уравнения.
не является корнем исходного уравнения. Уравнение
 имеет три корня:
имеет три корня: 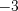 ;
;  и
и  .
. Ответ:
 .
.Если уравнение имеет вид  , то его решение образуют корни уравнений:
, то его решение образуют корни уравнений:
 , то его решение образуют корни уравнений:
, то его решение образуют корни уравнений: 1)  при
при 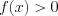 и
и  ;
;
 при
при 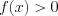 и
и  ;
; 2) 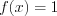 ;
;
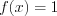 ;
; 3)  .
.
 .
. Заметим, что необходимо выполнить проверку корней уравнения  , так как, подставив полученные числа в уравнение
, так как, подставив полученные числа в уравнение  , можем получить неопределенность вида
, можем получить неопределенность вида 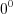 или
или  .
.
 , так как, подставив полученные числа в уравнение
, так как, подставив полученные числа в уравнение  , можем получить неопределенность вида
, можем получить неопределенность вида 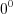 или
или  .
. Случай, когда 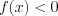 , нами не рассматривается.
, нами не рассматривается.
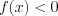 , нами не рассматривается.
, нами не рассматривается. 






 .
. и применим свойство
и применим свойство