Модулем (абсолютной величиной) числа  называют число
называют число  , если
оно неотрицательное, и противоположное ему число, если число
, если
оно неотрицательное, и противоположное ему число, если число  отрицательное:
отрицательное:  , если
, если  и
и  , если
, если  .
.
Следовательно, модуль любого числа – величина
неотрицательная.
Методы решений уравнений
 , (5.11) то:
, (5.11) то: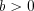 оно равносильно совокупности уравнений
оно равносильно совокупности уравнений  (5.11.1)
(5.11.1) оно равносильно уравнению
оно равносильно уравнению  ; (5.11.2)
; (5.11.2) не имеет решений.
не имеет решений. (5.12)
(5.12) и
 , то оно равносильно совокупности уравнений:
, то оно равносильно совокупности уравнений: ![\[ \left[ \begin{aligned} f(x)=g(x),\\ f(x)=-g(x). \end. \] LaTeX formula: \[ \left[ \begin{aligned} f(x)=g(x),\\ f(x)=-g(x). \end. \]](/uploads/formulas/1be506d13946340fa1db61227dae4733b865f53a.1.1.png) (5.12.1)
(5.12.1)  , (5.13)
, (5.13) то оно равносильно неравенству
 . (5.13.1)
. (5.13.1) , (5.14)
, (5.14) то оно равносильно уравнению
 . (5.14.1)
. (5.14.1)5. Если уравнение
содержит несколько модулей, например, имеет вид
 , (5.15)
, (5.15)
то применяем метод интервалов:
1) найдем нули функций, стоящих под знаками
модулей, решая уравнения  и
и  ;
;
2) нанесем нули функций на область определения
уравнения;
3) раскроем модули на каждом из полученных
промежутков;
4) решим полученные уравнения;
5) отберем корни на каждом промежутке, оставляя
корни, принадлежащие рассматриваемому промежутку.
Записывая промежутки, граничные
точки будем включать в промежуток только один раз, например при первом их
упоминании.
 .
. , уравнение запишем в виде:
, уравнение запишем в виде:
По теореме, обратной теореме Виета, получим:
 , тогда
, тогда  или
или  , тогда
, тогда  .
. Найдем квадрат произведения корней уравнения:
 .
. Ответ:


 .
.Следовательно,




откуда по теореме, обратной теореме Виета,
 .
. Ответ:
 .
. .
. равносильно 5.11.1, при
равносильно 5.11.1, при  равносильно 5.11.2, а при
равносильно 5.11.2, а при  решений не имеет. Следовательно,
решений не имеет. Следовательно, 
![\[ \left[ \begin{aligned} \left || x-5 \right |-5|=10,\\|| x-5 |\right |-5|=0; \end. \] LaTeX formula: \[ \left[ \begin{aligned} \left || x-5 \right |-5|=10,\\|| x-5 |\right |-5|=0; \end. \]](/uploads/formulas/89b70638c4aaba6072ab42534b436e1bbd17ca5f.1.1.png)
![\[ \left[ \begin{aligned} & \ \left | x-5 \right |-5=10,\\ & \ \left | x-5 \right |-5=-10, \\ & \ \left | x-5 \right |-5=0; \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ \left | x-5 \right |-5=10,\\ & \ \left | x-5 \right |-5=-10, \\ & \ \left | x-5 \right |-5=0; \end. \]](/uploads/formulas/c7b0d2d14296a537cf0ab770b4ed6c8df6e2a65f.1.1.png)
![\[ \left[ \begin{aligned} & \ \left | x-5 \right |=15,\\ & \ \left | x-5 \right |=-5, \\ & \ \left | x-5 \right |=5; \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ \left | x-5 \right |=15,\\ & \ \left | x-5 \right |=-5, \\ & \ \left | x-5 \right |=5; \end. \]](/uploads/formulas/a6751cb82e7def51f8137dda12c7cf73e9b0157a.1.1.png)
![\[ \left[ \begin{aligned} & \ x-5=15,\\ & \ x-5=-15, \\ & \ x-5=5, \\ & \ x-5=-5; \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ x-5=15,\\ & \ x-5=-15, \\ & \ x-5=5, \\ & \ x-5=-5; \end. \]](/uploads/formulas/3a1df93309ead642819b0be13ec92085798f621a.1.1.png)
![\[ \left[ \begin{aligned} & \ x=20,\\ & \ x=-10,\\ & \ x=10,\\ & \ x=0. \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ x=20,\\ & \ x=-10,\\ & \ x=10,\\ & \ x=0. \end. \]](/uploads/formulas/b021e680dd2c9e492371c6c18e3a0008d67890f3.1.1.png)
Ответ:
 .
. .
.![\[ \left[ \begin{aligned} & \ x^2-4x-2=4x+18,\\ & \ x^2-4x-2=-4x-18; \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ x^2-4x-2=4x+18,\\ & \ x^2-4x-2=-4x-18; \end. \]](/uploads/formulas/126be8be5d2ff0bf5a3ed1cd50e8b9f0801befce.1.1.png)

![\[ \left[ \begin{aligned} & \ x^2-8x-20=0,\\& \ x^2=-16; \end. \] LaTeX formula: \[ \left[ \begin{aligned} & \ x^2-8x-20=0,\\& \ x^2=-16; \end. \]](/uploads/formulas/f6351f98f8b1a96a9c8b8a19755a80c877516326.1.1.png)

 .
. Ответ:
 .
. .
.Найдем нули функций, записанных под знаками модулей, решая уравнения:
1)
 , откуда
, откуда  ;
; 2)
 , откуда
, откуда  .
. Нанесем числа
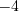 и
и  на координатную прямую (рис.5.5).
на координатную прямую (рис.5.5). Рассмотрим полученные промежутки и раскроем модули на каждом из них.

![(-\infty ;-4] LaTeX formula: (-\infty ;-4]](/uploads/formulas/fefcd9791b222aedef1c95c26da13f92fc87732a.1.1.png) данное уравнение примет вид:
данное уравнение примет вид: или
или  .
. Следовательно, любое число, принадлежащее промежутку
![(-\infty ;-4] LaTeX formula: (-\infty ;-4]](/uploads/formulas/fefcd9791b222aedef1c95c26da13f92fc87732a.1.1.png) , является решением уравнения.
, является решением уравнения.![(-4 ;6] LaTeX formula: (-4 ;6]](/uploads/formulas/6b9f8fe5a63e6f30d3651aa67f901ea9b00551b5.1.1.png) получим:
получим:  .
. Поскольку число
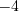 не принадлежит промежутку
не принадлежит промежутку ![(-4 ;6] LaTeX formula: (-4 ;6]](/uploads/formulas/6b9f8fe5a63e6f30d3651aa67f901ea9b00551b5.1.1.png) , то оно не является решением уравнения на этом промежутке.
, то оно не является решением уравнения на этом промежутке. получим:
получим: или
или  .
. Следовательно
 .
. Ответ:
![(-\infty ;-4] LaTeX formula: (-\infty ;-4]](/uploads/formulas/fefcd9791b222aedef1c95c26da13f92fc87732a.1.1.png) .
. ;
; .
.


